対数を使った二項分布の計算について　~D.N. mini~ vol 2

今回は以下の記事で取り扱っている二項分布について説明したいと思います。

1. 二項分布とは？

　まず、二項分布について少し復習しましょう。二項分布は、以下の条件を満たす試行に関する確率分布の一つ

• 試行が独立であること。

• 各試行が成功か失敗のどちらかに分類できる（成功確率をp、失敗確率をq = 1 - pとします）こと。

• 試行回数が固定されていること。

　この３つの状況で、n回の試行のうち、k回成功する確率を求めるというのが二項分布です。

二項分布の確率関数は以下の式で表せられます。

ここで、（ｎ,ｋ）は二項係数と呼ばれるやつ（nCkとも言われます）。

---

2. 二項分布を計算する際の問題点

　試行回数 n や成功確率 p が小さかったり大きかったりすると・・・直接、この式を計算するのは難しくなるんです。たとえば、大きな数の階乗（n!）はすぐにとても大きな数になるため、コンピュータで扱うとオーバーフローのリスクがあります。

　また、極端に小さな確率（例えば、非常に低い排出率）をそのまま扱ってしまうと、アンダーフロー（数値が非常に小さくなりすぎてゼロになってしまう）が発生します。

---

3. 対数を使った二項分布の計算

　そこで、これらの問題を回避するために、対数を使って計算する方法があります。対数を使うことで、大きな数を扱いやすくし、さらに掛け算や割り算を足し算と引き算に変換できるという利点があります。

まず、二項係数の対数を計算します。通常の二項係数は以下の式で表されます：

これを対数に変換します。対数の性質を使うと、以下のように展開できます。

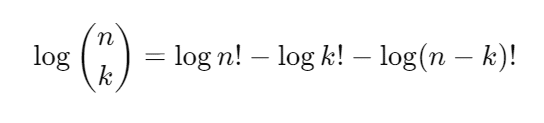
　これで、掛け算や割り算という計算から、足し算や引き算という計算を手に入れました。

---

5. 全体の計算式

　ここまでで得られた対数を使った二項分布の確率を計算する全体の式は次のようになります。

ここで、まず二項係数の対数を計算し、その後、成功確率 ｐ＾ｋ（ｐのｋ乗） と失敗確率 (１-ｐ)＾(ｎ-ｋ) の対数を加算します。

最終的な確率 P(X=k)を得るには、計算された対数の結果を指数関数で元に戻します。

これで大きな数でも近似できる。よかった！！！！！！

---

6. 実際の活用例

　これを実際のコードに落とし込んだ例が以下のようになります

function logFactorial(n) {
    if (n === 0 || n === 1) return 0;
    let result = 0;
    for (let i = 2; i <= n; i++) {
        result += Math.log(i);
    }
    return result;
}

function binomialCoefficientLog(n, k) {
    return logFactorial(n) - logFactorial(k) - logFactorial(n - k);
}

function binomialProbability(n, k, p) {
    const logP = binomialCoefficientLog(n, k) + k * Math.log(p) + (n - k) * Math.log(1 - p);
    return Math.exp(logP);
}

---

最後に

　このように、対数を使った階乗や二項係数の計算によって、非常に大きな数や小さな数を安全に扱いながら、確率計算などを効率的かつ正確に行うことができます。

　これでガチャを１００回や２００回回しても計算できるようになり、つまるところ世間が許す限り回し続けることができると。でも、当たるまで回せばいくらだろうが問題ないんで・・・・・・まあ意味ないですね。

---