
新しい素数見つかったって!!~D.N. mini~ vol 2
はじめに
新しい素数が2024年10月に発見されました!これは「メルセンヌ素数」と呼ばれる特別な種類の素数で、2のべき乗から1を引いた形 2^{136,279,841}−1 をしているそう。
この数はなんと約4,102万桁もあり、これまでの記録を16万桁以上も上回った、すごい。今回の発見は、Great Internet Mersenne Prime Search (GIMPS) というプロジェクトによって行われ、GPUクラウドコンピューティングの力を借りて計算されたもの。
このような超巨大な素数の発見には、数千台のコンピュータが協力し、膨大な時間と計算リソースを費やして検証されます。今回の発見もその例であり、数十カ国のボランティアが集まってこの計算を支えました。
もし興味があれば、これをみているあなたもGIMPSプロジェクトに参加して、次の巨大素数の発見に貢献することができるらしい。
1. メルセンヌ素数って何?
メルセンヌ素数は、特別な形をした素数の一種で、次のように表される。
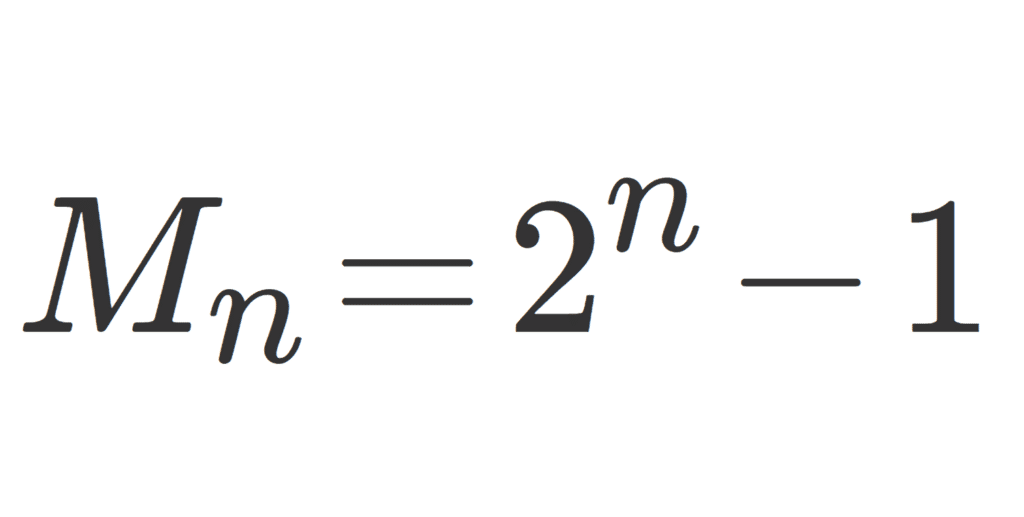
ここで、nは自然数。例えば、23−1=72^3 - 1 = 723−1=7はメルセンヌ素数の一例で、nが素数であるときに限って、メルセンヌ数自体も素数である可能性が高いそう。でも、全てが素数になるわけではないから注意が必要。
2. 最新の発見:
2024年に発見された最新のメルセンヌ素数は、2^{136,279,841} −1で、なんと約41.02万桁にもなる巨大な数!これまで見つかったメルセンヌ素数の中でも、過去の記録を大幅に上回る大きさ!
この数を見つけたのは、GIMPS(Great Internet Mersenne Prime Search)というプロジェクト。世界中のボランティアがコンピュータを使って参加して、協力しながら素数を探している。今回は、GPUを使ったクラウドコンピューティングの技術を駆使して見つけられた。
3. どうやって発見されたの?
巨大な素数を見つけるためには、膨大な計算が必要で、そのために数千台のコンピュータが並列に計算を行うんだ。メルセンヌ素数をチェックするには、LLR(Lucas-Lehmer primality test) というテストを使う、これが素数かどうかを判定するための非常に効率的なアルゴリズムなんだそうな。
4. なぜ素数が重要なのか?
素数は、暗号技術やデータセキュリティの分野で非常に重要。大きな素数を使うことで、安全性の高い暗号を作ることができる。例えば、RSA暗号などは素数の特性を使っていて、特にこのような巨大な素数は、現代のインターネットセキュリティの根幹を支えている。
5. どうして発見するのが難しいの?
素数の特性上、簡単には見つからない。普通の数に比べて、素数は計算が非常に難しく、特にメルセンヌ素数のような超巨大素数になると、計算リソースや時間が莫大にかかる。だからこそ、GIMPSのようなプロジェクトで世界中のコンピュータの力を合わせて探してる。
まとめ
最新のメルセンヌ素数の発見は、数学やコンピュータ技術の限界を押し広げるめちゃくちゃすごい出来事。GIMPSプロジェクトみたいに、世界中の力を集結して巨大な数を探索するなんて、まさに現代ならではの挑戦といえる。
計算リソースと高度なアルゴリズムを駆使して、何百万桁もある素数を見つけ出すのはとても驚異的。素数は暗号技術にも不可欠で、日常生活やインターネットの安全性にも影響を与えている。
すごい!感動した!!素数ってさ、何千回計算しても出てこないときあるけど、ひとたび出てきたら『ああ、この数字だけは特別だ!』って気づく。
でも、人間関係でも同じかも…特別な人ってなかなか見つからないけど、見つけたら本当に貴重なんじゃない!?そして!今、大切な人がいる君もまた、誰かの「素数」なんじゃないか?
ん???????

