Tesla株を時系列解析と機械学習を用いて予測してみた

R N

はじめに


ChatGPTのOpenAIの共同創業者でもある常に話題の人物イーロン・マスク（※超尊敬）。彼が経営する電気自動車メーカーのTeslaの株価は先月に急落しましたが、以前のように再度急騰する未来は来るのでしょうか？そんな考えから、株価を予測したいと思い、この度Teslaの株価を時系列解析を用いて分析、予測することにしました（※株価予測を本気で行う場合、個別銘柄であればアルファを予測するなどそもそもドメイン知識が必須であったり、本分析が適切か否かといった声が上がりそうなので、あくまで本投稿は投資を目的としたものではなく、データ分析の学習の一環としております。ご了承ください。また、本記事は〜初学者にご理解していただけるよう、簡単に解説も交えていきます）。

まず、大前提の話ですが、データを分析する上で最も重要だといっても過言でないことは、「データの可視化」です。
データ分析は、収集することがゴールではなく、収集したデータを整理し把握してから、初めてデータの分析を行う事ができます。そして、考察を深めたり、様々なテストを行ったりすることで、データ分析をする理由、つまり「データを分析しようと思った何かしらの目的」に繋がる価値を見出すことができるのです。その為には、自身を含む考察する誰しもが直感的に分かりやすいよう「データを可視化する」ことが重要です。

その上で、データの可視化をどのように行うかというと、今回は時系列解析を採用します。
時系列解析とは、時系列データを使用した分析で、株価予測以外にも売上予測や来客予測などにも使用されます。

それでは、実際の分析手順とそれぞれをセクション毎に解説してきます。

  1. データの読み込み（取得）

  2. データの整理（前処理）

  3. データの可視化

  4. 時系列解析の手法を用いたデータ分析

  5. 結果に対する考察

※実行環境：今回は環境構築が必要な為、GoogleのColaboratoryを使用しています。
※機械学習の手法：時系列分析のSARIMAモデルを使用しています。

【1. データの読み込み（取得）】


まず、必要なライブラリをインポート、加えて必要なデータを取得します。今回はYahoo! Financeを使用します（https://pypi.org/project/yfinance/）。

import warnings
import itertools
import numpy as np
import missingno as msno
import matplotlib.pyplot as plt
import pandas as pd
import statsmodels.api as sm
import yfinance as yf
from multiprocessing import Pool

# 1. データの取得
# 1-1. yfinance（Yahoo Financeから金融データを取得するためのライブラリ)からPandasのデータフレーム型でTesla株価データを取得。
df = yf.download("TSLA")

print(df)
取得したデータ

【2. データの整理（前処理）】


今回は終値から株価予測を行う為、取得したデータの不要な列（column）は、削除します。

# 2. データの整理（前処理）
df = df.drop(["High", "Low", "Adj Close", "Open", "Volume"], axis=1)

print(df)


整理したデータ

【3. データの可視化】


ここで元データを直感的にも分かりやすくする為に、一度可視化してみます。

元データ（原系列）

とっても分かりやすくなりましたね！これがいわゆる「可視化」です。
数値で出力することも、折れ線グラフにすることも全て可視化ですが、できる限り直感的に分かりやすくする可視化が分析する上では重要ですね。

さて、本来であれば、データの前処理やデータクレンジングと言われるデータの準備が大変なケースが多く、外れ値の除去や欠損値への対応などが必要とされます。ですが、今回使用するyfinanceはありがたいことにデータが既に綺麗に整理されているので、特別な前処理を行わずに次に進もうと思います。

とはいえ、前処理はとても大切です。分析を行う以前の問題である前処理は、本来であればとっても大変なのです。
大前提、時系列分析においてはデータを分析する際、定常性のある時系列データにする必要があります。定常性とは、時系列データの統計的な性質が時間によらず一定であることを指します。これが重要な理由は、定常性がないデータを分析すると、意味のない相関を検出してしまう可能性があるからです。

例えば、テスラの株価で考えてみます。時間が経過するにつれて、テスラの株価は変動します。同時に、時間が経つと、例えば世界の電気自動車の販売台数も増えていくかもしれません。しかし、「電気自動車の販売台数が増えたからテスラの株価が上がった」と結論づけるのはナンセンスかもしれません。なぜなら、「テスラの株価が上がった」と「電気自動車の販売台数が増えた」の両方の事象は、原因が「時間の経過」である可能性があるからです。

このように、定常性がないデータをそのまま分析すると、本当の因果関係を見誤る可能性があります。そのため、時系列解析を行う際には、まずデータの定常性を確認し、必要に応じて差分を取るなどして定常性を持たせる前処理が必要となります。

では、今回使用するデータは定常性があると感じますか？恐らくあまり一定ではなく、少し複雑に感じるかと思います。そう感じた場合、その感覚は正しく、このような一見複雑で様々特徴がありそうな時系列データは、定常性のある時系列データにしていく必要があります。

また、時系列データには、トレンド、季節変動などの周期変動、不規則変動の３つのパターンが隠れています。この隠れたそれぞれのパターンから分析を行い、様々な特徴を見出すことが、時系列解析です。
そしてその為には、モデルを構築するモデリングという作業をする必要があり、モデリングをする為には時系列データにどのような特徴があるか調べる必要があるため、前処理したデータを多角的に分析してみる必要があるのです。

そこで、本データを定常性のあるデータにできないか、データの性質を視覚的にわかるように原系列、トレンド、季節変動、不規則変動（残差）に分けて、それぞれ視覚的に確認してみようと思います。

※period=21について、今回使用する株価データはデイリーで、週5営業日の周期となっています。つまり、1か月を約21営業日とし、本数字としています。また、52としているのは、1年間を約52週としている為です。
※わかりやすいよう、約1年間分のデータのみ可視化します。

# 原系列、トレンド、季節変動、不規則変動（残差）と、それぞれ比較できるよう可視化
# 月間
fig_month = sm.tsa.seasonal_decompose(df[2995:], period=21).plot()
plt.show()

# 年間
fig_year = sm.tsa.seasonal_decompose(df[2995:], period=52).plot()
plt.show()
月間：上から原系列、階差系列（トレンド）、周期変動、不規則変動（残差）
年間：上から原系列、階差系列（トレンド）、周期変動、不規則変動（残差）

上記から、この原系列データにはトレンド、季節変動含む周期変動、不規則変動がそれぞれある事が確認できました。

ですが、まだ定常性のあるデータには辿り着いていません。ここからデータ分析ができるよう、本来であればトレンドと季節変動を取り除き、定常化したデータにしたいと思いますが、それらだけでは結論難しいので、一つ一つ確認だけしていこうと思います。

それではまず、対数変換を行い、データの変動を穏やかにし、自己共分散を一様にします（めちゃくちゃざっくり言うと異なるデータ同士がどの程度関連しているか）

# 対数変換して可視化
df_log = np.log(df)
plt.title("Tesla Chart Data LOG")
plt.xlabel("date and time")
plt.ylabel("closing price")
plt.plot(df_log)
plt.show()
原系列を対数変換

上記のように対数変換しただけでは、定常化には辿り着きません。

次に、移動平均（簡単に言うと平均値）を行います。これによって例えば12個の連続する移動平均を求めることで、季節変動を除去し、トレンド成分を抽出する事ができるかもしれません。

# 移動平均を行って可視化（月間）
# 原系列のグラフ
plt.subplot(3, 1, 1)
plt.title("Tesla Chart Data")
plt.xlabel("date and time")
plt.ylabel("closing price")
plt.plot(df)

# 移動平均のグラフ
df_avg = df.rolling(window=21).mean()
plt.subplot(3, 1, 2)
plt.title("Tesla Chart Data MEAN")
plt.xlabel("date and time")
plt.ylabel("closing price")
plt.plot(df_avg)

# 原系列-移動平均グラフ
plt.subplot(3, 1, 3)
plt.title("Tesla Chart Data MOV_DIFF")
plt.xlabel("date and time")
plt.ylabel("closing price")
mov_diff_df = df - df_avg
plt.plot(mov_diff_df)

plt.tight_layout()

plt.show()
上から原系列、移動平均、原系列-移動平均（月間）
# 移動平均を行って可視化（年間）
# 原系列のグラフ
plt.subplot(3, 1, 1)
plt.title("Tesla Chart Data")
plt.xlabel("date and time")
plt.ylabel("closing price")
plt.plot(df)

# 移動平均のグラフ
df_avg = df.rolling(window=52).mean()
plt.subplot(3, 1, 2)
plt.title("Tesla Chart Data MEAN")
plt.xlabel("date and time")
plt.ylabel("closing price")
plt.plot(df_avg)

# 原系列-移動平均グラフ
plt.subplot(3, 1, 3)
plt.title("Tesla Chart Data MOV_DIFF")
plt.xlabel("date and time")
plt.ylabel("closing price")
mov_diff_df = df - df_avg
plt.plot(mov_diff_df)

plt.tight_layout()

plt.show()
上から原系列、移動平均、原系列-移動平均（年間）

見ての通り、先ほどよりは定常化に近づいていますが、まだまだ定常性があるデータとは言いにくです。

階差系列への変換はどうでしょうか？ちなみにこの方法が最も一般的な方法で、トレンドと季節変動を同時に除去する事ができます。

# 階差をとる
plt.subplot(2, 1, 2)
plt.title("Tesla Chart Data DIFF")
plt.xlabel("date and time")
plt.ylabel("closing price")
df_diff = df.diff()
# 階差系列のプロット
plt.plot(df_diff)

plt.tight_layout()

plt.show()
上から原系列、階差系列

（くそう。。）では、季節変動を取り除けばどうでしょうか？原系列 - トレンド - 季節変動 = 残差となり、残差が定常性のある時系列データに近づいていくはずです。

# 季節調整とグラフのプロット
res = sm.tsa.seasonal_decompose(df, period=52)
fig = res.plot()
plt.show()
上から原系列、階差系列（トレンド）、周期変動、不規則変動（残差）

上記は冒頭でも同様のことを実行しましたが、ここまでで分かったようにこのデータは階差と周期変動を除去した残差は定常とは言い難い状態です。
よく見ると外れ値がある可能性があるので、外れ値があるか可視化して確認していきます。

# 外れ値の可視化（分かりやすいようにインデックスである日時データをcolumnに変更しています）
df = df.reset_index()
print(df.columns)

sns.boxplot(y=df["price"])
plt.show()

sns.jointplot(x=df['day'], y=df['price'], data=df)
plt.show()
boxplotによる外れ値確認
jointplotによる外れ値確認

これにより直感的に外れ値が存在していることが確認できるかと思います。

では、外れ値を外していけないかも試してみます。まずは本データの平均値（μ）または期待値（E[x]）、分散（Var[x]）、ボラティリティを意味する標準偏差（σ）を確認します。

# データの平均値、分散、標準偏差
# 上記でcolumnが["Date"]と["Close"]になっているので、["Date"]をindexに変更します
df = df.set_index('Date')
mean_value = df.mean(axis=0) # 平均値の計算
var_value = df.var(axis=0)  # 分散の計算
std_value = df.std(axis=0)  # 標準偏差の計算

print("平均値:", mean_value)
print("分散:", var_value)
print("標準偏差:", std_value)
終値の平均値=62.253653 / 分散=9258.387468 / 標準偏差=96.220515

次に相関係数（過去の値とどれほど似ているか）を確認していきます。

終値の自己相関係数

加えて、ホワイトノイズ（時点tによって発生するランダムな値で、不規則変動(残差)パターンを示す）を確認します。

 #ホワイトノイズの設定 
mean = 62 # 平均値(通常は0)
std = 96 # 標準偏差(通常は1)
num_samples = 3247 #データポイント数 
samples = np.random.normal(mean, std, size=num_samples)
# ホワイトノイズのプロット
plt.title("Whitenoise")
plt.plot(df)
plt.show()
※終値のホワイトノイズからも定常性がないと確認できます。


これらから分かるように、本来であればデータの差分を取って定常化し予測や分析を行うことができればいいのですが、なかなか難易度が高そうです。

ここで諦め、、というわけにはいきません！

そこで！大変便利なモデルを用いようと思います。それが、SARIMAモデルです。

ARモデル（自己回帰モデル：過去の値から回帰的にある地点の値を予測し、規則的に値が変化する）とMAモデル（移動平均モデル：過去の誤差に影響され、影響される値までは自己相関を持つ）を組み合わせたARMAモデル（ARモデルとMAモデルの組み合わせ）というものが存在します。このモデルは、定常過程、つまり定常性のあるデータにしか通用しませんが、非定常過程、つまり定常性がないデータの平均や分散が時間に依存しているデータにも通用できるARIMAモデルというARMAモデルの発展版があります。そして、そのARIMAモデルを季節周期を持つ時系列データにも対応できるようにしたモデルが、SARIMAモデルです。

【4. 時系列解析の手法を用いたデータ分析】


これからそのSARIMAモデルを用いて、株価分析を行いますが、SARIMAモデルには、
・p（自己相関度：モデルが直前q個の値を用いているか）
・d（誘導：時系列データを定常にするためのd次の階差）
・q（移動平均：モデルが直前q個の値に影響を受けていること）
・s（周期：季節変動の値s）
・sp（s * p）
・sd（s * d）
・sq（s * q）
と、7つのパラメータが存在します。
パラメータとはモデル内部の変数で、通常データから学習されますが、Pythonには自動で最も適切にしてくれる機能は存在しません。
そのため、情報量基準と言われるどの値が最も適切なのか調べるプログラムを書く必要があります。
情報量基準はいくつか種類がありますが、今回はベイズ情報量基準（BIC）と呼ばれるものを使います。この情報量基準では、BICの値が小さいほどモデルの予測力とパラメータ数のトレードオフが良いことを示します（本コードの詳細はコメントアウトで記述します）。

# 情報量基準のベイズ情報量基準（BIC）のプログラムを作成
def calc_bic(params):
    # param = パラメータであるpもしくはdもしくはqを指しています。param_seasonalはsp、sd、sqです。
    param, param_seasonal = params
    try:
        # sm.tsa.statespace.SARIMAXを使用してARIMAモデルを作成。
        mod = sm.tsa.statespace.SARIMAX(df, order=param, seasonal_order=param_seasonal)
        # 変数resultsにモデルを適合
        results = mod.fit()
        # 返り値として該当のモデルのBIC値と該当の各パラメータをリストとして指定
        return [param, param_seasonal, results.bic]
    except:
        # もしエラーが起きた場合には無限大の値を意味するnp.infと該当のパラメータをリストとして返す
        return [param, param_seasonal, np.inf]

# p, d, qの範囲を0~1に指定
p = d = q = range(0, 2)
# itertools.productを用いてp、d、qの全ての組み合わせをリスト型で変数pdqに格納
pdq = list(itertools.product(p, d, q))
# 影響を受ける周期sは21、つまり1ヶ月毎とし、itertools.productを用いてp、d、qとsp、sd、sq、加えてsの全ての組み合わせをリスト型で変数seasonal_pdqに格納
seasonal_pdq = [(x[0], x[1], x[2], 21) for x in list(itertools.product(p, d, q))]

# with文を用いてmultiprocessingモジュールのPoolで複数のプロセスを同時に並列化（※ 計算時間圧縮の為）
with Pool(4) as p:
    # map関数を用いて、itertools.productを用いてpdqと seasonal_pdqの全ての組み合わせをリスト型で返し、その返り値を全て関数calc_bicの引数に当てはめ実行し、変数resultsに返す
    results = p.map(calc_bic, list(itertools.product(pdq, seasonal_pdq)))

# 最適なパラメータ（lamdbaによりx[2]つまり、resultsの値（リストなので、各要素）となる[param, param_seasonal, BIC]の内、3番目であるBIC値の最小値）を選択
best_params = min(results, key=lambda x: x[2])

print(best_params)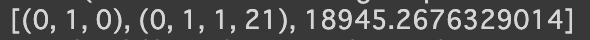
best_paramsの出力結果

上記のような結果となったので、この値をSARIMAモデルに当てはめます。

# モデルの当てはめ
SARIMA_df = sm.tsa.statespace.SARIMAX(df,order=best_params[0],seasonal_order=best_params[1]).fit()

そして、SARIMAモデルを用いて予測データを作成し、プロット、表示します。

# predに予測データを代入する 
pred = SARIMA_df.predict("2020-05-19", "2023-05-19")

# 元の時系列データと予測データ(pred）の可視化 ※分かりやすいように予測データは赤で表示
plt.plot(df)
plt.plot(pred, color="r")
plt.show()
青：元データ（原系列） / 赤：予測データ

元データとほぼズレない結果となりました。

【5. 結果に対する考察】


今回の分析では、一見綺麗な予測結果となっていますが、BIC値があまりにも高かったので、AICを情報量基準で選定することや他の要因を考慮に入れたマルチファクターモデルの導入、さらにはディープラーニングを用いた予測モデルの構築など行いたいと思います。

また、時系列データのみでの株価予測は単なるランダムウォークに等しい為、そもそもではありますが適切な株価の分析を行うことは難しいはずです。

最後簡単になってしまいましたが、データ分析はやり始めると止まらないくらい面白いものなので、少しでも理解を深めるもしくは興味を持たれる方がいれば幸いです。

、、それでは！！


この記事が気に入ったらサポートをしてみませんか？