
有用な対称性に基づかないダイナミカルな保存則
古典力学でも量子力学でも、系が持つ対称性を起源とする保存則は重要な意味を持っています。その対称性の変換の生成子となる電荷は、ネーターの定理によって時間変化しないことが証明されているのです。例えば球対称性をもつ系ではネーターの保存電荷として角運動量が得られます。一方で、各時刻ごとにその定義式が変わっていくダイナミカルな保存電荷の存在も知られています。この保存則の物理的な起源は、状態の時間発展が作る軌道達がいつまでも決して交差をしないという性質にあります。
まずは古典解析力学で考えてみます。一般にハミルトニアンは下記のように時間に陽に依存しても構いません。それでも保存電荷を構成することができます。

このハミルトニアンに対応する正準方程式は(2)式で与えられます。

この解は、時刻t=0での位置座標xと運動量座標pの初期値を決めれば、一意に定まります。そして2つの異なる初期値に対しての、解の相空間中の時間発展の軌道は決して交差しないことが、この正準方程式から保証をされています。この性質が重要です。
各時刻で決して軌道は交差しない(特定の点に2つの軌道は存在しない)ため、各軌道にそれぞれ適当な実数を一意に割り振ることが可能です。図1では異なる3つの軌道のそれぞれに、異なる電荷Qの値を割り振っています。

図1では時間発展のそれぞれの軌道にQの値が対応しているのですが、一方で各時刻での相空間上の関数としてQを捉えることも可能です。ただしそうやって定義をされたQは、xとpだけでなく、一般にはtにも依存します。時々刻々とQの定義式自体が時間変化をするので、このQはダイナミカルな保存量と呼ばれます。一方、回転対称性が起源の角運動量などのネーター保存電荷は、各時刻においてその定義式に時間依存性はありません。
このダイナミカルな電荷の保存則の存在は、正準変換からも理解できます。まず時刻tでの(2)式の解は、時刻t=0での座標からの変換になっています。それを(3)式のように書いてみましょう。

正準方程式である(2)式の構造から、(3)式の変換は下記の性質を満たすことが保証されます。

これはポアソン括弧式が1であることを意味していますので、時刻tの相空間の座標と、t=0の相空間の座標は正準変換で繋がっているのが、(5)式のように確認できます。

また(3)式の逆変換を(6)式のように書いてみましょう。この変換も1対1写像になっています。

すると(2)式から同様に

という性質が証明できます。ですので時刻tの座標からt=0への変換でも、(8)式のポアソン括弧式を満たしています。

ダイナミカルな保存電荷Qを各時刻tで定義したければ、一旦t=0へと正準変換をして、その位置と運動量の初期値に関する任意の関数としてQを定めれば良いのです。その後に元の時刻tへの逆正準変換をすることで、各時刻でのQの定義式を得ることができます。
結局ここでやっていることは、ハミルトン=ヤコビの方法で時刻tと時刻t=0を結ぶ正準変換を求める以上のことは何もしていません。その意味でダイナミクスを敢えて保存則という言語で表現しただけとも言えます。
このような構成でQを作れば、どんな時間依存性を持ったハミルトニアンの系でも、対称性に依存せずに保存電荷を構成することができます。例えば図2のように、ある有限時間領域にだけ位置に依存した電場が現れる時空においての荷電粒子の運動にも、そのようなダイナミカルな保存則を導入することが可能となります。

止まっていた荷電粒子が電場によって加速した後でも、上の構成法によってある量が加速前と同じであることが導かれます。
また(9)式のような時間依存性をもつハミルトニアンを持った量子系においても、同様にダイナミカルな保存電荷を導入することはいつでもできます。

この時間発展はユニタリ変換を用いて(10)式のように書けます。
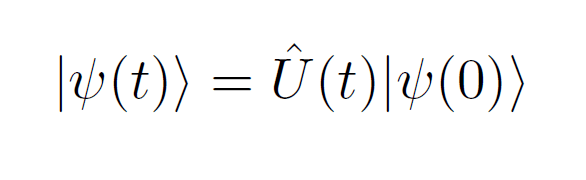
このユニタリ変換を使って、ダイナミカルに保存する電荷Qのシュレディンガー演算子を(11)式で定義しましょう。
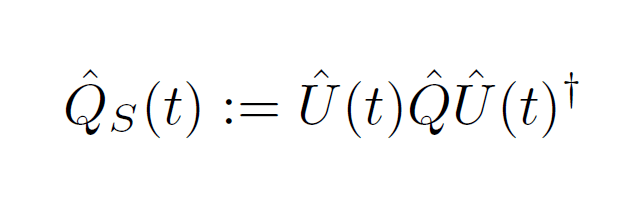
すると当たり前ですが、そのハイゼンベルグ演算子は(12)式のように時間依存性が無くなります。

従って自明にQは時間変化をしない保存電荷になっています。

このように古典力学でも量子力学でも、ダイナミカルな保存則はいつでも導入できます。ただ繰り返しますが、それは状態の時間発展の軌道が交差をしないという数学的な構造だけから得られているものであり、物理のダイナミクスの詳細に関わっているわけではありません。その意味でエネルギーや運動量、角運動量などの保存則に比べて、Qの時間非依存性が持っている情報はとても少ないとも言えます。物理学に出てくる保存則には、このようにいろいろと種類があるのです。
追記(2024/8/15):渡辺さん@haruki_wtnbと、のこさん@NOCO_1002との議論に基づいて、「ダイナミカルな電荷は対称性に基づかない」という内容を含む部分を修正しました。このnoteのように、正準変換で時刻tの位置と運動量を初期時刻の位置と運動量と時刻tの関数で書いてその逆正準変換を考えれば、時間に依存したどんな複雑なハミルトニアンの系でも保存する電荷を構築することができます。その電荷の定義式は一般には時間に露わに依存したものですが、その電荷が生成子となる正準変換に対して作用は不変になります。この意味では上の方法でどんな系に対しても構成できる電荷もネーター電荷になっています。
いいなと思ったら応援しよう!

