自己重力系の負の比熱

量子力学で学ぶ水素原子の束縛状態では、E=0周辺に無限の縮退が現れます。これは1/rというクーロンポテンシャルが長距離相互作用であるという性質から出てくるものです。この性質のため、統計力学の分配関数やギブス状態の計算が破綻をしています。通常の水素原子は他の物質に囲まれているため、電荷の遮蔽効果のポテンシャルが被さり、この束縛状態の無限縮退の効果は見えなくなります。しかし同じ1/rという振る舞いを持つ重力のニュートンポテンシャルでは、万有引力という性質から、電場のように遮蔽はできません。実際、ニュートンポテンシャルに支配される星の構造の熱力学的な計算や、多数の天体の運動のシミュレーションでは、この長距離相互作用に起因する「負の比熱」という現象が出てきます。熱平衡をもつ普通の系では、温度が高くなるとそのエネルギーも高くなりますが、自己重力系では少数の物体のみに運動エネルギーが集中する配位が優勢になって、そのエネルギー総量は小さいのに、活発な運動をしているその少数の物体の衝突から出てくる光の温度は高くなったりします。一般相対論での自己重力系とも言える蒸発ブラックホールでも、この「負の比熱」が出てくるのは有名です。蒸発するブラックホールはホーキング輻射を出して、そのエネルギーを減少させますが、出てくる輻射の温度はどんどんと高くなります。

分配関数が発散するような場合の本質を見るために、量子的な水素原子から非束縛状態を切り捨てた数理モデルを考えてみましょう。この系のハミルトニアンは下記で与えられます。

ここでエネルギー固有値は角運動量の量子数l,mには依存せず、主量子数nだけに依存をしており、下記の形で与えられます。

なお基底状態のエネルギーが零となるようにエネルギー原点を決めてあります。この系で仮に熱力学の分配関数を、普通のように下記で与えてみましょう。

角運動量の自由度の和をとることで、この分配関数は次のように書けます。

ここで注目する点は、nが無限大となる領域の寄与のために、この分配関数は発散していることです。つまり分配関数がうまく定義できないことを意味しています。そしてこのことは、熱平衡状態を記述する下記のギブス状態も存在していないことも意味しています。

もし無理にこの分配関数やギブス状態を使って、熱平衡状態でのエネルギー期待値を通常の方法で計算をすると

という式に成りますが、敢えてこれを評価すると、エネルギーは温度に依存しなくなり、そしてその期待値はエネルギーの最大値に一致してしまいます。これは物理として変な結果です。

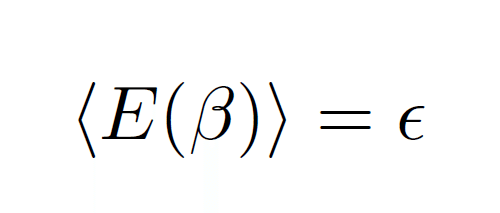
この計算の破綻が意味するのは、このような系に通常の統計力学や熱力学を適用できないという事実です。この系の任意の初期状態から出発をして時間発展を追っても、決して全体的に静的な熱平衡状態に至らないことを意味しているのです。統計力学の計算を正当化するには、状態の典型性が必要となりますが、その典型性が破れているのがこの系の特徴だと言えます。

この事実はブラックホール蒸発でも重要です。負の比熱を示すブラックホールも、厳密な意味では熱力学的な分配関数もギブス状態も持ちません。もし熱平衡状態を作りたい場合には、仮想的な大きな球形の箱を考えて、その中にブラックホールを入れるなどの対応をしています。しかし実際の蒸発過程では、無限遠方まで伝搬していくホーキング輻射を考えて、情報喪失問題などを論じるのが普通です。このことは、ブラックホール蒸発過程にも統計力学での典型性の議論が適用できないことを意味します。例えば典型性を仮定する、ブラックホールと輻射の間のエンタングルメントエントロピーのペイジ曲線も、本当の量子重力理論では実現をしていない可能性が高いのです。この辺りことを、私と共同研究者は下記の論文で論じています。

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.120.181301

水素原子の問題に戻ると、水素原子を箱に入れたり、また外部の電荷による遮蔽効果を考えることで、その分配関数も有限にすることができます。しかし、そのことは長距離領域の境界条件の取り方に物理が非常に依存していることを意味しています。箱にいれて計算すればOKという安易さで物事を見ていると、重要な物理の本質を見失うことも出てくると思います。若い物理学徒の皆さんには、そういう小さな、でも重大な物理が隠れている「ヒント」に敏感になる訓練をして欲しいと願っています。

物理学者は「探偵」です。シャーロック・ホームズのように、人からみれば些細なことを鋭い観察眼で見逃さずに、事件解決へと繋げる名探偵へと成長をして欲しいなぁと願っています。