
量子力学では位置と運動量の足し合わせの量は測れないのか?
前世紀の量子力学勃興期には、測定とは何かという理解が全く不十分な形で、発見論的に様々な現象の説明が試みられていました。散乱断面積や離散準位のエネルギー間隔などは実験データから当時でも読み取れ、それを説明するように量子場まで含めた理論が一気に構築をされました。ただしその過程において、現代で言うところの「量子測定理論」は、素粒子物理や物性物理のコミュニティの中で全く整備もされていませんでした。例えば前世紀の量子力学理論のフロントランナーでもあったユージン・ウィグナーは、何が実験で実際に測られる観測量なのかは明らかではないと述べていたそうです。電子で言えば、その位置xと運動量pは測れると当時も思われていました。しかしウィグナーは、単位を合わせるようにxとpを正の定数倍をした後でそれぞれを足し合わせた下記のようなOという量は観測可能なのか分からないと疑問に思っていたそうです。
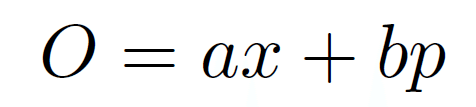
というのも、定数a,bのどちらかが零でなければ、Oの測定誤差には原理的な下限が存在するのではないかと考えていたからです。下記のようにOの測定誤差δOを考えると、それは位置の誤差δxと運動量の誤差δpを使って

と書けると考えられます。するとOの平均2乗誤差は次のように評価できて、プランク定数と非零のabの積で決まる下限値があるのではないかとウィグナーは疑念を持っていたのです。

もしこの予想が正しければOという量は決して正確に測定できないのですから、その意味では観測可能量ではないと考えられます。
しかし現代の量子測定理論を踏まえると、このウィグナーの誤差下限の議論には根拠がないことがわかります。実際には例えば「スクィージング」という技術を使うことで、Oも任意に小さな精度で測定可能であるからです。
まず円運動をする磁場中の電子を考えてみましょう。その電子の半分の周期だけ電子の状態を時間発展させた後の位置測定から、元の時刻での電子の運動量の確率分布がいくらでも正確に測定することは可能です。

このことについては下記教科書の第10章に書いています。
ここで半周期後ではない他の時刻において電子の位置を測れば、Oの確率分布を得ることができるのです。z方向にかけられた一様磁場中での電子の位置のx成分とy成分のハイゼンベルグ演算子は、下記のように解けます。

右辺に現れている演算子は時刻t=0での演算子、即ちシュレディンガー演算子です。時刻tを変えて左辺の位置座標を測定すれば、その結果からいろいろなaとbに対応する右辺の位置と運動量の足し合わせのOの情報が得られるのです。
これは磁場による電子へのスクィージングを使ったOの測定になりますが、光子の偏極でも光学素子を使ったスクィージング操作の実験を考えれば、この偏極自由度に対応するOは測定できることが知られています。
最初のウィグナーの議論がうまくいっていないのは、Oを測定するときに位置と運動量を別々に測定をして、その結果を足し算したからです。最初にスクィージング操作をしてから位置測定だけをすれば、原理的なOの測定誤差の下限は現れません。前世紀には観測できないと思われていた量も、現在ではいくらでも精密に測定できます。また何が観測可能な物理量であるかという問題についても、現代の量子測定理論は明確な答えを持っています。これについては下記記事も参照してください。
いいなと思ったら応援しよう!

