ソーキンのパラドックス：相対論と量子測定の整合性に関する誤解

現在では量子測定理論を通じて量子力学での観測過程は精度高く理解をされるようになりました。またいわゆる波動関数の収縮を発端として前世紀に散々論じられた「観測問題」も、量子力学には存在していなかったことが現在では下記記事のようにハッキリとしています。

波動関数は複数の物理量の確率分布をまとめて１つの数式で書いたものに過ぎません。確率分布に入っている量子情報こそが、波動関数の正体であるとも言えます。

一方で、相対論と量子力学を融合させた場の量子論における量子測定理論は、現在でも完全には完成をしていません。ただしこれは無限次元自由度を数学的に扱う技術的側面で完成を見ていないだけとも言えます。現時点で特に物理として問題となることは、相対論的な量子測定理論では起きてはいません。

前世紀の終わりには混乱があって、「ソーキンのパラドックス」というものが提案されたこともありました。これはソーキンさんが[1]の論文で提案をしたもので、量子場の理想測定を考えると、相対論的な因果律を壊すという内容でした。

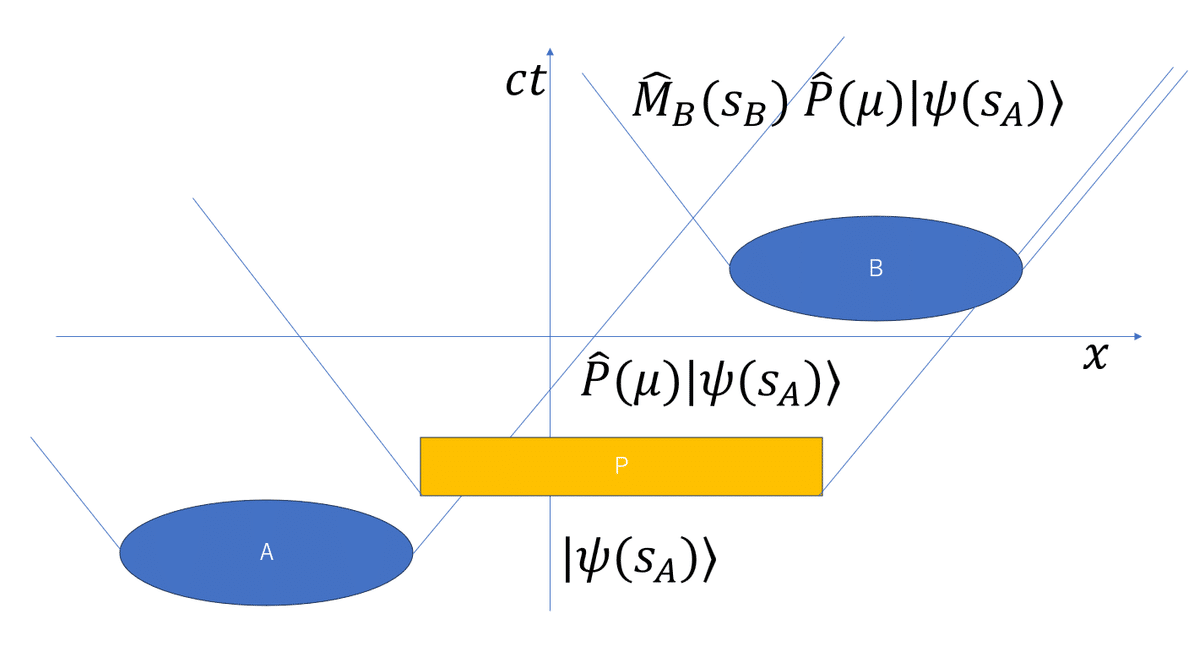
例えば図１のように平坦な1+1次元時空を考えます。その時空には２つの領域ＡとＢがあります。ＡとＢは相対論的には互いに「空間的」に配置されており、相対論的な因果律から物理的な効果をＡからＢへと伝えることはできません。しかし場の理想測定をすると、ＡからＢに情報を伝えられる可能性があると、ソーキンさんは指摘したのでした。

図１

まずこの時空内で相対論的な量子場を考えましょう。十分過去にはこの量子場は例えば真空状態であったとします。そして領域Ａにおいて、領域Ｂに伝えたい情報に応じて場を励起します。図１ではＢに送りたい情報をS_Aとしてあります。

次にソーキンさんは、図２のようにＡとＢの中間にある時空領域Ｐで場の理想測定を考えます。領域Ｐの左側の一部は領域Ａの未来の光円錐領域を含んでおり、Ｐの右側の一部は領域Ｂの過去の光円錐領域を含んでいます。そのＰでの理想測定の結果の出力をμと書きます。このμの値に応じて、測定後の場の状態は収縮をし、その各収縮状態は領域Ａで書きこまれた情報S_Aに依存するようになります。その収縮状態において、時空領域Ｂの物理量を測定をすれば、その確率分布はＡの情報に依存するというのです。この実験を何回も実行すれば、因果律的には繋がらないはずの領域Ａから領域Ｂへと情報を伝えることができます。これが「ソーキンのパラドックス」の概略です。

図２

これを以て、相対論的な場の量子論には「観測問題」があると主張をする科学哲学者も居ますが、実はパラドックスでも何でもありません。

まず重要な点として、場の量子論では厳密な意味での理想測定（射影測定）は存在をしません。そのような測定を実現しようとすると測定エネルギーが発散してしまいます。また相対論には剛体というものが存在しないため、領域Ｐのような有限サイズの時空領域で、Ｐ全体に及ぶ１つの結果を瞬間に読み出せる量子測定機は存在しません。Ｐの各部分領域に配置をした個々の測定機からデータを読み出し、それをある未来の時空点で集積をして解析を行って結果を出力するには、有限の時間がかかります。図３では、Ｐの各地点のデータは光速度以下で領域Ｃに集約をされて、出力μが作られています。

図３

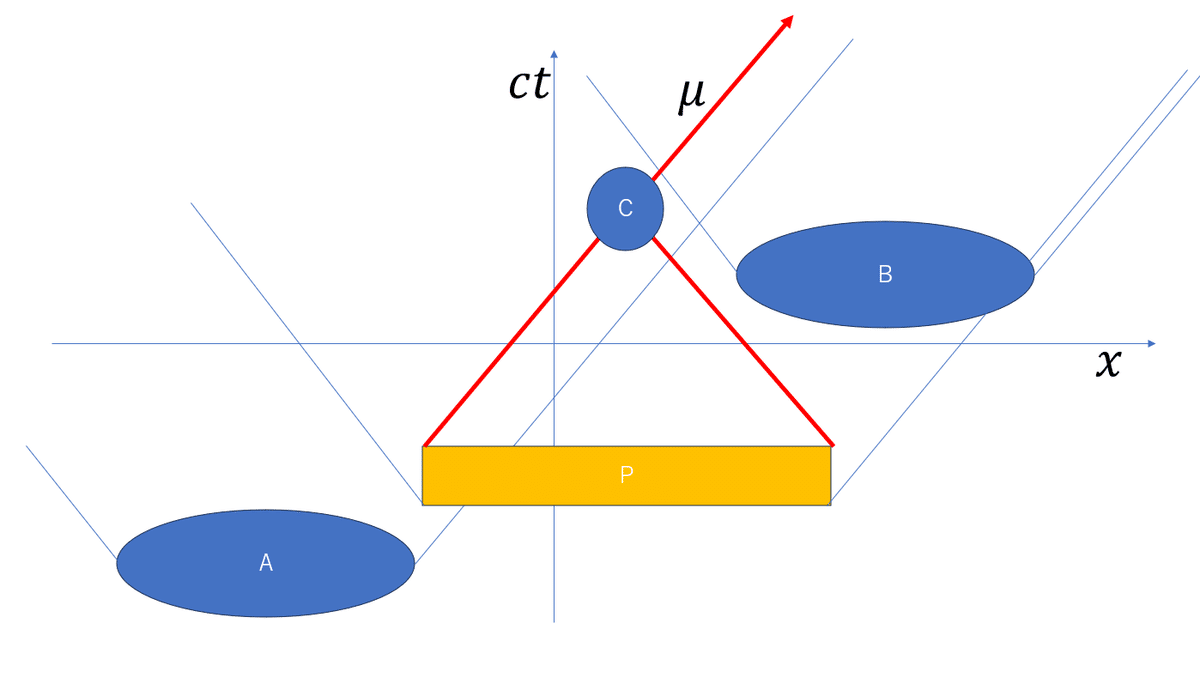
Ｃから送られるμがＢの観測者や実験装置に届くのは、Ｂより未来の時空領域になります。元の領域Ｂではμを決して知ることができないため、ソーキンさんが提示した量子場の状態収縮は領域Ｂでは起き得ません。従って領域Ａで量子場に書き込まれた情報を領域Ｂで読み取ることもできません。従って「ソーキンのパラドックス」は起きていないのです。

相対論的な因果律を破るような量子測定の実験や観測の報告は、現在全くありません。理論的にも、相対論のダイナミクスを厳密に満たす量子場や測定機ならば、それらが相対論的因果律を破る必然性は全くないのです。

[1] R.D. Sorkin, Impossible measurements on quantum fields, in Directions in general relativity: Proceedings of the 1993 International Symposium, Maryland, vol. 2, pp. 293–305, 1993.