
調和振動子モデルのユビキタス性
調和振動子は、物理学において重要なモデルを提供します。このモデルを最初に習うのは、多くの場合バネの力学系においてではないでしょうか。

図1のバネにつるされた物体は、平衡点x=0において安定化しています。多少バネを伸ばしたり縮めたりしても、その変位を戻そうとする復元力が働くために、このX=0の状態は安定を保ちます。そしてそのバネの力はバネ定数をkとしたフックの法則、F=-kXに従います。
拙書『入門現代の量子力学』の第9章でも量子調和振動子を取り上げています。
特にP145では、教育的にも重要な下記のようなコメントを加えました。
この量子的な調和振動子は、多くの複雑な量子系に弱い線形的刺激を与えた
ときの普遍的な振る舞いを記述する重要な系であるため、その応用も幅広い。
安定性を保つ状態にある様々な系の数理モデルの多くは、実はこの調和振動子で記述できるのです。バネの理解だけのために調和振動子モデルがあるわけではないのです。
まずは簡単のために、一般のポテンシャルV(x)の影響を受けて1次元空間の中を運動する質量mの粒子を考えてみましょう。その運動方程式は下記で与えられます。

ここでV(x)はバネの場合のポテンシャルに限定しません。この粒子はある点x=xoにいつまでも安定して居られる性質があると観察されたとしましょう。その点では粒子に働く力Fは零であるはずなので、V(x)は

を満たします。更にその点にある粒子に少しだけ変位を加えて力を測ってみます。物理学ではこのことは「系に微小摂動を加える」とも表現されます。世の中にある実際の粒子には、外の環境から様々な微小摂動が与えられてます。粒子のx=xoの状態が安定であるという意味には、このような微小摂動を粒子に加えても、その運動がx=xoから大きく外れていかない性質があることも含まれています。そしてこの性質を保つ多くの場合、V(x)が与える力はx=xo周辺においてフックの法則を満たす復元力となっているのです。特にx=xoでのV(x)の2階微分は、ある正の値を持ちます。

この性質から調和振動子モデルがx=xo周辺で導かれるのです。それを見てみましょう。まずポテンシャル関数V(x)をx=xo周辺で、下記のようにテーラー展開します。
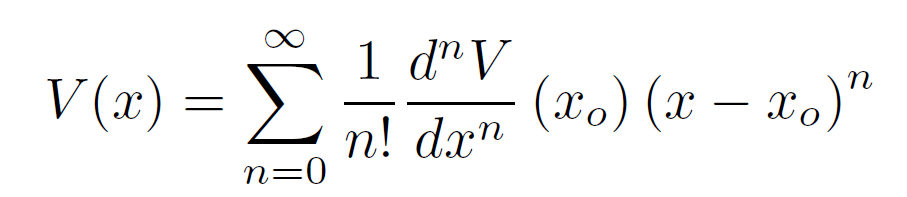
そして正の2階微分係数を正のパラメータωを使って下記のように置きます。

するとV(x)はx=xo周辺では以下のように近似されます。

テーラー展開の高次項は変位の微小性から無視できます。ここで粒子の位置座標を、以下のように平衡点での値+微小変位と分けてみます。

これと(2)式を(1)式の運動方程式に代入すると、

という近似の結果を得ます。これはまさしく調和振動子の方程式です。つまり一般的なポテンシャル関数V(x)でも、平衡点近傍では調和振動子モデルで記述をされるという普遍性が現れます。もちろんV(x)のテーラー展開の高次項は、変位δxを大きくしたり、長時間粒子の運動を追いかけたりすると、粒子の運動に影響を与えるようになります。しかし長時間ではなく、また変位が微小である限り、調和振動子のフックの法則の力に比べて非常に小さな効果しか生みません。
今は簡単のために1次元空間の1粒子の話に限定しましたが、3次元空間中の多粒子の場合でも、同じように調和振動子モデルが平衡点近傍に現れます。
多粒子の位置座標を全て並べて、その自由度の数をNとし、その各座標の肩には区別のための添え字aを加えます。このaは1からNまで動きます。このときの運動方程式は下記の式です。

このポテンシャルVは、N個の変数に依存する多変数関数です。今この運動方程式に従う系が、ある点で安定な平衡になっているとします。その点ではポテンシャルからの力は消えるので、下記の条件が成り立ちます。

これを満たす点での系の安定性から、位置座標に関するポテンシャル2階微分行列は任意のベクトルξに対して下記の正定値性を満たします。
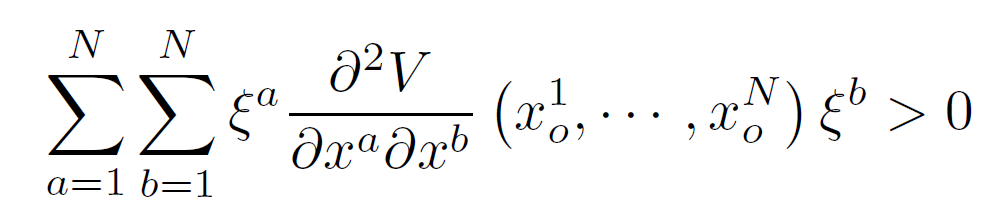
ここで再び各位置座標の自由度を「平衡点+微小変位」と分解します。

これを(4)式の運動方程式に代入すると、

という近似ができます。ポテンシャル2階微分行列が対称行列であることを思い出すと、それはある回転行列Rによって対角化できることがわかります。対角後の行列においては(5)式の2階微分行列の正定値性から、各対角成分は正であることが保証されています。

そして座標の変位を
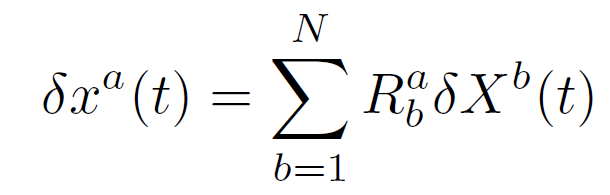
と書き直すと、(6)式の運動方程式は

というN個の独立な調和振動子の方程式に変形をされるのです。
今までは多粒子系で説明をしましたが、xという自由度は、安定性をもつ任意の系を特徴づける自由度に置き換えることも可能です。例えば巨大なビルや、新しく発見された物質の安定性を記述するのも、微小変位の範囲であれば、上と同じ解析が可能なのです。その意味で調和振動子という数理モデルはユビキタス性、つまり身の回りの多くの安定系において遍く現れる性質があるのです。仮に空から落ちてきた未知の隕石を解析する場合ですら、その表面を軽く叩いてその音のスペクトル解析をするときに、この調和振動子の数理モデルはスタート地点として有効であるという強みがあるのです。
拙書『入門現代の量子力学』第9章では、生成消滅演算子から作られる最も簡単で、かつ系の安定性を保証するハミルトニアンの構成によって、量子調和振動子モデルが導入されます。この背景には、上で述べた調和振動子のユビキタス性があるのです。調和振動子モデルで系の微小変位の運動が捉えられれば、次にその補正として生成消滅演算子から作られるより高次の項をハミルトニアンに加えて摂動的な解析を行うこともできます。その意味で調和振動子は理論解析の常に重要な出発点になっているのです。
いいなと思ったら応援しよう!

