
ハミルトニアンの定義域には入るのに、その2乗演算子の定義域には入らない関数
量子力学の関数解析に対する数学と物理学での価値観の差を、改めて書いておきます。
数学では、言わば1つ1つの自己共役演算子が主役で、それが作用する状態空間は脇役です。1つの演算子ごとにそれが作用する関数の定義域を決めています。ですから演算子毎にそれが定義される状態空間は異なっているとも言えます。実際には個別の演算子の各定義域を全部含むように、数学としては扱いやすいヒルベルト空間を考えています。ただしこのヒルベルト空間では、ある演算子の定義域には含まれるその元の関数が、他の演算子の定義域には含まれていないということも、頻繁にあります。
一方物理学では状態空間が主役で、それに自然に作用できる運動量や位置などの可観測量の作用素が脇役です。物理的に許容される波動関数の定義域を考えて、状態空間を最初に定義します。そしてその空間の元を同じ空間の他の元に写像するような演算子を求めて、その理論での可観測量の集合全体を決めるという順序で考えます。またその波動関数の時間発展も、この状態空間から飛び出さずに、その状態空間の中だけを運動するように、シュレディンガー方程式を定義します。
物理学で演算子ではなく、状態空間が「主役」なのは、そもそも量子力学が物理量の値の確率分布に基づいた普通の確率論であり、状態ベクトルや波動関数は、量子状態トモグラフィ法によって定義をされる、その確率分布の1つの表記に過ぎないからです。物理量に対応する演算子は、その状態空間としてのベクトル空間を導入してから、改めて定義をされます。
この数学と物理学の差を理解するために、x=0とx=aに壁がある1次元無限井戸型ポテンシャルの問題を、それぞれの立場で考えてみましょう。

数学の立場では、例えばハミルトニアンという1つの演算子を主役にして、それが自己共役になる定義域は何かと考えます。その条件は一般にはいろいろあるのですが、無限井戸問題の場合にはΨ(0)=Ψ(a)=0という境界条件によって定義域を定めています。この条件を加えたヒルベルト空間を、数学では状態空間としているのです。
しかし物理学の立場で言うと、Ψ(0)=Ψ(a)=0で指定されたその状態空間には不満足な点があるのです。単に壁の両側で波動関数が消えるという条件ならば、下記の2次関数もその条件を満たし、物理的な状態を表すはずです。しかし問題が起きます。まずハミルトニアンを2回作用させてみましょう。

すると2回作用された後の関数は恒等的に零となってしまいます。これは矛盾を生じさせます。ハミルトニアンを1回作用させた関数のノルムは下記のように非零です。素朴にハミルトニアンの自己共役性(の一部であるエルミート性)を使って、この結果と同じ非零の値であるはずのハミルトニアンの2乗の期待値を出そうとすると、それは上の計算から零となっており、合っておりません。

つまり普通の意味でのハミルトニアンのエルミート性が壊れているわけです。しかし数学では、この点は問題視されません。それはハミルトニアンに対する定義域と、そのハミルトニアンの2乗に対する定義域が異なって良いからです。この2乗演算子に関してはΨ(0)=Ψ(a)=0だけでなく、さらに以下の境界条件を付けた集合がその定義域になります。
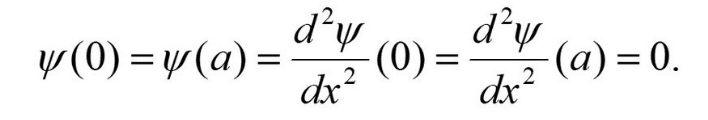
つまりハミルトニアンの2乗に対しては、ハミルトニアンの場合よりも小さな関数空間をその関数にとっての状態空間として考えていると、言っても良いです。数学者にとって、先の変な計算結果は、この関数がハミルトニアンの定義域には入っていても、ハミルトニアンの2乗の定義域には入っていなかったことを意味するだけです。
ところが物理学ではそうはいきません。ハミルトニアンを測定して1つの値を得たら、その2乗やハミルトニアンの任意の関数の値も、自動的に得られてしまっているからです。

その意味で、物理的な波動関数がハミルトニアンの定義域には入っていれば、その関数はハミルトニアンの2乗やハミルトニアンの任意関数の定義域にも入っていないと困ります。無限井戸問題の状態空間でも、古い初等的教科書にあるようなΨ(0)=Ψ(a)=0という条件だけ決まるというのでは、演算子の定義域がたびたび異なって、計算間違いを誘発します。それでは物理として不便極まりありません。
たとえば波動関数に作用するハミルトニアンのスペクトル分解を使って、そのハミルトニアンの任意関数の演算子そのものを下記のように定義するほうが、物理学を反映した数学として、まだ自然だと言えます。(証明をされるスペクトル分解の「定理」ではなく、演算子の「定義」だということに注意。)

上の関係をもう少し数学的に書けば、以下のようになります。
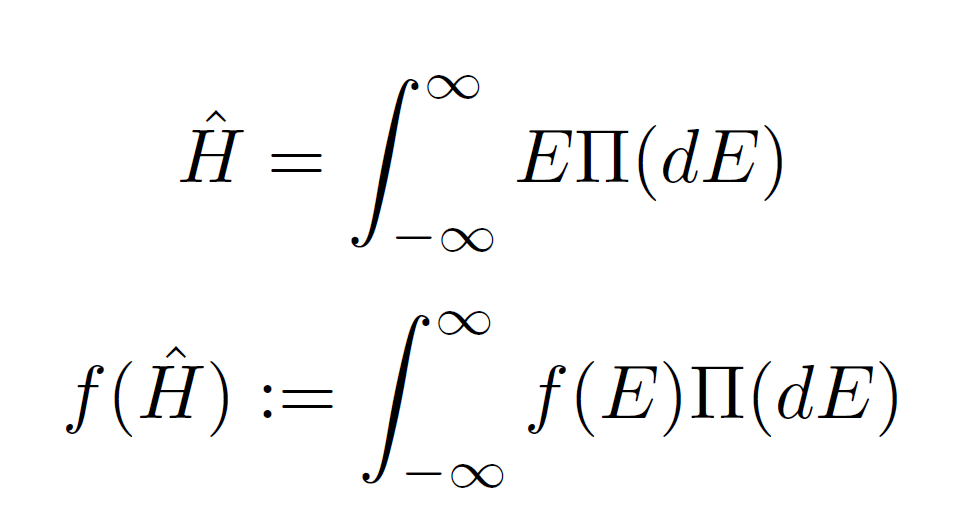
数学の関数解析での通常の扱いとは異なりますが、このように修正をすれば、確かにハミルトニアンの定義域とその任意関数の定義域は自動的に一致をします。
更に言えば、スペクトル分解で演算子を定義するよりも、簡単に下記の条件を波動関数に課すだけで、2階微分演算子のハミルトニアンを2乗したものを、そのまま4階微分演算子として扱っても計算間違いをしなくて済むのです。
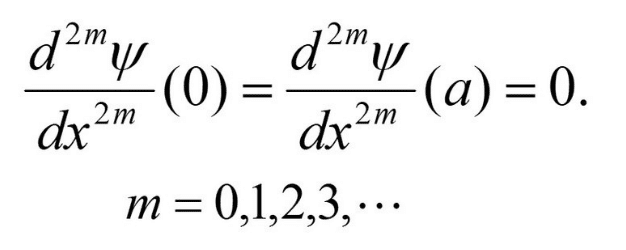
そしてこの条件を加えても、無限井戸問題のハミルトニアンの固有関数は古い教科書の結果と同じになります。ですから通常の答えも修正しなくて済むのです。その意味でこの条件を加えることは、理論にとって「経済的」とも言えます。

まとめると、ハミルトニアンの2乗の期待値の計算で問題を起こしていた先の2次関数は、2階微分が壁で消えないためにトラブルを起こしていたのです。その関数は、物理的な状態空間には属さず、そのため自然には許容されない関数であったということだけなのです。その解決法の1つが、ハミルトニアンの2乗やハミルトニアンの任意の関数の演算子を、(1)式のスペクトル分解の関係式で定義をしてしまう方法。もう1つは、スペクトル分解の定義を用いず、(2)式の条件を波動関数に課すこととなります。

いいなと思ったら応援しよう!

