どうして波動関数は連続で微分可能なのか？

学部の量子力学の講義では、波動関数は連続で微分可能と教わることが多いと思います。でもその理由をきちんと理解している人は少ないようですので、ちょっと書いておこうと思います。

実証科学としての物理学の立場ならば、実際の波動関数がプランク長（約10のマイナス35乗メートル）くらいのミクロ領域でも微分可能かどうかは、実験からはまだ検証されていないと、正確に答えます。

また理論的にも、位置座標が連続的であることには疑問があります。本当に連続ならば、それを実証する測定方法を提示しないといけません。仮に位置座標が連続変数だとして、どのようにプランク長以下の大きさの領域で粒子の位置を測定をするかを考えてみましょう。一般に極めて狭い空間領域に感度をもつ測定機を作るのならば、その位置の量子揺らぎΔxは極めて小さくする必要があります。不確定性関係からこれは非常に大きな運動量の量子揺らぎΔp、そしてそれがもたらす大きなエネルギー揺らぎΔＥを要求します。そのように大きなエネルギー揺らぎを狭い領域に注入しつつ、その領域の位置を測ろうとすると、ミニブラックホールがその場所にできてしまう可能性は大きくなります。せっかく点粒子の位置を測ろうとしたのに、測定装置が生み出すブラックホールがその位置を隠して測れなくしてしまいます。つまりプランク長以下の位置座標の測定は、概念的にも未解決なままの問題なのです。

デルタ関数型の１次元ポテンシャル問題を考えれば、波動関数の微分係数はその点で左右で異なり、微分可能ではありません。しかし実際の実験では、そういうポテンシャルは近似的にしか作れませんし、その現実の系では連続かつ1階微分も可能な波動関数で、その実験結果は説明できています。

微分不可能な波動関数が普通の実験で出てこない理由は、単純にその状態を作るときのエネルギーコストにあります。微分できない波動関数は、普通に考えると運動量エネルギーが大きくなってしまうので、そのエネルギーを前もって用意することが実験的には難しいというだけです。

例えばポテンシャル問題の束縛状態を求める場合ならば、その状態のエネルギー固有値は有限であるという条件も、物理として既に要求されているため、運動エネルギーが発散してしまうような微分不可能な波動関数は、最初から除外されているわけです。

量子力学を数学として捉えてしまう物理学徒が、何も物理を考えずに無限次元の連続的状態空間へ完備性を課してしまうのも問題です。完備性は、実証科学として実験から要求されている事実ではありません。数学として綺麗で、証明があれこれ簡単にできるモデルに過ぎません。たとえば量子重力の効果まで採り入れた場合に、自然がその連続的な完備モデル通りになっている保証はないのです。

調和振動子などの粒子系モデルを有限次元の状態空間を用いて定義しても、これまでの実験結果とは全て整合します。したがって完備性や連続性のない理論が実験で否定をされているわけではありません。

この教科書においても、第８章で粒子の位置演算子と運動量演算子を解説していますが、状態空間の次元Nを無限大に取らなくても、それらの演算子は定義できています。そしてNが十分に大きければ、第９章の調和振動子も、その有限次元行列で記述可能となり、これまでの全ての実験結果とも矛盾をしません。Nが有限でも調和振動子のハイゼンベルグ方程式もちゃんと満たします。ただし空間は離散化されます。しかし十分に大きなNに対して、その空間間隔は、量子重力が効きだすと考えられるプランク長よりも小さくできます。空間が離散的なままでも、プランク長領域まで実験が達していない現状の物理学の理論として、何も問題はありません。

具体的に考えてみます。Nが有限の状態空間で、下記のN本の基底ベクトルを考えてみましょう。

そしてこの基底で下記のようなN次元正方行列を定義します。これはこの基底ベクトルに対する消滅演算子（下降演算子）になっています。

そして生成演算子（上昇演算子）はエルミート共役で定義されます。

例えば各基底ベクトルは、最初のベクトルに生成演算子をどんどんかけて、適当な規格化をすれば得られます。

なお消滅演算子と生成演算子の交換関係は、有限次元だと少しずれていて、このままでは単位行列に比例はしていません。しかしそれでも飛び飛びの空間での調和振動子のモデルとかは作れてしまいます。

飛び飛びの空間での調和振動子モデルを作るには、下記のような数演算子を定義すればできます。

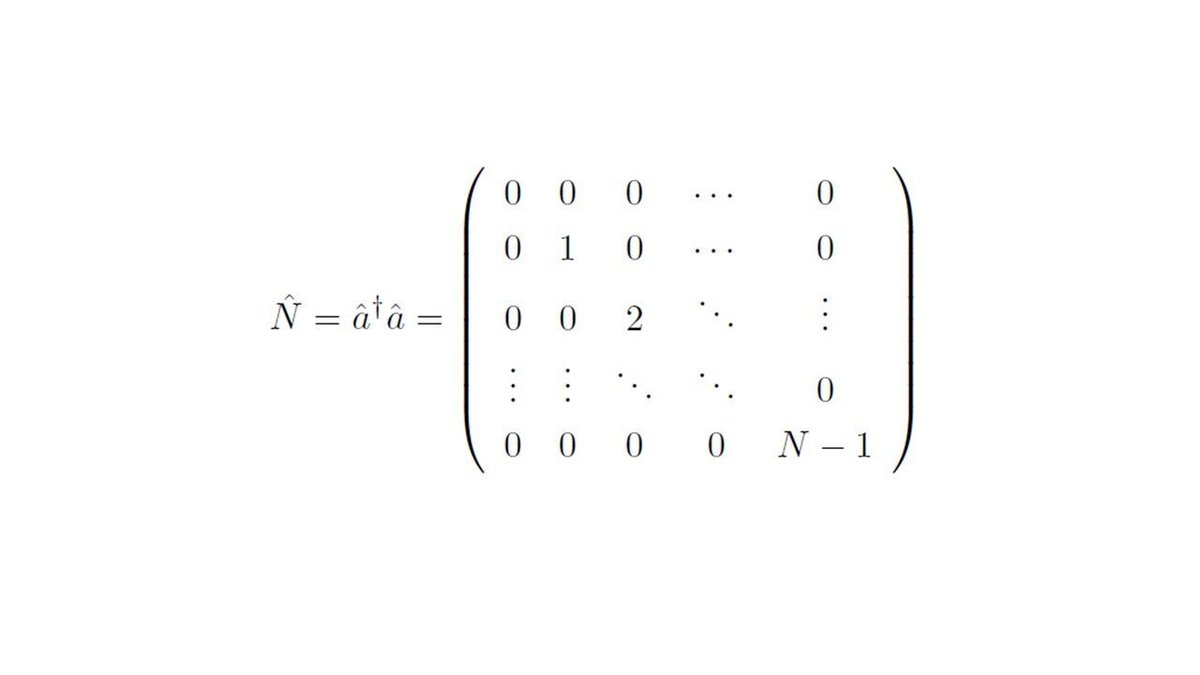
最初に考えた基底ベクトルは、この数演算子の固有ベクトルになっているのも簡単にチェックできますよね。

この有限次元の量子力学においても、長さの単位を持つ定数Lとプランク定数を導入すれば、下記のような（飛び飛びの空間の）位置演算子と運動量演算子を導入できます。

ただ連続空間の場合とは異なっていて、位置演算子と運動量演算子の交換関係は正確にはまだ単位演算子Iに比例はしていません。

Nが有限の場合の位置演算子の固有値と固有ベクトルを下記にように考えられます。運動量演算子の固有値と固有ベクトルでも、同様です。

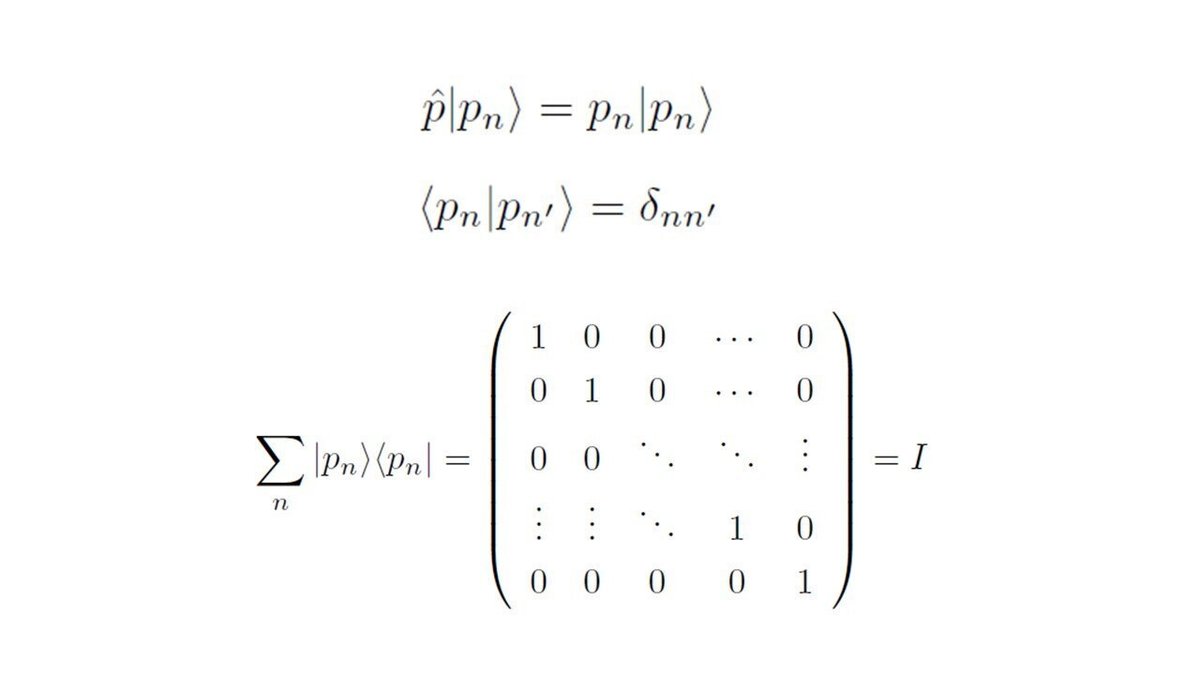
飛び飛び空間でも調和振動子モデルを作れる理由は、下記のように数演算子と生成演算子の交換関係が連続空間の時と同じになるからです。

ちなみに消滅演算子の交換関係も、連続空間の場合と同じです。

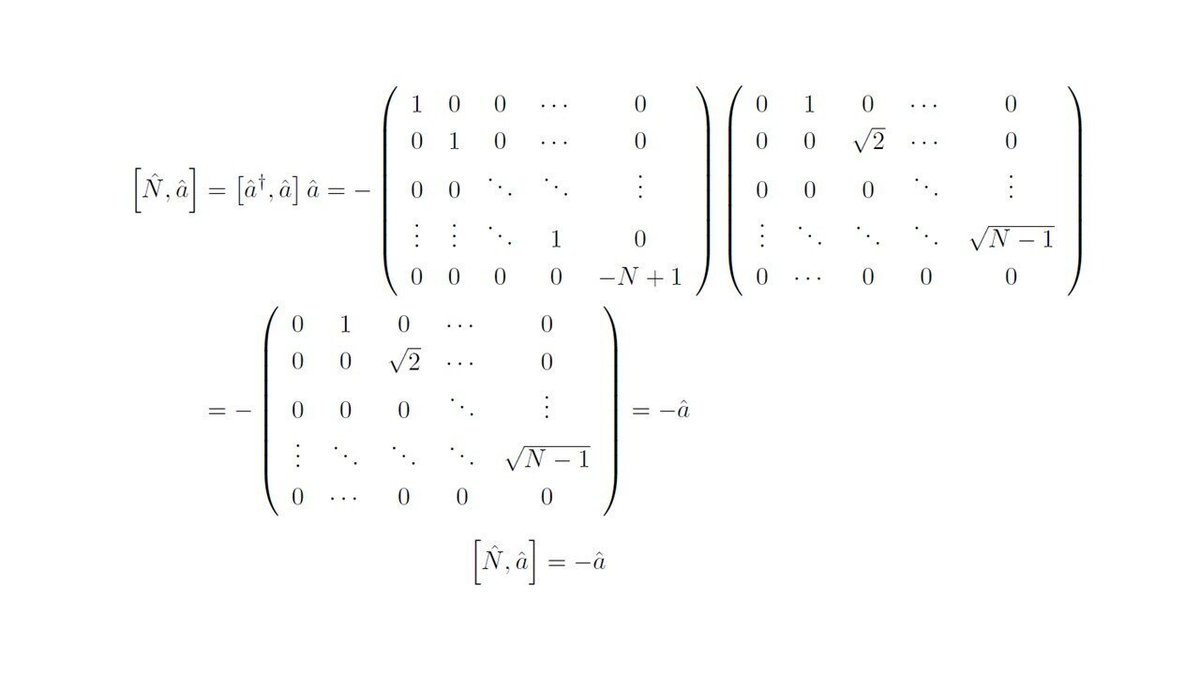
そこで角周波数の単位をもつωという定数と数演算子を使ってハミルトニアンを構成して、下記のユニタリー行列で時間発展を考えましょう。

この演算子を使って位置演算子と運動量演算子のハイゼンベルグ演算子を定義すれば、古典の調和振動子と同じ運動をすることが確認できるわけです。飛び飛び空間にも関わらずです。

ここで下記のように、この調和振動子の質量を導入します。

すると位置と運動量のハイゼンベルグ方程式の形は、ぴったり古典的な調和振動子の運動方程式の形と一致するわけです。

ですから位置と運動量の期待値も、古典的な運動方程式と同じ方程式を満たします。これはエーレンフェストの定理で出てくる古典的な調和振動子の方程式と同じです。

空間を連続にしたければ、ℏωNに比べて低エネルギーしか持たない量子状態だけを考えて、Nを無限大にとれば良いのです。これによって連続空間での量子的な調和振動子モデルが出現するわけです。

このような思考ルートでも、普通の連続空間での量子調和振動子の理論が構成できるので、厳密な数学に悩む題材は実際には物理学にはないのです。数学的に厳密な関数解析の知識がないと、調和振動子の量子力学さえ理解できないというわけでは決してありません。