無限に深い量子井戸に潜む、物理学徒の数学への隷属とその開放

量子力学を学ぶとき、数学の厳密な関数論の知識が不可欠、もしくはそれがないと理解できない例があると主張される教科書などがあります。それを読んだ物理学徒たちの中には、自分達が普段行っている計算は「いい加減」で「不正確」だと思ったり、また一知半解の数学徒からマウントをとられて劣等感を持ったりする人もいるようです。そしていつの間にかに「数学が上で、理論物理学は下」だと、数学の理論こそが正しい物理学の理論を与えるものだと、潜在意識でまで思うようになり、数学に隷属化される物理学徒も見受けます。しかし理論物理学者である私は、それは全く的外れだと考えています。

フォンノイマンは関数論を使って量子力学の数学的基礎を開拓したことでも有名です。彼は天下り的に量子状態の空間は完備性をもつヒルベルト空間であると定義をしました。そして物理量はその空間に作用をする自己共役演算子であると、また定義をしました。ここで「定義」をしたという点に注目をしてください。それに関して証明や実証をしたわけではないのです。現在まで多くの量子力学に関する実験や観測が行われてきましたが、それらの結果のどこにも状態空間の完備性を要求する事実はないのです。ここで完備性とは、量子状態のコーシー列を考えたときに、その収束先も量子状態であるという仮定です。そうなのです。物理学としては飽くまで仮定なのです。つまり数多ある提案やモデルの１つに過ぎません。また実際の実験には誤差が必ず伴います。するとこれまでのそのような誤差のある実験データを全て説明さえできれば、フォンノイマンの理論ではない他の理論も物理学として十分に生き残っているものと位置づけられるのです。それこそが実証科学の考え方なのです。点粒子の量子力学においても、２乗可積分空間としてのヒルベルト空間を状態空間とすることは、まだ実験的に十分に検証をされていません。特にその空間の任意の元が物理的に実現をするかも確かめられていないのです。たとえば不連続で微分不可能な波動関数は、その状態を作るエネルギーコストが無限大に発散するため、物理的には無意味だと考えられます。また一方で、連続性すら持たない離散モデルでも生き残っているものもあります。例えば量子力学の調和振動子ですら、有限次元の状態空間と離散的な位置座標をもつモデルで十分に現時点の実験全てを説明してしまいます。数学的な関数論はそこには必要ありません。これについては下記記事をご参照ください。

そもそも物理学の営みは、数学とは全く異なります。物理理論に出てくる関数の定義域や値域さえ、本来は実験や観測を通じて実証的に詰めていく対象なのです。これについては下記記事をご覧ください。

結局物理学に出てくる関数は全て連続的であるべきかどうかさえ、実証科学としては確定をしていないのです。

今回は多くの教科書に出てくる無限井戸を考察し、数学の関数論を知らなくても、その物理は正確に扱えることを論じてみましょう。「無限井戸」とは、１次元空間のある有限の領域の外に無限大の高さのポテンシャルが存在し、そしてその領域の内側にはポテンシャルがない場合の問題のことです。ここではその内側領域を[0,a]とします。よく教科書にあるのは、そのポテンシャル壁の境界で波動関数が零になる固定端条件（Diricklet境界条件）を置く問題とされます。ここで波動関数の規格化条件は、その有限領域での波動関数の絶対値の２乗の積分が1になることを指します。

この問題で数学の関数論は重要だと指摘する人が挙げる例は、次の現象です。まず波動関数の時間発展を与えるシュレディンガー方程式から出発します。

特に領域内部ではポテンシャルは零なので、そのハミルトニアンの具体形は次のように運動エネルギー演算子で与えられるでしょう。

従って無限井戸問題で解くべき方程式は、以下の偏微分方程式となります。

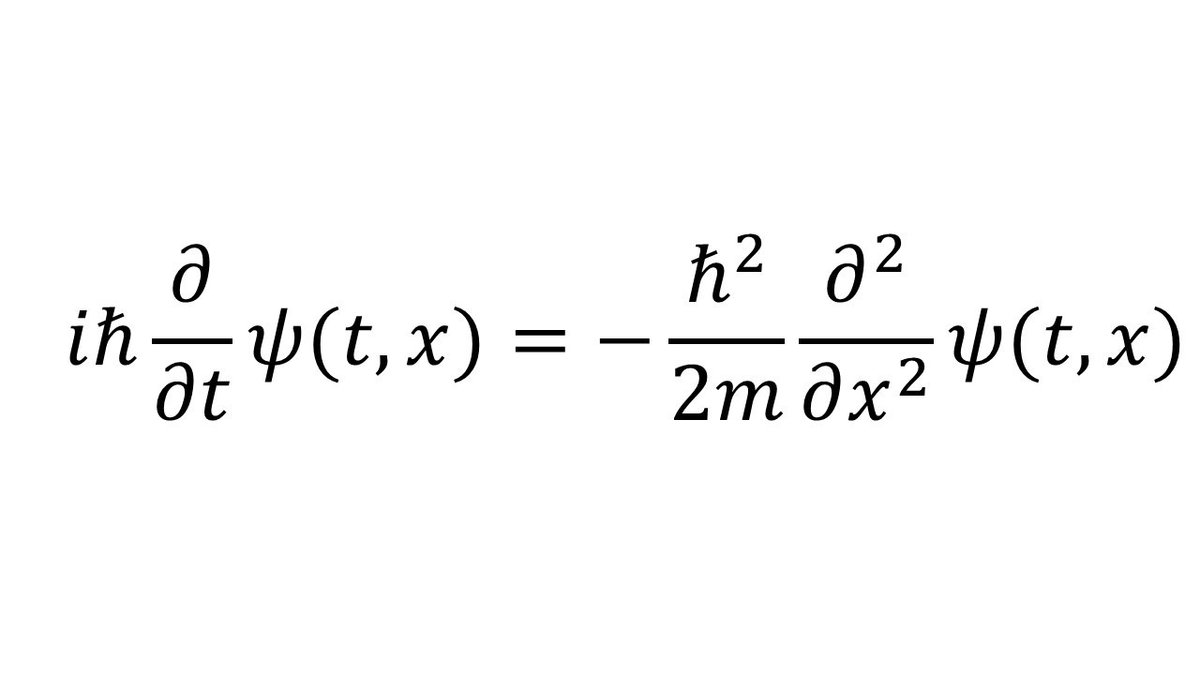
ここで壁での境界条件を満たし、規格化条件も満たす次の初期関数を時刻t=0に与えます。

するとこの初期条件を満たす解析解が次のように与えられます。

この時刻tの関数形を元のシュレディンガー方程式に代入すれば、それが解であることも確かめられますし、またt=0とすると元の初期関数が再現されています。しかし問題があります。時刻t>0で規格化条件を破っているのです。

時間とともに全確率は増加し、1より大きくなっています。これでは確率解釈が可能な解とは言えません。さらに時刻t>0で壁での固定端条件も破れています。「このような変な解が出てきたのは、数学の関数論を知らずに、シュレディンガー方程式を解いたからだ。だから物理学徒には少なくとも関数論の知識は必須である」という主張も、この例から成されることがあります。

それで脅迫されたように数学の関数論の教科書を急に開いて、非常な遠回りをしてしまう物理学徒も例年現れます。しかしそんな厳密な関数論を持ち出さなくても、実はこの問題は簡単に解決をするのです。まずこういう「異常」に出くわしたとき、物理学徒は自分の使っているツールをよく考え直してみるべきなのです。

まずハミルトニアンとは状態空間に作用をする演算子であるべきですが、これは本当に「演算子」であるかどうかに注目をします。状態空間を閉じさせる演算子であるのならば、今考えている状態空間の元全てを再び状態空間の元に移すはずです。しかし先ほどの初期関数に対してハミルトニアンはこの条件すら満たしていないのです。実際このハミルトニアンをこの関数に作用させると、下記のように非零の定数関数となります。

したがって壁の境界で零になるという条件を満たしていません。つまり考えている状態空間の外に、その元を飛ばしてしまうのです。これではそもそも良い演算子とは言えません。

境界条件を破る演算子では、時間と空間を離散化してシュレディンガー方程式を数値計算で解く場合にも、そもそもうまくいくはずがないのです。数値計算では本質的に

という関係を用いて、逐次的にハミルトニアンを初期波動関数にかけて、時刻tでの波動関数を求めます。そのn=1の場合の項が既に壁での境界条件を破っているのですから、有限時刻での波動関数もその境界条件を満たすわけがないのです。

また物理学として考えるとき、問題の設定の物理的妥当性を検証することも大事です。たとえば明らかなように、この世界には理想的な無限井戸などは存在しません。十分に高いポテンシャルを持つ有限井戸型ポテンシャルは実験で近似的に作ることはできますが、その高さを無限大することは決してできません。その物理として達成できない奇妙な極限を考えたことが、変な解を出す原因ではないかと目星を立てる能力も大切なのです。

そこで自然な系として有限井戸ポテンシャルを考えて、先の初期関数を考察してみましょう。有限井戸では井戸底の外側領域もちゃんとあります。波動関数はマイナス無限大からプラス無限大までの実数直線上で規格化される複素関数になります。先の関数は井戸の外の領域で厳密に零になっていました。つまりヘビサイドの階段関数を使って、以下のような形の関数を扱っていたことになります。

そして運動エネルギー演算子をこの関数に作用をすると、先ほど見落としていたデルタ関数に比例する下記の寄与が見つかります。

無限井戸でも本来はこのデルタ関数を与えるヘビサイドの階段関数の寄与を採り入れて問題を解くべきだったのでした。しかし実際の有限井戸の実験でエネルギーの量子揺らぎが発散するこのような初期状態を作ることはできないので、これも無限大ポテンシャル近似による間違いだと簡単に理解しても良いです。有限井戸にして、初期状態も実際の実験を反映するように滑らかな波動関数をとれば、普通にシュレディンガー方程式の初期値問題は数値的に解けます。

重要なのは、物理学徒が数学の関数論を知らなくても、物理自体に集中をして考察を深めれば、これらの問題点は気づける点です。それでは物理学徒はどのように無限井戸問題を解くべきなのでしょう。次にそれを考えています。

まず壁での境界条件をきちんと満たさせるために、波動関数と状態空間をきちんと制御しましょう。井戸内部のエネルギー固有値方程式の解のうち、壁で消える固有関数を考えます。でもそれだけでは足りません。固有関数にハミルトニアン演算子が何回作用しても、できる関数も同じ固定端条件を満たすようにしなければなりません。そうでなければハミルトニアンは状態空間で閉じる演算子にすらなりません。このことから物理学徒は次の無限連立方程式を解くことになります。

この解は良く知られているもので、エネルギー固有値とそれに対応する規格化された固有関数は以下で与えられています。

更にこの固有関数に関する次の完全性も証明されます。

この証明にも特に関数論の深い知識は必要ありません。フーリエ変換とデルタ関数の性質を知っているだけで十分です。まず円周の長さが井戸の内部領域の２倍の大きさをもつ以下のリングを考えます。

図１

このリング上で、図１のような奇関数となる複素関数を考えます。この関数は、井戸の内部領域に当たる部分での壁の固定端条件を満たすことが分かります。そして次の関係式が以下の方法で証明できます。

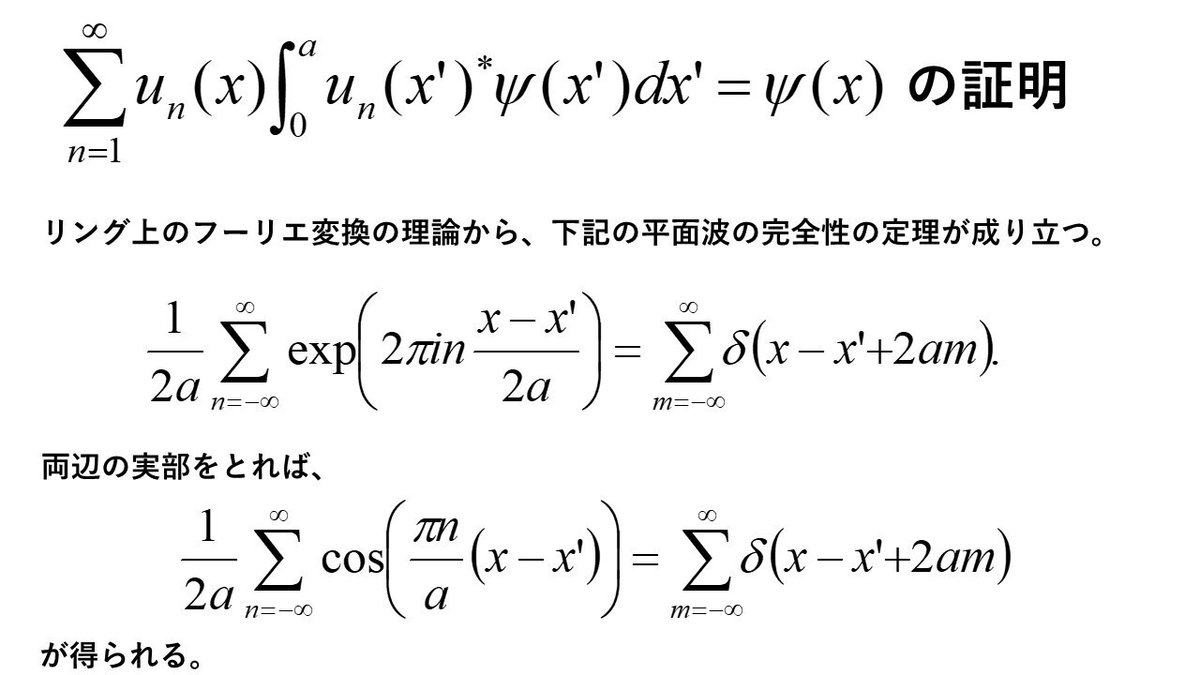
固有関数の重ね合わせで状態空間に属する波動関数を構成するのですが、無限和をとると壁での固定端条件が破れてしまう可能性があります。それを避けるには、下記のように有限だけどいくらでも大きくできる正整数Λを使って重ね合わせを定義すれば、全く問題はありません。また時間発展した後でも固定端条件は満たされます。

このような形の関数の集合で定義される空間を状態空間と定義すれば、壁での固定端条件は任意の元で成り立ちます。

さらにハミルトニアン演算子は必ず任意の元をこの空間の元に写像することも保証されます。またハミルトニアン演算子の２次や高次の積演算子も、任意の元をこの空間の元に写像することが保証をされます。またハミルトニアン、つまりエネルギーの確率分布の期待値や分散や高次モーメントの全ても必ず有限になります。そのような量子状態を実験で作ることは、エネルギーコストの観点からも問題はなくなります。

ただし注意が必要なのは波動関数ψ(x)にxを掛けるという演算は、このカットオフ理論には含まれません。つまり位置演算子は単純にxを掛ける演算子にはならないのです。xを掛けることで定義される演算子はその固有状態がデルタ関数となるため、その測定には無限大のエネルギーが必要なので物理としては実現をしません。代わりにΛ＋１次元エルミート行列の中で、Λ無限極限において「xを掛ける」に漸近する操作の１つを測定可能な位置演算子とする必要があります。そうすれば、厳密に空間１点の局在はせずに、多少の幅をもつ固有関数が許されて、エネルギーも有限になります。

また２乗可積分性で定義をされるフォンノイマン流のヒルベルト空間の状態も、任意の精度でこの状態空間の元で近似をできることが保証をされています。ヒルベルト空間とは異なり、この状態空間には完備性はないのですが、必ず生成には誤差を伴う物理的量子状態ならば、任意に小さくできるこの誤差は問題になりません。

それでは最初の初期関数の問題に戻りましょう。この関数もヒルベルト空間には属するので、任意の精度で今の状態空間の元で近似可能です。その近似系は次の形で与えられます。

ですから、その時間発展は以下のように書けます。

ここで和を一応無限和にしています。しかし実際の数値計算や現実の実験では、有限個数の固有関数の和にします。和の無限大を有限のカットオフΛに置き換えて、上で作った状態空間の元として扱えば、何も問題は起きないのです。

それから関数論は大事だと言う人でもやり勝ちな失敗は、無限井戸問題での運動量の扱いです。

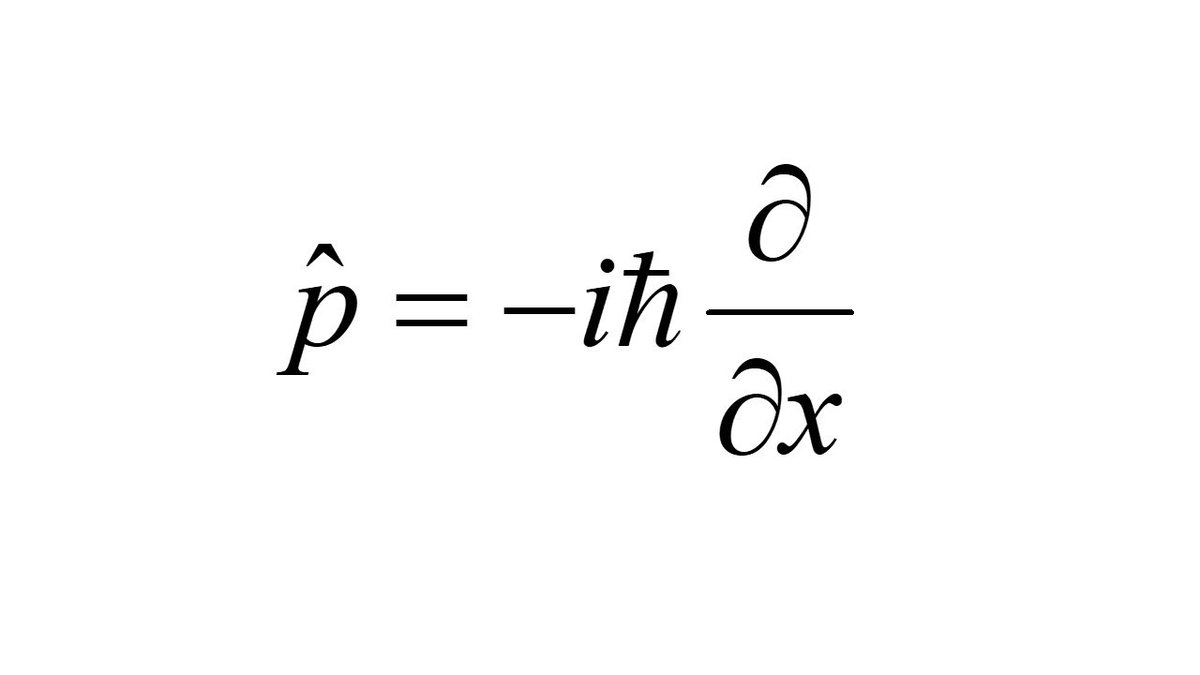
この演算子は無限井戸問題では、関数論での自己共役演算子にはなっていません。つまり本来は物理量ではないのです。もし自己共役演算子であれば、それを使って下記のように作るユニタリ演算子が存在して、無限井戸の波動関数を次のように変換をするはずです。運動量演算子は空間推進の生成子なのですから。

ところが、この関係が成り立ってしまうと、壁での固定端条件が破れてしまいます。これは運動量演算子が自己共役ではないことを意味しています。それどころか、今考えている固定端条件を満たす関数の空間での演算子にすらなっていません。つまり固定端条件を満たす波動関数にこれを作用させて作られる関数は、固定端条件を満たさないのです。つまり状態空間の外に元を飛ばしてしまう操作だったわけです。

関数論の扱いが重要だと主張しつつ、運動量演算子の期待値や量子揺らぎ、そして位置と運動量の不確定性関係を無限井戸で論じている教科書もあります。しかし物理量ではないとその教科書でも主張をされた「運動量」を測定して、期待値や分散を評価するという議論では、物理学徒は非常に混乱するだけなのではないかと思われます。

中途半端に数学の関数論を操るよりも、物理の本質に集中をして、何が物理的におかしいのか、それをどのように修正をすれば物理学として正しい答えに至るのかを、真剣に考え抜く物理学徒のほうが、結局は本質を深く理解できるようになると私は考えております。

また物理理論の厳密な数学化は物理学者の仕事ではないと、私は思っています。物理学者を例えるならば、下記記事にも書いたように「探偵」なのです。

自分達は「探偵」であることをしっかりと物理学徒は肝に銘じて欲しいなぁと私は願っています。