数学の演繹と物理学の演繹：２準位量子系を使って、３準位系の量子力学を実証的に演繹する
「演繹」という言葉があります。精選版日本国語大辞典（小学館）によると
１ 一つの事柄から他の事柄へ押しひろめて述べること。「身近な事象からすべてを演繹する」
２ 与えられた命題から、論理的形式に頼って推論を重ね、結論を導き出すこと。一般的な理論によって、特殊なものを推論し、説明すること。
とされている言葉です。数学における「演繹」ならば、基本的にはこの２番目の説明となるでしょう。しかし実証科学の物理学における「演繹」ならば、与えられた命題の妥当性も検討しなくてはなりません。実験観測を通じて検証できる命題でなければ、空理空論になってしまうためです。その意味では１番目の説明に出てくる例の中の「身近な事象」を実験や観測の結果とみなすことができるでしょう。その確かめられた事実や少なくと実証可能な要請を作業仮説として命題化し、「一つの事柄から他の事柄へ押しひろめて述べる」のが物理学とも言えます。
下記の教科書では、その実証科学的な精神に基づいて、情報理論の観点からの最小限の実験事実に基づいた論理展開で、確率解釈のボルン則や量子的重ね合わせ状態の存在などを証明することを論じています。「最小限の実験事実」がポイントであり、たとえば宇宙全体を調べ尽くさないと、眼の前にある物理系が量子力学に従うのかどうかを確かめられないのでは、意味がありません。
この教科書の第３章では第２章の二準位量子系の定式化を踏まえて、三準位系を含む多準位系の定式化を説明しています。下記はその引用です。
ここでは、たとえ未知のN準位系（それを物理系Ｘとしましょう）でも、任意のユニタリー行列に対応する物理的な操作が実現可能だと仮定しています。これは要請や命題と言えるものです。物理学者ならば、その謎のＸを手にしたときに、それが本当に量子系なのか、それとも他の自然法則に従う物体なのかを決める方法論を持つべきです。ユニタリー行列には必ず物理操作が対応するということを実際に確かめる手順を与えられれば、これを要請として出てくる結果を導くことは、演繹になります。基本的には第２章の二準位系の定式化と同じことを行えば良いのですが、ページ数の関係でそれは省略され、短く単に仮定としています。
ところがこの部分に関して玉川大学の中平健治さんという方が、下記の批判をアマゾンレビューに上げられました。
「著者が用いている前提（「前提のまとめ」以外に用いられているものも含む）は，複雑ですべてを明瞭な形で書き下すことが困難である上に，複素ヒルベルト空間を前提とすることと大差ないようなものになっています。大ざっぱに述べると，次の2点が即座に導かれるような前提を採用しています：(1)N準位系のある純粋状態が[1,0,…,0]というN次元列ベクトルで表される，(2)N次ユニタリ行列を施すという可逆物理操作が存在する。ここから，任意のN次元複素ベクトルに対応するN準位系の純粋状態が存在する（つまり複素ヒルベルトが現れる）ことがすぐにわかります。このため，そもそもなぜ複素ヒルベルト空間が現れるのかという多くの初学者が抱くと思われる疑問には答えていません。」（中平健治、アマゾンカスタマーレビューより）
同様の内容を下記のブログでも書かれています。
この批判に対して、中平さんと長時間の議論をさせて頂き、またその中で得られたものあって、それに関しては感謝しております。私からの対応は下記で見られます。
私は可能な限り望まれている形式での回答提示を目指しましたが、ほぼ最終回答となる時点で中平さんは無視をし、しかも真摯に議論をした私に対して、先のブログの中で『「演繹的に導けている」という主張を貫かれているようですが，このような行為は科学者・教育者としてふさわしくないのではないかと思います』と、2022年から現在までこのブログの該当部分を取り消すこともなく、誹謗中傷を続けています。（これについては現在法的処置も検討中です。）
私の立場としましては、中平さんが無視をしている、私からの最終的な回答で十分に事足りているという認識です。この内容をこちらのnote記事で少しまとめ直してみたいと思います。
まず私の教科書のスタンスですが、量子力学の導出について第３章と第１５章で分けて説明をしております。第１５章では相対論のように自然原理だけから量子力学を導く未解決問題のヒントを書きました。これからの若い世代の方々に是非挑戦をして頂きたい問題の１つです。また第３章では、二準位系の物理的操作を使って、多準位系のユニタリー行列が物理操作に対応するという実証実験に即した要請をし、それに基づいて確率解釈のボルン則や量子状態の線形重ね合わせを導いています。
例えば量子コンピュータでは、有限個の量子論理ゲートの組み合わせで、いくらでも小さな誤差で任意のユニタリー行列に対応する物理操作が可能です。ですので、未知の物体Ｘがもし量子系であれば、そのＸもユニタリー行列に対応する物理操作があると要請することは、現時点ではとても自然なことです。では、その要請自体は実験でどのような手順で確認をすれば良いのでしょうか？それを以下で説明します。そして確率解釈のボルン則と量子力学の状態線形重ね合わせを導出してみます。以下では簡単のために三準位系を例にしますが、定式化自体はＮ準位系にそのまま適応できます。
３つの状態をもつ物体Ｘが量子力学の法則に従って、ボルン則や状態重ね合わせを持つかを調べる最初のステップは、基準測定の構築です。実験家はこの測定をＸに対して見つける必要があります。この測定装置にＸを通すと、Ｘは３つの状態のどれか１つに分類をされます。その状態を１，２，３と名前を付けます。各状態に出てくるその頻度確率を、この装置では計測できます。
ここで基本測定が満たすべき性質は、反復可能性です。一旦装置から状態１に出てきたXを再び同じ装置に通した場合、必ず状態１で出てくるという要請です。
同様のことは状態２と状態３でも要請されます。
実験者がこの基準測定装置の製作に成功をした場合、今度は３つの状態から任意に選ぶ２つの状態から作られる二準位系を調べます。第２章で論じているように、任意の二準位系ではユニタリー行列に物理操作が対応をしています。このことを実験家はXに対して確認する必要があります。
例えばXの入射状態を調整して、出力状態が状態１と状態２だけからなる条件を見つけてきます。
これが分かったら、今度は二準位系での各ユニタリー行列に対応をする物理操作を同定し、そのリストを作ります。下図では最初の装置から出てきた二準位状態のXに物理操作を行って、再度測定装置に入れた後に、ちゃんと二準位系のユニタリー操作が実装されているかを調べています。状態３がこの物理操作で出てこないチェックをすることも含まれます。
実際の物理系ならば、例えば適当な外場を加えて、対応するエネルギー準位の間隔を不均一にし、下記のように状態１と状態２のエネルギー差に対応する振動数のレーザーなどを当てたりすることで、この物理操作が実現することも多いです。Xに対してもこのようなイメージで、状態１と状態２の制御を実現させるのが、このステップです。
これが済んだら、任意の二準位ユニタリー操作のリストが手元にあるはずです。そして各操作には二準位系でのユニタリー行列を下記のように３次元化して、紐づけをしておきましょう。
同じことを今度は状態２と状態３に対して行います。まずこの２つの状態で二準位系状態を作る設定を確立します。
その後で、任意の２次元ユニタリー操作のリストを作成します。
そして各操作に、また３次元に拡張された下記のユニタリー行列を紐づけします。
ここまでくるとXに対してかなりのことが分かってきています。次に状態２と状態３の間の操作の後に、状態１と状態２の間の操作を行います。
この合成された操作にも、下記の３次元のユニタリー行列を紐づけます。
この行列は２つのユニタリー行列の積ですが、各々の行列は下記の形になっています、そしてどのような物理操作と対応づいているかを実験家はもう知っています。
ここで重要なのは、任意の３次元ユニタリー行列は、この２つの二準位ユニタリー行列の積で書かれることです。（ただし物理的な意味を持たない全体の因子はここでは無視をしています。）
つまり二準位系の知見を踏まえることで、我々は任意の３次元ユニタリー行列に対応する物理操作のリストを手に入れられるのです。今後は合成された１つの操作に、この積を計算した後の３次元ユニタリー行列が紐づけられているとしましょう。
なお未知の三準位系Xの各二準位が量子系であるかどうかを調べる過程で、Xが量子系でないことが判明することもあり得ます。例えば教科書第１３章に出てくるポペスク＝ローリッヒ箱（PR箱）理論のような一般理論では、どれかの状態ペアについて、その２準位状態ベクトルをくるくると自由に回せる物理操作が存在できません。多準位のどの２つの状態からも量子ビット系が作れるというのが量子力学の特徴ですが、これが破れていた時点でＸは量子力学ではない法則に支配された対象であることが判明します。
これまでやってきたことは、単に操作をユニタリー行列の記法で書くことです。そうです。行列は単に利便性を狙って導入した記法の１つに過ぎません。実際に実験で出てくるのは、３つの状態に観測される確率分布だけです。それを勝手に人間が行列と紐づけた表示を発明しているだけの話です。なぜ量子力学に行列やベクトルの線形代数が出てくるかは、結局アフィン性などの確率分布の基礎的な属性のために過ぎません。
記法には人間が選択する自由がありますから、せっかくならば利便性が高い記法や表示を選択しましょう。まずユニタリー行列の生成子となる３次元エルミート行列には、トレースが零となるゲルマン行列という８個の基底行列が知られています。これは、二準位系のときの３個のパウリ行列の拡張です。この数学的な性質も広く使われている汎用性の高い道具です。その具体形を下記のように与えます。
ここで覚えておいて欲しいことは、最初と２番目の行列が対角化されている名前の付け方になっている点です。この選び方は後でとても有用になります。
ゲルマン行列はどれもエルミート行列ですから、それぞれユニタリー行列での対角化が可能です。固有値が並んだ対角行列と対角化に使ったユニタリー行列で、下記のように書きます。
ここに出てくるユニタリー行列も、２つの二準位ユニタリー行列の積で表わされ、そして対応する物理操作も今は実験家は知っています。すると各ゲルマン行列に対応する物理量の値の確率分布を実験で測定することがXの任意の入力状態に対して行えます。
まずゲルマン行列を対角化したユニタリー行列に対応する物理操作をXに対して行います。それで変換された状態のXを基準測定装置に通します。状態１に出てきた場合は、状態１の固有値が観測されたと定義します。ここで重要なのは定義をしたという点です。物理量はこの測定によって定義をされる概念なのです。
同様に状態２と状態３にもそれぞれの固有値を観測値として割り振ります。後は各状態の確率分布を実験で測るだけで、このゲルマン行列の物理量の期待値が求まります。
さてＸが量子系かどうかを確かめたい実験者にとって、いよいよ大詰めです。その手元には３次元ユニタリー行列がどのような物理操作に対応するかが書かれているリストがあります。それを駆使しながら、合計１０個の物理量の期待値を実験で測ります。任意の同じ状態のＸに対して、８個のゲルマン行列の物理量を測定します。そして同じ状態にあるＸに、連続的に変える３次元ユニタリー操作を施します。その操作の後でゲルマン行列の最初の２つだけ測り、その期待値のデータをとります。Ｘが量子力学に従う対象であれば、得られた１０個の期待値のデータには、特殊な２本の関係式が成り立つのです。またこの関係が壊れていれば、間違いなくＸは量子系ではないと言えます。
その関係式は以下の２本です。左辺は選んだユニタリー操作をした後の最初と２番目のゲルマン行列物理量の期待値です。右辺はなにも操作をしないまま測定をした、８個のゲルマン行列物理量期待値の線形和になっています。
その係数は、実は選んだユニタリー行列に対して、SU(3)群が満たす下記の式から一意に定められています。
この係数は具体的にはユニタリー行列に対して次のように与えられています。
この式から、この係数が実数であることも以下のように分かります。
この１０個の期待値の間の２本の関係式は、教科書第２章（2.6）式の二準位スピンにおけるスピン期待値のベクトル性の３次元版の拡張に過ぎません。この２本の関係式が実験で成り立つのならば、以下で示されるように、Ｘは確率解釈のボルン則や量子力学の状態重ね合わせを満たします。そこで実験家は理論家にデータを渡して計算をしてもらい、２つの関係式が実験で成り立っていたのかどうかを調べてもらえば良いのです。
その結果、確かに２本の関係式が成り立っていたとしましょう。すると以下の計算から、確かにボルン則が出てきます。つまり実験結果からボルン則が演繹されるのです。
まずゲルマン行列の始めの２つに注目します。既に対角化されているため、余計なユニタリー行列は要りません。
この２つの物理量の期待値は下記のように計算されます。
そして全確率が１であるという下記の条件式と合わせることで各確率は期待値から計算できます。
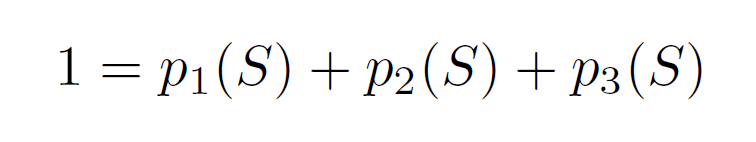
結果は下のようになります。簡単ですので、確かめてみてください。
３本の結果をまとめると
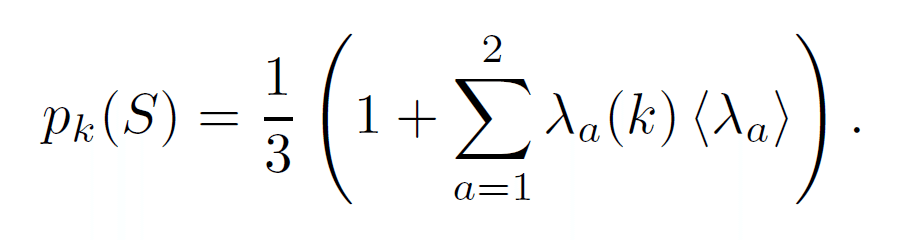
と書くこともできます。この２つの物理量については、３次元ユニタリー操作をした後にも期待値を測っています。その定義と全確率の規格化条件から３つの状態の観測確率が計算されます。ここで添え字のＵは操作をしたときの量を意味しています。
後は量子状態トモグラフィの式で密度行列を定義して、式変形をするだけです。操作をしなかった８個の期待値から下記のように初期状態の密度行列を定義します。
すると自動的に下記の関係式も成り立つことが示せます。
この式を先の１０個の期待値に関する２本の関係式の右辺に代入しましょう。
行列のトレースの線形性と、（１）式のSU(3)群の関係式を使ってやることで、以下の変形ができます。
これを先の（２）式の右辺に代入します。そしてトレースの循環性を使って次のように書きます。
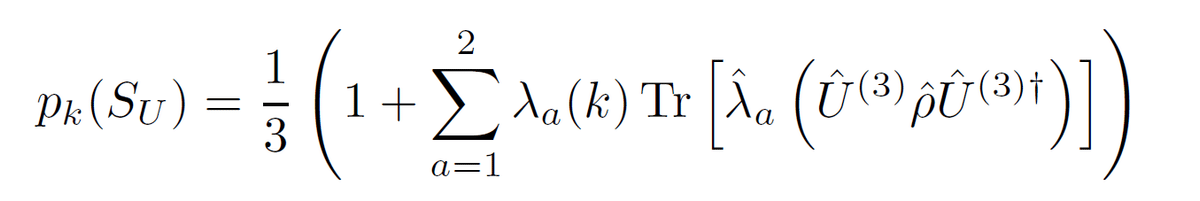
そして変形を続けます。右辺でトレースを前に出し、
とした後に、密度行列をトレース内部でくくり出します。
右辺のトレースに出てくる下記の行列は、直接計算で状態１から状態３に対応する射影行列になっています。
上の３本の式をまとめて、下の（４）式のように書きましょう
これを（３）式の右辺に代入すると、
という結果が得られます。ここで右辺のユニタリー行列を単位行列に置き換えて、密度行列を
と取れば、（５）式の確率分布は
となります。これは考えている測定が基準測定であるため、基底ベクトル|k'＞(k'=1,2,3)が状態１から状態３までに対応していることを意味しています。反復可能性があるので、この３つの状態は基準測定を使って物理的に用意できる状態です。この１つである状態１の｜１＞＜１｜を（５）式の密度行列に入れましょう。
ここに現れている３次元ユニタリー行列は物理操作によってSU(3)群の任意の元を取れるので、
で定義される複素単位ベクトルも、任意となります。そして測定での各状態の観測確率は
となることが証明されました。これがボルン則です。また同時にユニタリー行列が任意に選べることから、量子力学の状態線形重ね合わせも証明されました。
これで、確かにＸは量子系であることが実証されたことになります。つまりここで紹介した手順は未知の物体Ｘが量子力学を満たす対象であるかないかを確定させられるものだと分かりました。これは実証科学の物理学における典型的な「演繹」の例にもなっています。
結局三準位系、そしてより多くの準位をもつ系での量子力学の定式化は、第２章の二準位系の量子力学構築と同じロジックで実証科学的に達成されます。最小限の実験結果に基づいた要請から、きちんとXが量子力学的な対象であるかどうかを一意に定められます。
中平さんがブログで紹介されている、中平さんご自身の論文で前提をされているようなlocal equalityや、それと同等である局所トモグラフィ可能性という要請は、対象系と任意の外部の系との間に要請を置くため、宇宙の果てにある物理系も調べないと、その実験的な検証ができないものになっています。しかしそれだと実証科学としては自然な要請であるとは認めがたく、多くの研究者はそれに満足していません。そしてもっと実証科学として意味のある自然原理が現在探求をされています。相対論を導く相対性原理と光速度不変の原理も、きちんと実験で検証されており、そのために実証科学的にも「原理」として許容をされているのです。それと同じことを量子力学の導出でも行いたいと、その研究者達は夢見ているのです。教科書第１５章では、そのような方向性に向けたトライアルである「情報因果律」などを紹介しています。
公理や前提を最初に述べて、その帰結だけを示していくスタイルの教科書が主流ですが、そのデメリットは大きいのです。公理から予言される現象をいくら実験で確認し続けても、どの実験報告の段階からその系が本当に量子系であると断言できるかが曖昧になります。「これだけ沢山整合する実験結果もあるし、多分量子系であろう」という感じに終始してしまうのが、公理から出発する教科書の弱点です。本教科書のスタイルには、最小限これだけの実験をして理論と整合をすれば、その系は完全に量子力学という法則を満たす真の量子系であると断言できる強みがあります。
また公理系から始めるスタイルの教科書には他の問題点があって、例えば波動関数や状態ベクトルをヒルベルト空間の元だと数学的に定義してしまうことで、後々まで「その波動関数や状態ベクトルの物理的意味は、その実在性も含めて分かっていない」と読者に思わせてしまいます。このため元々は存在もしない「観測問題」の沼に読者を突き落としてしまう悲劇も起きるのです。本教科書では、その不要な迷路の入り口を完全に塞いでいます。
サポートありがとうございます。