
【量子位相推定アルゴリズム①】アダマールテスト
量子位相推定アルゴリズム
量子位相推定アルゴリズムとは、あるユニタリ行列 $${U}$$の固有値を求める量子アルゴリズムです。具体的には、ユニタリ行列$${U}$$の固有状態$${\ket{\psi}}$$に対して、
$$
U\ket{\psi} = e^{i2\pi\phi}\ket{\psi}
$$
を考えた時、この位相$${\phi}$$を推定するという問題に対応します。少し具体的な例で考えてみましょう。例えば、
$$
P = \begin{pmatrix}
1 & 0 \\
0 & e^{2i\pi\phi} \\
\end{pmatrix}
$$
という量子ゲートを考えます。この量子ゲートは、位相ゲートと呼ばれ、$${\ket{0}}$$には何も起こりませんが、$${\ket{1}}$$については、
$$
P \ket{1}= e^{2i\pi\phi}\ket{1}
$$
のように、位相を変えるような作用になります。特に、$${\phi=\pi/4}$$の時は$${T}$$ゲート、$${\phi=\pi/2}$$の時は$${S}$$ゲートと呼ばれたりします。さて、量子位相推定アルゴリズムでは、
$$
P \ket{1}= e^{2i\pi\phi}\ket{1}
$$
の位相$${\phi}$$を推定することができる量子アルゴリズムとなります。
大まかな原理
もう少しだけ、量子位相推定アルゴリズムの原理を説明します。ここで、位相$${\phi}$$を、
$$
\phi = 0.\phi_0\phi_1\cdots\phi_{n-1}
$$
のように2進数表記で考えます。当然、2進数なので、それぞれの桁の$${\phi_k}$$の値は0か1となります。仮に、$${n}$$量子ビットに対して、
$$
\ket{\phi_0}\otimes\ket{\phi_1}\otimes\cdots\otimes\ket{\phi_{n-1}}
$$
というような状態が得られたとします。そして、この状態を測定することで、求めたい位相を推定することができるというわけです。
もう少し具体例で考えてみましょう。例えば、$${\phi = 1/4}$$の場合、二進数表示では、$${\phi =1/4 \equiv 0.01}$$となります。つまり、$${\ket{\phi_0}\otimes\ket{\phi_1}=\ket{0}\otimes\ket{1}}$$という状態が観測される確率が高くなるようにすればいいことがわかります。同じように、$${\phi = 5/8}$$の場合、これの二進数表示は$${\phi = (5/8) \equiv 0.101}$$となり、$${\ket{\phi_0}\otimes\ket{\phi_1}\otimes\ket{\phi_2}=\ket{1}\otimes\ket{0}\otimes\ket{1}}$$という状態の観測確率が高くなるようにすればいいことがわかります。当然、2進数できれいに表示できる場合だけではありません。その場合は、最も最適な2進数表示の量子ビットの状態の観測される確率が高くなります。このようにして、所望の位相を推定することができるのです。
量子位相推定アルゴリズムの凄さ
さて、量子位相推定アルゴリズムの凄さは、どこにあるのでしょうか。それは、量子位相推定アルゴリズムを用いることで、あるユニタリ演算子の固有値やその固有状態を古典コンピュータと比較して、指数関数的に速く(多項式時間で)求めることができます。これが量子位相推定アルゴリズムの価値なのです。
そして、この量子位相推定アルゴリズムは、様々な量子アルゴリズムの中心的なサブルーチンを構成しており、例えば、ショアのアルゴリズムやHHLアルゴリズムといった重要な量子アルゴリズムを構成するうえで欠かせない要素となっています。
1量子ビットの量子位相推定: アダマールテスト
それでは、具体的に量子位相推定アルゴリズムの原理を見ていきましょう。まず、最も単純な例である、1個の量子ビットを用いた量子位相推定を考えてみます。このアルゴリズムは、アダマールテストとも呼ばれ、ユニタリ行列$${U}$$に対しての期待値
$$
\bra{\psi}U\ket{\psi}
$$
を求めることができます。さて、期待値$${\bra{\psi}U\ket{\psi}}$$を求める作業はそこまで大変なものなのでしょうか。実は、量子ビットの数が増えるにしたがって、期待値を求める計算が古典コンピュータでは、難しくなります。
例えば、$${n}$$量子ビットの場合を考えた時、$${\ket{\psi}}$$は$${2^n}$$次元のベクトルに対応します。そして、ユニタリ行列は、$${2^n\times 2^n}$$の大きさの行列として記述されます。つまり、量子ビット数$${n}$$が増えるにつれて、取り扱う演算子の大きさが指数的に増大し、古典コンピュータで期待値を求める計算を行うのは困難になるのです。
量子回路
さて、アダマールテストを実行する量子回路は、以下のような量子回路で表現されます。

基本的な構成としては、$${\ket{0}}$$に用意された1つの補助量子ビットと、$${n}$$個の量子ビットからなる量子状態$${\ket{\psi}}$$が入力されます。
さて、このアダマールテストの回路がどのように動作するかを順々に追っていきましょう。
Step1: 補助量子ビットにアダマールゲート
$$
H\ket{0}\otimes\ket{\psi} = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{\psi}
$$
Step2: 制御Uゲート
制御$${U}$$ゲートを作用させます。制御$${U}$$ゲートは、制御量子ビットが$${\ket{0}}$$の時は何も作用せず、制御量子ビットが$${\ket{1}}$$の時は、$${U}$$が作用するという量子ゲートになります。制御$${U}$$ゲートは、以下のような量子回路で表現されます。

数式的で表現すると、$${\ket{0}\bra{0}\otimes I+\ket{1}\bra{1}\otimes U}$$となります。CNOTゲートは、この$${U}$$が$${X}$$ゲートに、CZゲートは、$${U}$$が$${Z}$$になったものに対応しています。
さて話を戻しましょう。制御$U$ゲートがこの量子状態に作用すると、
$$
\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes \ket{\psi} \rightarrow \frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}+\ket{1}\otimes U\ket{\psi})
$$
となります。
Step3: 補助量子ビットにアダマールゲート
再度、補助量子ビットに対してアダマールゲートを作用させます。
$$
\frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}+\ket{1}\otimes U\ket{\psi}) \rightarrow
$$
$$
\frac{1}{2}(\ket{0}+\ket{1})\otimes\ket{\psi}+\frac{1}{2}(\ket{0}-\ket{1})\otimes U\ket{\psi}=\frac{1}{2}\ket{0}(I+U)\otimes\ket{\psi}+\frac{1}{2}\ket{1}(I-U)\otimes \ket{\psi}
$$
Step4: 射影測定
そして、補助量子ビットに対する射影測定を行います。測定の結果$${\ket{0}}$$が得られる確率$${P_0}$$は、
$$
P_0 = |\frac{1}{2}(I+U)\otimes\ket{\psi}|^2= \frac{1}{4}(\bra{\psi}+\bra{\psi}U^\dagger)(\ket{\psi}+U\ket{\psi})
$$
$$
= \frac{1}{4}(\braket{\psi|\psi}+\bra{\psi}U\ket{\psi}+\bra{\psi}U^\dagger\ket{\psi}+\bra{\psi}U^\dagger U\ket{\psi})
$$
$$
= \frac{1}{4}(2+\bra{\psi}U\ket{\psi}+\bra{\psi}U^\dagger\ket{\psi}) = \rm\frac{1}{2}(1+\rm{Re}\bra{\psi}\it U\ket{\psi}\rm)
$$
また、同様な計算を行うことで、測定の結果$${\ket{1}}$$が得られる確率$${P_1}$$も、
$$
P_1 = |\frac{1}{2}(I-U)\otimes\ket{\psi}|^2= \frac{1}{4}(\bra{\psi}-\bra{\psi}U^\dagger)(\ket{\psi}-U\ket{\psi})
$$
$$
= \frac{1}{4}(\braket{\psi|\psi}-\bra{\psi}U\ket{\psi}-\bra{\psi}U^\dagger\ket{\psi}+\bra{\psi}U^\dagger U\ket{\psi})
$$
$$
= \frac{1}{4}(2-\bra{\psi}U\ket{\psi}-\bra{\psi}U^\dagger\ket{\psi}) = \rm\frac{1}{2}(1-\rm{Re}\bra{\psi}\it U\ket{\psi}\rm)
$$
と求めることができます。そして、これらの結果を使うことで、期待値の実部を以下のように計算することができます。
$$
P_0-P_1 = \rm{Re}\it{\bra{\psi}U\ket{\psi}}
$$
虚部の計算
さらに、虚部$${\rm{Im}\it{\bra{\psi}U\ket{\psi}}}$$に関しては、最初のアダマールゲートの後、あるいは、制御$${U}$$ゲートの後に$${S^\dagger}$$ゲートを作用させることで、求めることができます。以下にその量子回路を示します。

Step1: 補助量子ビットにアダマールゲートと位相ゲート
$$
S^\dagger H\ket{0}\otimes\ket{\psi} = \frac{1}{\sqrt{2}}(\ket{0}-i\ket{1})\otimes\ket{\psi}
$$
Step2: 制御Uゲート
$$
\frac{1}{\sqrt{2}}(\ket{0}-i\ket{1})\otimes \ket{\psi} \rightarrow \frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}-i\ket{1}\otimes U\ket{\psi})
$$
Step3: 補助量子ビットにアダマールゲート
$$
\frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}-i\ket{1}\otimes U\ket{\psi}) \rightarrow
$$
$$
\frac{1}{2}(\ket{0}+\ket{1})\otimes\ket{\psi}-\frac{i}{2}(\ket{0}-\ket{1})\otimes U\ket{\psi}=\frac{1}{2}\ket{0}(I-iU)\otimes\ket{\psi}+\frac{1}{2}\ket{1}(I+iU)\otimes \ket{\psi}
$$
Step4: 射影測定
$${\ket{0}}$$が得られる確率$${P_0}$$は、
$$
P_0 = \frac{1}{4}(2-i\bra{\psi}U\ket{\psi}+i\bra{\psi}U^\dagger\ket{\psi}) = \rm\frac{1}{2}(1+\rm{Im}\bra{\psi}\it U\ket{\psi}\rm)
$$
となります。また、$${\ket{1}}$$が得られる確率$${P_1}$$は、
$$
P_1 = \frac{1}{4}(2+i\bra{\psi}U\ket{\psi}-i\bra{\psi}U^\dagger\ket{\psi}) = \rm\frac{1}{2}(1-\rm{Im}\bra{\psi}\it U\ket{\psi}\rm)
$$
と求めることができます。そして、これらの結果を使うことで、期待値の虚部を以下のように計算することができます。
$$
P_0-P_1 = \rm{Im}\it{\bra{\psi}U\ket{\psi}}
$$
以上の結果から、アダマールテストを用いることで、ユニタリ演算子$${U}$$の行列要素である$${\bra{\psi}U\ket{\psi}}$$を求めることができます。
アダマールテストと量子位相推定アルゴリズムの関係
さて、話を量子位相推定アルゴリズムに戻しましょう。上記のアダマールテストにおいて、ユニタリ演算子が
$$
U\ket{\psi} = e^{i2\pi\phi}\ket{\psi}
$$
を満たすような場合を考えます。すると、上記の結果を用いて、$${\ket{0}}$$が観測される確率$${P_0}$$と$${\ket{1}}$$が観測される確率$${P_1}$$は、
$$
P_0 = \rm\frac{1}{2}(1+\rm{Re}\bra{\psi}\it U\ket{\psi}\rm)=\rm\frac{1}{2}(1+\rm{Re}[ e^{i2\pi\phi}]\rm)=\rm\frac{1}{2}(1+cos(2\pi\phi))
$$
$$
P_1 = \rm\frac{1}{2}(1-\rm{Re}\bra{\psi}\it U\ket{\psi}\rm)=\rm\frac{1}{2}(1-\rm{Re}[ e^{i2\pi\phi}]\rm)=\rm\frac{1}{2}(1-cos(2\pi\phi))
$$
となります。これらの確率を、$${\phi}$$の値に関してプロットしたのが、以下の図です。

上図からも明らかなように、$${\phi=0.0}$$の場合は、$${P_0=1}$$となり、補助量子ビットを測定すると、確率1で$${\ket{0}}$$が観測され、$${\phi=0.1}$$の場合、確率1で$${\ket{1}}$$が観測されます。
一方で、$${\phi}$$が上記以外の値の場合、$${P_0}$$および$${P_1}$$は1にはならず、中途半端な値となります。その場合は、$${0.01<\phi<0.11}$$の範囲では、$${\ket{1}}$$が観測される確率が大きくなり、それ以外の領域では、$${\ket{0}}$$が観測される確率が大きくなります。つまり、位相$${\phi}$$の少数第1位が0に近いか1に近いかによって判定をすることができます。
それでは、$${\phi=0110011\cdots}$$のように小数$${n}$$位まで存在する場合はどうすればいいでしょうか。仮に今、位相$${\phi}$$が、
$$
\phi = 0.\phi_0\phi_1\cdots\phi_{n-1}
$$
と記述できるとします。当然、$${n=1}$$の時は、$${\phi=0.\phi_0}$$となり、先ほど説明したアダマールテストを用いることで、$${0}$$または$${1}$$を決めることができます。次に、小数第二位を求める場合を考えてみましょう。この際に便利な性質が、位相を二倍することで桁をずらすことができるということです。つまり、
$$
\phi=2\times0.\phi_0\phi_1=\phi_0.\phi_1
$$
としてから、アダマールテストによって$${\phi_1}$$の値を決めることができます。繰り上がった$${\phi_0}$$の値は、$${e^{i2\pi\phi}}$$においては、$${e^{i2\pi\phi_0.\phi_1}=e^{i2\pi.\phi_1}}$$となるので、数値としては関係なくなります。このように、小数$${n}$$位であっても、桁ずらしを行うことでアダマールテストによる位相推定を行うことができます。そしてこのような操作を実現するようなアダマールテストの量子回路が以下のようなものになります。

この回路は、先ほどのアダマールテストの回路で使用されて制御$${U}$$ゲートが、制御$${U^{2k}}$$ゲートに置き換わったものとなっています。この制御ゲートは、
$$
U^{2k}\ket{\psi} = e^{i2\pi2^k\phi}\ket{\psi}
$$
というように状態を変化させます。つまり、位相としては
$$
2^k\phi=2^k\times0.\phi_0\phi_1\cdots\phi_{n-1}=\phi_0\phi_1\cdots\phi_{k-1}.\phi_k\cdots\phi_{n-1}=.\phi_k\cdots\phi_{n-1}
$$
と桁が繰り上がります。これを用いることで、アダマールテストにより位相推定を行うことができるのです。
おまけ
Qiskitでのアダマールテストの実装
Qiskitを使ったアダマールテストの実装例を載せておきたいと思います。
①モジュールの準備
import numpy as np
import matplotlib.pyplot as plt
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile, Aer
from qiskit.visualization import plot_histogram
from qiskit.circuit import Parameter②アダマールテストのための量子回路
ここでは、制御$${U}$$ゲートが位相制御ゲートの場合を考えます。
def Had_test_CP(comp, state, theta):
# 補助量子ビット
ar = QuantumRegister(1, name = 'a')
n_qubit = 1
# |ψ>
qr = QuantumRegister(n_qubit, name = 'q')
# 古典レジスター
cr = ClassicalRegister(1, name = 'c')
qc = QuantumCircuit(ar, qr, cr)
# 補助量子ビットに対してアダマールゲート
qc.h(ar[0])
# 実部を求めるための量子回路
if comp == 'r':
if state == '0':
# 評価するユニタリ演算子: 制御位相ゲート
qc.cp(theta, ar[0], qr[0])
# 補助量子ビットに対してアダマールゲート
qc.h(ar[0])
# 測定
qc.measure(ar[0], cr[0])
elif state == '1':
qc.x(qr[0])
# 評価するユニタリ演算子: 制御位相ゲート
qc.cp(theta, ar[0], qr[0])
# 補助量子ビットに対してアダマールゲート
qc.h(ar[0])
# 測定
qc.measure(ar[0], cr[0])
# 虚部を求めるための量子回路
elif comp == 'i':
if state == '0':
# S^\dagger gate
qc.sdg(ar[0])
# 評価するユニタリ演算子: 制御位相ゲート
qc.cp(theta, ar[0], qr[0])
# 補助量子ビットに対してアダマールゲート
qc.h(ar[0])
# 測定
qc.measure(ar[0], cr[0])
elif state == '1':
# S^\dagger gate
qc.sdg(ar[0])
qc.x(qr[0])
# 評価するユニタリ演算子: 制御位相ゲート
qc.cp(theta, ar[0], qr[0])
# 補助量子ビットに対してアダマールゲート
qc.h(ar[0])
# 測定
qc.measure(ar[0], cr[0])
return qc実際に量子回路を出力してみましょう。
theta = Parameter('θ')
qc_real_list = [Had_test_CP(l, '0', theta) for l in ['r', 'i']]
fig, axes = plt.subplots(1, 2)
qc_real_list[0].draw('mpl', ax = axes[0])
qc_real_list[1].draw('mpl', ax = axes[1])
qc_img_list = [Had_test_CP(l, '1', theta) for l in ['r', 'i']]
fig, axes = plt.subplots(1, 2)
qc_img_list[0].draw('mpl', ax = axes[0])
qc_img_list[1].draw('mpl', ax = axes[1])
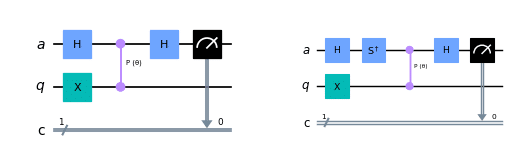
③Tゲートの場合
ここでは例として、$${T}$$ゲートの場合を考えてみます。$${\ket{0}}$$の場合は明白なので、$${\ket{1}}$$の場合のみを考えてみます。
qc1_t_list = [Had_test_CP(k, '1', theta=np.pi/4) for k in ['r', 'i']]
fig, axes = plt.subplots(1, 2)
qc1_t_list[0].draw('mpl', ax = axes[0])
qc1_t_list[1].draw('mpl', ax = axes[1])④シミュレータによる実行
この量子回路を実際に、シミュレータで実行してみます。
shots = 2**15
backend = Aer.get_backend('aer_simulator')
qc1_t_transpiled = transpile(qc1_t_list)
result = backend.run(qc1_t_transpiled, shots=shots).result()
counts = result.get_counts()
for i in [0, 1]:
if '0' not in counts[i].keys():
counts[i]['0'] = 0
if '1' not in counts[i].keys():
counts[i]['1'] = 0
plot_histogram(counts, title='Hadamard test', legend=['Real part', 'Imaginary part'])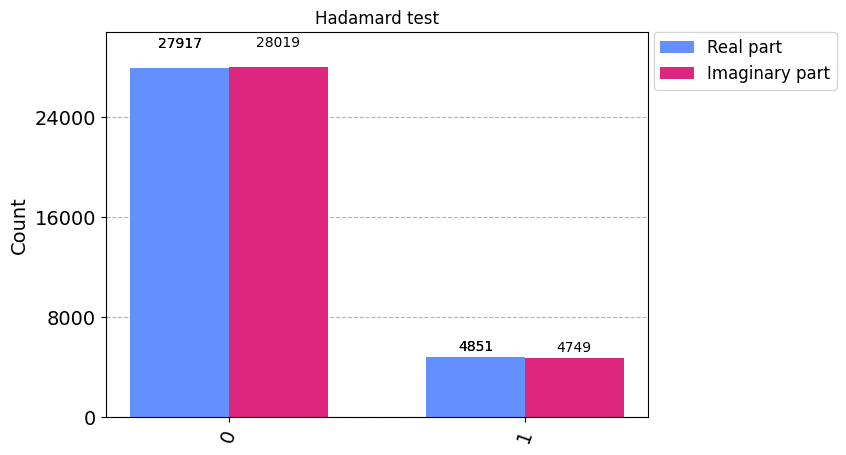
⑤理論値との比較
# 実部
# |0>を観測する確率
p0_real = counts[0]['0'] / shots
# |1>を観測する確率
p1_real = counts[0]['1'] / shots
# 実部の大きさ
real = p0_real - p1_real
# 虚部
# |0>を観測する確率
p0_img = counts[1]['0'] / shots
# |1>を観測する確率
p1_img = counts[1]['1'] / shots
# 虚部の大きさ
img = p0_img - p1_img
# 理論値
theta = np.pi / 4
phi = theta / 2 / np.pi
real_ideal, img_ideal = np.cos(2*np.pi*phi), np.sin(2*np.pi*phi)
print('Real part (simulator): {:.3f}'.format(real))
print('Real part (ideal): {:.3f}'.format(real_ideal))
print('Imaginary part (simulator): {:.3f}'.format(img))
print('Imaginary part (ideal): {:.3f}'.format(img_ideal))SWAPテスト
アダマールテストの応用例として、SWAPテストがあります。SWAPテストとは、二つの量子状態$${\ket{\psi}}$$と$${\ket{\phi}}$$の内積の大きさ$${|\braket{\phi|\psi}|^2}$$を求めることができる量子アルゴリズムです。
SWAPゲート
本題に入る前に、SWAPテストで大切になるSWAPゲートについて触れたいと思います。名前からも容易に想像できるように、SWAPゲートとは任意の2つの量子状態を交換する作用を持つ量子ゲートです。SWAPゲートは、以下のように表現されます。

さて、具体的に行列で表現するとどうなるでしょうか。$${U_{SWAP}}$$をSWAPゲートに対応する演算子とすると、
$$
U_{\rm SWAP}\ket{0}\ket{0}=\ket{0}\ket{0}=\begin{pmatrix} 1\\ 0\\ 0\\ 0 \end{pmatrix}, U_{\rm SWAP}\ket{0}\ket{1}=\ket{1}\ket{0}=\begin{pmatrix} 0\\ 0\\ 1\\ 0 \end{pmatrix},
$$
$$
U_{\rm SWAP}\ket{1}\ket{0}=\ket{0}\ket{1}=\begin{pmatrix} 0\\ 1\\ 0\\ 0 \end{pmatrix}, U_{\rm SWAP}\ket{1}\ket{1}=\ket{1}\ket{1}\begin{pmatrix} 0\\ 0\\ 0\\ 1 \end{pmatrix}
$$
となるので、
$$
U_{\rm SWAP}=\begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 \end{pmatrix}
$$
と表現することができます。
SWAPテストの量子回路
さて、SWAPテストを行う量子回路を見てみましょう。SWAPテストを実現する量子回路を以下に示します。

制御SWAPゲート
SWAPテストには、制御SWAPゲートとよばれる量子ゲートが必要となります。制御SWAPゲートとは、上記の量子回路の中央に配置された量子ゲートであり、通常のSWAPゲートとすこしだけ違う表記となっています。この制御SWAPゲートは、補助量子ビットが$${\ket{1}}$$の場合のみ、SWAPゲートが作用する量子ゲートとなります。
それではSWAPテストの詳しい動作原理について確認していきましょう。
Step1: アダマールゲート
まず、補助量子ビットに対しアダマールゲートを作用させます。
$$
H\ket{0}\otimes\ket{\psi_1}\otimes\ket{\psi_2}=\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\ket{\psi_1}\otimes\ket{\psi_2}
$$
ここからは、$${\otimes}$$は省略して表記します。
Step2: 制御SWAPゲート
補助量子ビットが$${\ket{0}}$$の場合のみ、SWAPゲートが作用。
$$
\frac{1}{\sqrt{2}}(\ket{0}\ket{\psi_1}\ket{\psi_2}+\ket{1}U_{\rm SWAP}\ket{\psi_1}\ket{\psi_2})=\frac{1}{\sqrt{2}}(\ket{0}\ket{\psi_1}\ket{\psi_2}+\ket{1}\ket{\psi_2}\ket{\psi_1})
$$
Step3: アダマールゲート
再度、補助量子ビットにアダマールゲートを作用させます。
$$
\frac{1}{\sqrt{2}}(H\ket{0}\ket{\psi_1}\ket{\psi_2}+H\ket{1}\ket{\psi_2}\ket{\psi_1})=\frac{1}{2}(\ket{0}+\ket{1})\ket{\psi_1}\ket{\psi_2}+\frac{1}{2}(\ket{0}-\ket{1})\ket{\psi_2}\ket{\psi_1}
$$
$$
=\frac{1}{2}\ket{0}(\ket{\psi_1}\ket{\psi_2}+\ket{\psi_2}\ket{\psi_1})+\frac{1}{2}\ket{1}(\ket{\psi_1}\ket{\psi_2}-\ket{\psi_2}\ket{\psi_1})
$$
Step4: 射影測定
$${\ket{0}}$$が測定される確率は、
$$
P_0 = \frac{1}{2}(1+|\braket{\psi_1|\psi_2}|^2)
$$
となり、スワップテストによって$${\ket{\psi_1}}$$と$${\ket{\psi_2}}$$の内積の大きさを評価することができることがわかります。
