
【量子コンピュータ基礎】パウリ行列
量子ビットに代表されるような二準系を記述する際に、非常に便利なツールであるパウリ行列について解説します。
パウリ行列
パウリ行列は、以下のような$${2\times 2}$$行列で表されます。
$$
\hat{\sigma}_x =
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
,
\hat{\sigma}_y =
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
,
\hat{\sigma}_z =
\begin{pmatrix}
1 & 0 \\
0 & -1 \\
\end{pmatrix}
$$
パウリ行列の性質
性質1: エルミート行列である。ユニタリ行列でもある。
行列$${\hat{H}}$$がエルミート行列であるということは、$${\hat{H}=\hat{H}^\dagger}$$が成り立つということです。ここで、パウリ行列のエルミート性は、
$$
\hat{\sigma}_x^\dagger =\hat{\sigma}_x, \hat{\sigma}_y^\dagger =\hat{\sigma}_y, \hat{\sigma}_z^\dagger =\hat{\sigma}_z
$$
が成り立つことからすぐに確認できます。
また、行列$${\hat{U}}$$がユニタリ行列であるということは、$${\hat{U}\hat{U}^\dagger=\hat{U}^\dagger\hat{U}=I}$$が成り立つということです。パウリ行列のユニタリ性は、
$$
\hat{\sigma}_x^\dagger \hat{\sigma}_x=\hat{I}, \hat{\sigma}_y^\dagger \hat{\sigma}_y=\hat{I}, \hat{\sigma}_z^\dagger \hat{\sigma}_z=\hat{I}
$$
が成り立つことから確認できます。
性質2: 交換関係
パウリ行列は、次のような交換関係を満たします。
$$
[\hat{\sigma}_x, \hat{\sigma}_y]=2i\hat{\sigma}_z,
[\hat{\sigma}_y, \hat{\sigma}_z]=2i\hat{\sigma}_x,
[\hat{\sigma}_z, \hat{\sigma}_x]=2i\hat{\sigma}_y
$$
一つだけ、例として具体的に計算してみると、
$$
[\hat{\sigma}_x, \hat{\sigma}_y]=
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
-
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
= i\hat{\sigma}_z+i\hat{\sigma}_z
= 2i\hat{\sigma}_z
$$
となり、確かに成立していることがわかります。また、上記の計算からも明らかなように、以下のような関係も満たします。
$$
\hat{\sigma}_x\hat{\sigma}_y=i\hat{\sigma}_z,
\hat{\sigma}_y\hat{\sigma}_z=i\hat{\sigma}_x,
\hat{\sigma}_z\hat{\sigma}_x=i\hat{\sigma}_y
$$
性質3: 反交換関係
パウリ行列は、次のような反交換関係を満たします。
$$
\{ \hat{\sigma}_x, \hat{\sigma}_y \} =0,
\{ \hat{\sigma}_y, \hat{\sigma}_z \}=0,
\{ \hat{\sigma}_z, \hat{\sigma}_x \}=0
$$
一つだけ、例として具体的に計算してみると、
$$
\{ \hat{\sigma}_x, \hat{\sigma}_y \}=
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
+
\begin{pmatrix}
0 & -i \\
i & 0 \\
\end{pmatrix}
\begin{pmatrix}
0 & 1 \\
1 & 0 \\
\end{pmatrix}
= i\hat{\sigma}_z-i\hat{\sigma}_z
= 0
$$
となり、確かに成立していることがわかります。
性質4: トレースに関する性質
パウリ行列は、そのトレースに関して以下のような性質満たします。
$$
{\rm Tr}[ \hat{\sigma}_x ]={\rm Tr}[ \hat{\sigma}_y ]={\rm Tr}[ \hat{\sigma}_z ]=0
$$
また、$${(\alpha,\beta=x, y, z)}$$に対して、
$$
{\rm Tr}[ \hat{\sigma}_\alpha\hat{\sigma}_\beta ]=2\delta_{\alpha\beta}
$$
が成り立ちます。ここで、$${\delta_{\alpha\beta}}$$はクロネッカーのデルタであり、下記のように記述することができます。
$$
\delta_{\alpha\beta} = \begin{cases}
1 & (\alpha=\beta) \\
0 & (\alpha\neq\beta)
\end{cases}
$$
ここまでで、パウリ行列の基本的ないくつかの性質について学んできました。ここからは、パウリ行列が関係していたり、活用されている具体的な例を紹介したいと思います。
ブロッホ球
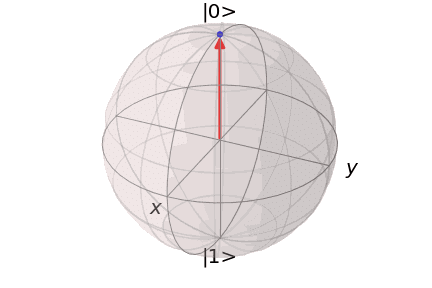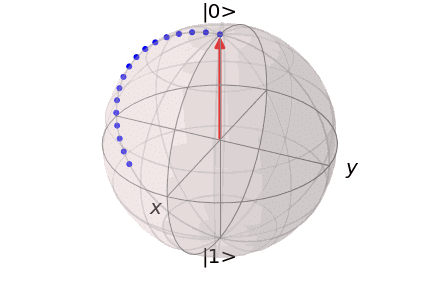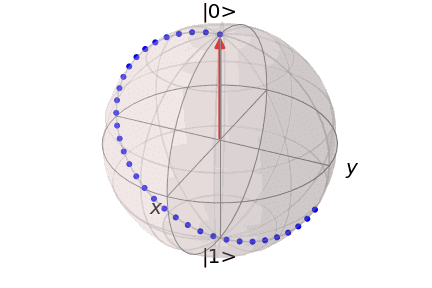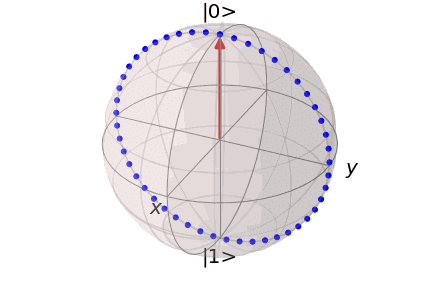
パウリ行列と量子ビットの量子状態を視覚的に表現することができる、ブロッホ球との関係について考えてみます。ブロッホ球表面上の任意の量子状態は、
$$
\ket{\psi}=\cos\frac{\theta}{2}\ket{0} +e^{i\phi}\sin\frac{\theta}{2}\ket{1}
$$
と表すことができます(下図)。

ここで、この量子状態に対するパウリ行列の期待値を計算してみると、
$$
\begin{cases}
\braket{\hat{\sigma}_x} = \bra{\psi}\hat{\sigma}_x\ket{\psi} = \sin\theta\cos\phi \\
\braket{\hat{\sigma}_y} = \bra{\psi}\hat{\sigma}_y\ket{\psi} = \sin\theta\sin\phi \\
\braket{\hat{\sigma}_z} = \bra{\psi}\hat{\sigma}_z\ket{\psi} = \cos\theta
\end{cases}
$$
となります。これらの結果は、上図のブロッホ球の図中の表記と対応していることがわかります。また、最大混合状態は、
$$
\rho_{\rm mix} = \frac{1}{2}(\ket{0}\bra{0}+\ket{1}\bra{1})
$$
と記述され、ブロッホ球では球の中心で表現されます。そして、この混合状態に対するそれぞれのパウリ行列の期待値は、
$$
\begin{cases}
\braket{\hat{\sigma}_x} = {\rm Tr}[\rho_{\rm mix}\hat{\sigma}_x] = 0 \\
\braket{\hat{\sigma}_y} = {\rm Tr}[\rho_{\rm mix}\hat{\sigma}_y] = 0\\ \braket{\hat{\sigma}_z} = {\rm Tr}[\rho_{\rm mix}\hat{\sigma}_z] = 0
\end{cases}
$$
となり、確かにブロッホ球の中心に対応していることがわかります。
回転ゲート
量子計算では回転ゲートと呼ばれるゲート操作が頻出します。この回転ゲートを理解するためには、パウリ行列の性質の理解が不可欠です。回転ゲートとは、量子ビットに対して任意の軸に関して角度$${\theta}$$だけ回転させるという操作になります。
具体的には、例えば$${x}$$軸に対する回転ゲートは、
$$
R_x(\theta)=e^{-i\frac{\theta}{2}\hat{\sigma}_x}
$$
と記述することができます。
この式は指数関数の中身が$${\hat{\sigma}_x}$$というパウリ行列になっています。結論から答えると、この指数関数は
$$
R_x(\theta)=e^{-i\frac{\theta}{2}\hat{\sigma}_x}=\cos\frac{\theta}{2}I-\sin\frac{\theta}{2}\hat{\sigma}_x=\begin{pmatrix} \cos\frac{\theta}{2} & -i\sin\frac{\theta}{2} \\ -i\sin\frac{\theta}{2} & \cos\frac{\theta}{2} \end{pmatrix}
$$
と計算することができます。この式の計算は一見複雑に見えますが、パウリ行列の性質をうまく利用することで、簡単に計算することができます。
おまけ: 導出
$$
R_x(\theta)=e^{-i\frac{\theta}{2}\hat{\sigma}_x}=\sum_{n}\frac{1}{n!}(-i\frac{\theta}{2}\hat{\sigma}_x)^n
$$
$$
=I+(-i\frac{\theta}{2}\hat{\sigma}_x)+\frac{1}{2!}(-i\frac{\theta}{2}\hat{\sigma}_x)^2+\frac{1}{3!}(-i\frac{\theta}{2}\hat{\sigma}_x)^3+\cdots
$$
$$
=I+(-i\frac{\theta}{2})\hat{\sigma}_x+\frac{1}{2!}(-i\frac{\theta}{2})^2\hat{\sigma}_x^2+\frac{1}{3!}(-i\frac{\theta}{2})^3\hat{\sigma}_x^2\hat{\sigma}_x+\cdots
$$
ここで$${{\hat{\sigma}_x^2=I}}$$より、
$$
=I+(-i)(\frac{\theta}{2})\hat{\sigma}_x+\frac{1}{2!}(-i)^2(\frac{\theta}{2})^2I+\frac{1}{3!}(-i)^3(\frac{\theta}{2})^3\hat{\sigma}_x+\cdots
$$
$$
=\sum_{n}\frac{(-i)^{2n}}{2n!}(\frac{\theta}{2})^{2n}I-i\sum_{n}\frac{(-i)^{2n}}{(2n+1)!}(\frac{\theta}{2})^{2n+1}\hat{\sigma}_x
$$
$$
=\sum_{n}\frac{(-1)^{n}}{2n!}(\frac{\theta}{2})^{2n}I-i\sum_{n}\frac{(-1)^{n}}{(2n+1)!}(\frac{\theta}{2})^{2n+1}X=\cos\frac{\theta}{2}I-i\sin\frac{\theta}{2}\hat{\sigma}_x
$$
