
【量子位相推定アルゴリズム③】
今回は量子位相推定アルゴリズムの本題に入りたいと思います。これまで、1量子ビットの量子位相推定アルゴリズムと考えることのできるアダマールテストや、量子位相推定アルゴリズムを実現するうえで不可欠な要素である量子フーリエ変換について解説してきました。今回の記事ではこれらの内容を踏まえたうえで、量子位相推定アルゴリズムの解説をしたいと思います。
量子位相推定アルゴリズム
量子位相推定アルゴリズムの量子回路図を以下に示します。
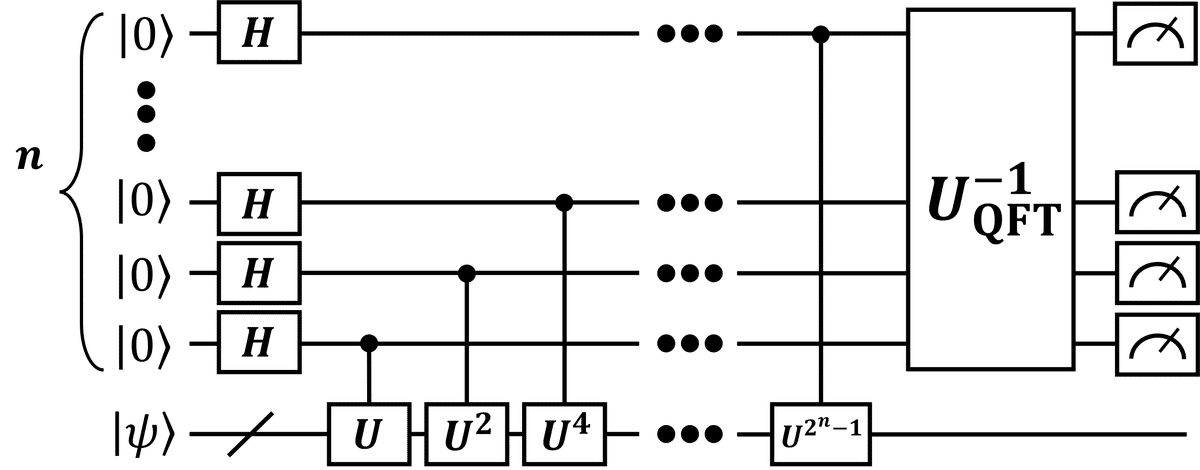
以前の記事でも解説しましたが、量子位相推定アルゴリズムとは、あるユニタリ行列$${U}$$の固有値を求める量子アルゴリズムです。具体的にはユニタリ行列$${U}$$の固有状態$${\ket{\psi}}$$に対して、
$$
U\ket{\psi} = e^{i2\pi\phi}\ket{\psi}
$$
となるとき、この固有値$${\phi}$$を推定するという問題に対応します。
大まかな原理
この量子位相推定アルゴリズムの量子回路がどのように動作するのかを簡単に解説します。
(1) 制御$${U}$$ゲートにより、位相キックバックによって位相を獲得する
(2) 獲得した位相を逆量子フーリエ変換によって計算基底ベクトルに変換
(3) 量子ビットを測定することで位相の情報を得る
という流れになっています。まだよくわかりませんね。それでは少しずつ量子回路をみていきましょう。
位相キックバック
量子位相推定アルゴリズムで重要になるのが位相キックバックです。そして、この位相キックバックは、様々な量子アルゴリズムで登場します。ここでは、位相キックバックについて簡単に解説したいと思います。位相キックバックの説明のために、次のような簡単な量子回路を考えます。

この回路がどのように動作するかを考えてみます。
(1) 初期状態
$$
\ket{0}\otimes\ket{\psi}
$$
(2) アダマールゲート
$$
H\ket{0}\otimes\ket{\psi} = \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{\psi}=\frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}+\ket{1}\otimes\ket{\psi})
$$
(3) 制御Uゲート
制御量子ビットが$${\ket{1}}$$の時だけ$${U}$$がかかるので、
$$
\frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}+\ket{1}\otimes U\ket{\psi})
$$
$$
= \frac{1}{\sqrt{2}}(\ket{0}\otimes\ket{\psi}+\ket{1}\otimes e^{i2\pi\phi}\ket{\psi}) =\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi\phi}\ket{1})\otimes\ket{\psi}
$$
という結果が得られます。この結果を見てみると、制御$${U}$$ゲートによって現れた位相が、標的量子ビットではなく、あたかも制御量子ビットについているように見えます。これが位相キックバックと呼ばれる現象です。
量子位相推定アルゴリズムにおける位相キックバック
それでは、以上の位相キックバックの説明をふまえまして、量子位相推定アルゴリズムの最初の回路の部分について考えます。

(1) 初期状態
$$
\ket{0}\otimes\ket{0}\otimes\cdots\ket{0}\otimes\ket{\psi}
$$
(2) Hadamardゲート
$$
H\ket{0}\otimes H\ket{0}\otimes\cdots H\ket{0}\otimes\ket{\psi}
$$
$$
\frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\cdots \frac{1}{\sqrt{2}}(\ket{0}+\ket{1})\otimes\ket{\psi}
$$
(3) 制御Uゲート
次に制御$${U}$$ゲートがかかります。ここで、制御$${U^{2^l}}$$ゲートは、以下の図のようなゲートに対応しています。

つまり、
$$
U^{2^l}\ket{\psi}=UU\cdots U\ket{\psi}=e^{i2\pi\phi2^l}\ket{\psi}
$$
という作用になります。そして、これらの制御$${U}$$ゲートによって生ずる位相キックバックにより、以下のような量子状態が得られます。
$$
\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi\phi2^{n-1}}\ket{1})\otimes \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi\phi2^{n-2}}\ket{1})\otimes\cdots \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi\phi}\ket{1})\otimes\ket{\psi}
$$
また、位相の部分に関して$${\phi}$$を2進数で表示、つまり
$$
\phi=0.j_0j_1\cdots j_{n-1}
$$
を用いると、
$$
\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_{n-1}}\ket{1})\otimes \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_{n-2}j_{n-1}}\ket{1})\otimes\cdots \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_0j_1\cdots j_{n-1}}\ket{1})\otimes\ket{\psi}
$$
となります。さて、この式をよくみると、
$$
\ket{j_0}\otimes\ket{j_1}\otimes\cdots\ket{j_{n-1}}
$$
を量子フーリエ変換変換した結果と等しいことがわかります。さて、この量子位相推定アルゴリズムの最終目的を再度思い出してみると、位相$${\phi}$$を求めることでした。ここで、位相$${\phi}$$は、
$$
\phi=0.j_0j_1\cdots j_{n-1}
$$
となっているため、
$$
\ket{j_0}\otimes\ket{j_1}\otimes\cdots\ket{j_{n-1}}
$$
を測定することで、位相の情報を得ることができます。つまり、上記のような量子状態を最終的に得るためには、先ほどの状態に対して量子フーリエ変換の逆の作用を与えればいいことがわかります。この操作を逆量子フーリエ変換と呼び、
$$
U_{QFT}^\dagger \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_{n-1}}\ket{1})\otimes \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_{n-2}j_{n-1}}\ket{1})\otimes\cdots \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_0j_1\cdots j_{n-1}}\ket{1})
$$
$$
=\ket{j_0}\otimes\ket{j_1}\otimes\cdots\ket{j_{n-1}}
$$
という操作になります。
逆量子フーリエ変換
逆量子フーリエ変換は、その名の通り量子フーリエ変換の逆の作用を表します。量子フーリエ変換は、
$$
U_{\rm QTF}\ket{j} = \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{i2\pi\frac{kj}{N}}\ket{k}
$$
と与えられるので、逆量子フーリエ変換は、
$$
U_{\rm QTF}^\dagger\ket{j} = \frac{1}{\sqrt{N}}\sum_{k=0}^{N-1}e^{-i2\pi\frac{kj}{N}}\ket{k}
$$
となります。つまり$${U_{\rm QTF}^\dagger U_{\rm QTF}=I}$$を満たすような操作のことです。
具体例: 2量子ビットの逆量子フーリエ変換
簡単な場合として、2量子ビットの逆量子フーリエ変換について考えてみます。まず2量子ビットの量子フーリエ変換は、

となります。逆量子フーリエ変換は、この量子回路の逆の操作に対応するので、

となります。
量子位相推定アルゴリズム
さて、量子位相推定アルゴリズムに戻ります。

この量子位相推定アルゴリズムの動作をまとめると次のようになります。上記の回路の(3)の部分で位相キックバックにより、
$$
\frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_{n-1}}\ket{1})\otimes \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_{n-2}j_{n-1}}\ket{1})\otimes\cdots \frac{1}{\sqrt{2}}(\ket{0}+e^{i2\pi0.j_0j_1\cdots j_{n-1}}\ket{1})\otimes\ket{\psi}
$$
このような量子状態が得られ、逆量子フーリエ変換により、
$$
\ket{j_0}\otimes\ket{j_1}\otimes\cdots\ket{j_{n-1}}\otimes\ket{\psi}
$$
という量子状態が得られます。そして、
$$
\ket{j_0}\otimes\ket{j_1}\otimes\cdots\ket{j_{n-1}}
$$
の部分を観測することで、位相に関する情報を得ることができます。
量子位相推定アルゴリズムの応用
さてここまで量子位相推定アルゴリズムの原理についてみてきました。そしてこの量子位相推定アルゴリズムは、様々な応用が存在しています。ここでは、この量子位相推定アルゴリズムがどういった問題に応用することができるのかについて見ていきます。
素因数分解: ショアのアルゴリズム
量子位相推定アルゴリズムの代表的な応用先の一つが、ショアのアルゴリズムです。ショアのアルゴリズムは、素因数分解を高速に行うことができる量子アルゴリズムです。素因数分解が高速にできて何が嬉しいのかという話ですが、巨大な数の素因数分解ができると、現在広く使われているRSA暗号と呼ばれる暗号技術の安全性が崩れてしまう可能性が高いのです。
このRSA暗号は、非常に大きな数の素因数分解が難しい(実行するのに時間がかかりすぎる)という事実が安全性の担保になっています。しかし、ショアのアルゴリズムを用いることで、その素因数分解の実行を古典のアルゴリズムと比較して非常に少ない計算量で実行できることがわかっています。
このショアのアルゴリズムの発見は、量子コンピュータが大きく注目される要因でもあります。ショアのアルゴリズムを含めた詳しい周辺内容は、後ほど別の記事でまとめたいと思います。
連立一次方程式 (逆行列を求める): HHLアルゴリズム
Harrow-Hassidim-Lloyd(HHL)アルゴリズムは、
$$
A {\bf x} = {\bf b}
$$
といったような線形方程式の解を、古典アルゴリズムと比較して非常に少ない計算量で求めることができる量子アルゴリズムです。実際に高速化を実現するためには、いくつかの条件をクリアすることが必要なのですが、線形方程式は機械学習や様々な物理現象のシミュレーションなど幅広い分野で登場するため非常に重要な量子アルゴリズムといえます。そしてこのHHLアルゴリズムにも、量子位相推定アルゴリズムが用いられています。
量子系のダイナミクスの計算
量子位相推定アルゴリズムは、なんらかの量子系のダイナミクスを調べる際にも有効になります。例えば、量子系のダイナミクスを記述する方程式として、シュレーディンガー方程式が知られています。この方程式は、結局のところハミルトニアンと呼ばれる物理量に対する固有値問題と最終的に落とし込むことが可能であり、ここで量子位相推定アルゴリズムの応用が期待されています。特に、古典コンピュータでは非常に多くの計算量を要する量子化学計算におけるFull-CI計算などが有名です。このあたりの話は、以前の記事でも簡単に解説しました。
