量子コンピュータが役に立つ問題(量子アルゴリズム)【量子コンピュータ入門5】

今回の記事では、量子コンピュータがどのような問題を高速に処理できるのかを説明したいと思います。

量子コンピュータにまつわる誤解

前回の記事でも述べたように、量子コンピュータにまつわる誤解の一つに、以下のようなものがあります。

量子ビットの重ね合わせ状態を用いることで、0と1の二つの値を同時に表現できる。つまり、n個の量子ビットを用いた場合には、2のn乗通りの計算パターンを同時に計算できるから計算が速い

実は、これは間違いです。この量子ビットの重ね合わせだけでは、量子コンピュータの計算速度が速くなるわけではありません。確かに、量子コンピュータは複数の計算パターンを同時に処理できるのですが、最終的に量子コンピュータの計算結果は一つの結果だけしか得ることができないという制約があります。

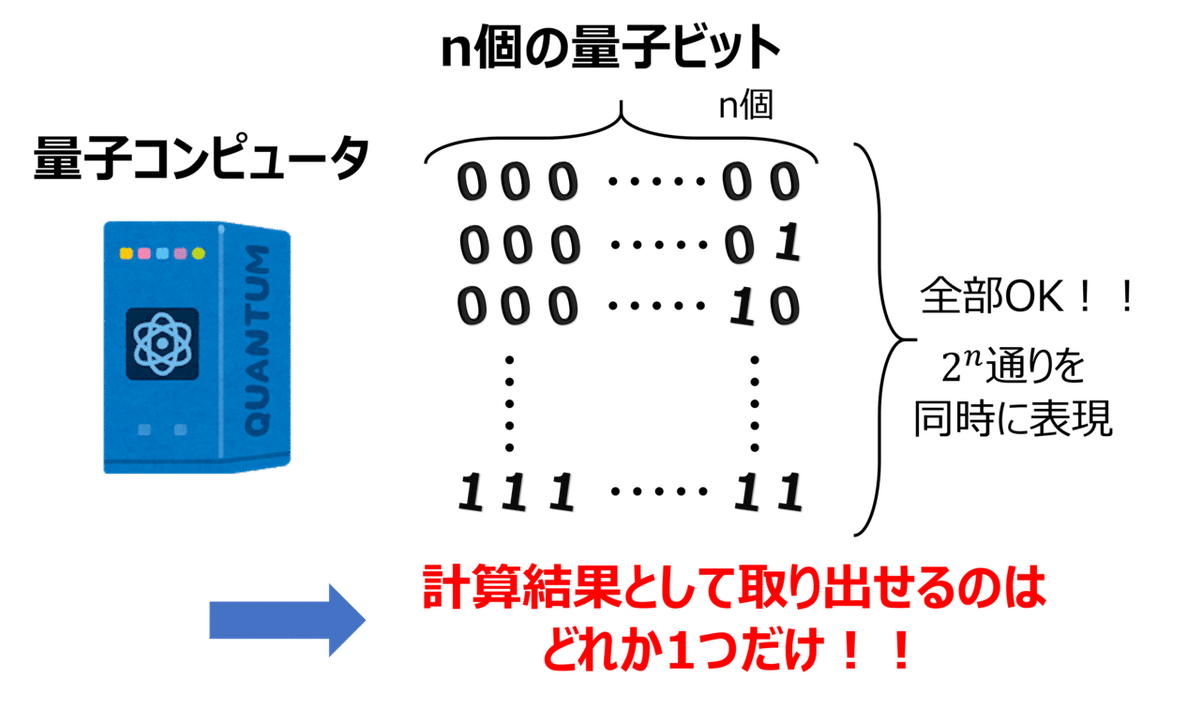
非常に沢山の計算パターンのうちの一つなので、ランダムに答えが出力されるだけになります。量子コンピュータが、特定の問題を古典コンピュータと比べて指数関数的に速く解くためには、特定の答えが得られる確率を大きくするということです。つまり、特定の答えの量子の波の大きさを増幅させることが必要になります。

波の振幅を増幅させるためには、量子干渉が必要であり、その量子干渉を上手に引き起こすためには、今回お話しする量子アルゴリズムが必要になるのです。つまり裏を返せば、良い量子アルゴリズムが見つかっている問題だけ量子コンピュータは速く処理できるという意味になります。

本記事では、量子コンピュータを使うことで古典コンピュータよりも速く(計算量を非常に少なく)解くことができる問題をご紹介しようと思います。

素因数分解問題: ショアのアルゴリズム

量子アルゴリズムでもっとも重要なアルゴリズムに、ショアのアルゴリズムがあります。ショアのアルゴリズムとは、素因数分解を高速に行うことができるアルゴリズムです。

さて、素因数分解ができることが、なぜそんなに重要なのでしょうか。

RAS暗号

それは、RSA暗号を破ることができるからです。RSA暗号とは、現代のインターネットにおける通信の安全性を担保している暗号技術です。RSA暗号は、非常に大きな数字を素因数分解することが非常に難しいということを安全性の根拠にしています。

例えば、15を素因数分解するのは簡単ですね(3×5)。それでは、84002579はどうでしょうか。

答えは、8423×9973です。かなり難しくなりましたね。このように、大きな数になればなるほどその数を二つの素数に分解するつまり、素因数分解を行うことが非常に難しくなります。

実は、非常に大きな数の素因数分解を古典コンピュータで行うと、膨大な時間がかかるのです。そして、スーパーコンピュータをもってしても、真面目に計算すると莫大な時間がかかることになり、結果として通信の安全性が担保されるということです。

しかしこれの意味するところは、もし大きな数の素因数分解が現実的な時間で実行可能になれば、インターネットにおける通信の安全性が崩れてしまうということになります。

そして、大規模な量子コンピュータは、ショアのアルゴリズムを用いることで素因数分解を古典コンピュータと比べて非常に高速に実行できることが知られています。

そこで、気になるのが量子コンピュータがRSA暗号を破ることができるのかということですね。結論から申し上げますと、それはできません。安心してください。現在の量子コンピュータでは、ショアのアルゴリズムを実行するにはまだまだ計算リソースが足りないためです。しかし将来的に、沢山の量子ビット数を搭載した大規模な量子コンピュータが登場した場合には、この限りではないでしょう。

量子探索: グローバーのアルゴリズム

次に紹介するのが、グローバーのアルゴリズムです。このアルゴリズムは、整理されていないデータベースから、特定のデータを探しだす際に用いられる探索アルゴリズムです。

具体例を出して考えてみましょう。例えば、大事なメールアカウントのパスワード4桁を忘れたとします。パスワードは、数字の0から9までの組み合わせ、つまり0000から9999までの1万通りの可能性があります。

これを、探すことを考えてみましょう。基本的には、総当たりで考えられるパスワードを打ち込んでみて、「正しい」か「正しくないか」を判定していきます。

この総当たり方式の場合、最悪の場合、0000から9999までの1万回の問い合わせで正解にたどり着くことになります。(あるいは、9999回問い合わせたら、最後の組み合わせは問い合わせなくても正しいと分かると考えても大丈夫です。)平均でも、1万回の半分の約5000回は問い合わせることが必要です。

しかし、グローバーのアルゴリズムを用いて、量子コンピュータでパスワードを探すと、なんと、100回程度の問い合わせ回数で済むのです。つまり、N回の問い合わせが必要な問題を、√N回で解にたどり着くことができるわけです。

まとめ

量子コンピュータは、良い量子アルゴリズムが見つかっている問題に関しては、高速に処理できるのです。つまり、量子コンピュータはハードウェアの研究はもちろんのこと、量子アルゴリズムの開発といった理論の研究も非常に重要なのです。

参考文献

[1]  M. A. Nielsen and I. L. Chuang, Quantum Computation and Quantum Information (Cambridge Univ. Press, 2000).
[2] 嶋田義皓 (2020) 「量子コンピューティング」 情報処理学会出版委員会 
[3] 藤井啓介 (2019) 「驚異の量子コンピュータ」 岩波書店 
[4] 武田俊太郎 (2020) 「量子コンピュータが本当にわかる!」 技術評論社