
量子計算化学プラットフォーム InQuanto 入門
(この記事は、こちらの記事の日本語訳です。)
初めに
量子化学は、物質や材料の基本的な性質を正確に記述し予測することを目的としており、新しい分子や材料の設計・開発において強力なツールです。今使われている手法は多くのユースケースで機能しますが、以下の欠点を有しています。
現在の手法は、計算の複雑さを軽減するために近似を使用しており、精度が不十分
高精度な計算手法が存在するが、スケールアップするためには大きな計算オーバーヘッドが必要であり、スパコンを用いても産業的に意味のある分子を計算できない
量子化学の計算モデリング手法として、電子密度から分子や固体のエネルギーを求める密度汎関数法(DFT)がよく利用されています。この手法は、計算コストが低く、多くの場合において比較的高精度であるため、現在では幅広く活用されています。しかし、交換相関汎関数に関して近似が必要なため、DFT では精度が足りない、ないしは、定性的に正しくない系も多く存在しています。
波動関数法は DFT よりも系統的に改良ができる可能性があり、電子相関をより正確にとらえることができると期待されている方法です。しかし、従来の古典的な計算機でこれらの方法をスケーリングさせることは、最も単純な系を除いては、困難です。例えば、最新の波動関数法である CCSD(T) は 原子の数に対して 7 乗でスケールしますが、強い電子相関を十分に表現することはできません。
量子コンピュータは、波動関数法をスケールさせることができると考えられています。この技術を使うことで、(分子や物質の)量子系を、(量子コンピュータ上の)プログラム可能な量子系にマップすることができます。波動関数を用いたアルゴリズムを効率的に実装することで、将来、大型の量子コンピュータが登場したときに、より安価に化学的精度を達成できる可能性があります。
では、なぜ今、ノイズの多い量子デバイスで化学の問題に取り組み必要があるのでしょうか?量子優位性を獲得するためのルートは単純ではなく、ハードウェアとソフトウェアの両側で改善が必要となります。今主流である、変分原理を活用した ansatz の最適化から、量子位相推定に代表されるような誤り耐性アルゴリズムへの移行は、徐々に進行していくと思われます。実際のユースケースを用いて、今からプロトタイピングを始めることは必要不可欠なプロセスです。
そのため、我々は、量子計算化学のプラットフォーム InQuanto を開発しました。このプラットフォームを通して、計算化学者から量子アルゴリズム開発者まであらゆるユーザーが、さまざまな量子デバイスを使い、最新の量子アルゴリズムと技術を簡単に利用することができます。そして、各分野における複雑な材料の化学計算における量子コンピュータの可能性を実感していただけるでしょう。
InQuanto(インクァント):量子計算化学プラットフォーム
InQuanto は Python ベースのプラットフォームであり、Jupyter 環境でプログラミングを行うことができます。InQuanto は 量子プログラミング SDK である TKET を使って実装されており、数行のコード変更で、実行する量子デバイス・シミュレータを切り替えることができます。InQuanto には、コアとなる inquanto パッケージ、その他の拡張パッケージ、及びバックエンドである TKET が含まれます。コアとなる inquanto パッケージには、量子化学計算のための最新の NISQ アルゴリズムが内蔵されています。その中には、量子化学の変分アルゴリズムの代表格である Variational Quantum Eigensolver(VQE)も含まれ、InQuanto を使うことで、簡単に実装・実行することができます。

その他にも、ADAPT-VQE、Quantum Subspace Expansion、penalty-driven VQE などさまざまなアルゴリズムが実装されています。また、Quantinuum が独自開発した、化学に特化したノイズ補正アルゴリズムも含まれています。図1は、目的となる化学の問題に対して解を得るまでのワークフローを示しています。その中には、従来の量子化学計算の問題を、サポートしている量子デバイス・シミュレータで実行できる形に変換するステップ InQuantization も含まれます。以下のセクションでは、InQuanto を使った計算事例を紹介します。
事例1:H₂ : 基底状態の計算
従来の量子化学の手法と同様、分子や固体の構造、電荷、スピン多重度、単位格子、対称性などのパラメーターを指定するところから始まります。もちろん、基底関数も選択します。大きな基底関数を使えばより正確な結果は得られますが、必要なビットや回路の深さが増えるため、量子コンピュータで実行できない可能性も出てきます。量子デバイスの進化にあわせ、コードを少し変えるだけで、常に量子デバイスを最大限有効活用することができます。
実際の物理系に対して量子計算を行うには、まず従来の量子化学計算(通常は、Hartree-Fock(HF)計算)を行う必要があります。そのため、大きな系を評価しようとする際には、古典コンピュータ上で HF 計算できるサイズの問題か、が一つのポイントとなります。InQuanto は、サードパーティ製パッケージ向けの拡張機能を有しており、PySCF やその他の可視化または量子計算のためのライブラリなど、既存のよく知られた量子化学パッケージとの連携が可能です。例えば、inquanto-pyscf パッケージを使えば、HF 計算を実行し、第二量子化されたハミルトニアン演算子を得ることができます。
典型的な次のステップは、第二量子化された演算子を適切なエンコーディングによって量子ビット演算子(=量子ビットに作用する演算子)に変換することです。InQuanto は Jordan-Wigner(JW), Bravyi-Kitaev(BK)などの複数のエンコーディングをサポートしています。デフォルトのエンコーディングは JW であり、operator.qubit_encode() メソッドは化学ハミルトニアンの第二量子化表現を量子ビット演算子に変換します。
化学系の基底状態エネルギーを計算するためには、 ansatz を定義する必要があります。InQuanto 上には 多くの ansatz が既に定義されており、すぐさま利用可能です。典型的な化学用 ansatz である UCCSD ansatz は、参照状態と、反エルミート化された UCCSD クラスタ演算子を指数とする指数関数演算子で定義されます。もし、指数も第二量子化された形であれば、そちらも対応する量子ビット演算子に変換する必要があります。 最も単純なケースでは、InQuanto の FermionSpace オブジェクトが細かい処理を代行し、一電子および二電子励起演算子を生成します。
ansatz とハミルトニアン演算子が与えられれば、express モジュールのブラックボックス関数を使って、簡単な VQE 計算をすぐに実行することができます。express モジュールを使えば、事前に計算されたハミルトニアンを即座に利用できるため、簡単に化学計算を始められます。以下の事例では、inquanto-pyscf 内の STO-3G 基底セットで事前計算された H₂ 分子のハミルトニアンを使用します。具体的には、以下のように記述できます。
from inquanto.express import load_h5, run_vqe
from inquanto.states import FermionState
from inquanto.spaces import FermionSpace
from inquanto.ansatzes import FermionSpaceAnsatzUCCSD
from pytket.extensions.qiskit import AerStateBackend
backend = AerStateBackend()
hamiltonian = load_h5("h2_sto3g.h5", as_tuple=True).hamiltonian_operator.qubit_encode()
space = FermionSpace(4)
state = FermionState([1, 1, 0, 0])
ansatz = FermionSpaceAnsatzUCCSD(space, state)
vqe = run_vqe(ansatz, hamiltonian, backend)
print("Ground state energy = ", vqe.final_value)
vqe.final_parameters.print_report()
# Ground state energy = -1.1368465754720536
# 000: s0 = 0.0000000000
# 001: s1 = 0.0000000000
# 002: d0 = -0.1072334723この例では、量子計算を行うために Qiskit ライブラリで提供される statevector シミュレーションを選択していますが、TKET を利用していることもあり、Quantinuum、IBM、Google など様々な量子デバイス・シミュレータに切り替えることが簡単にできます。
事例2:H₃⁺: 化学に特化した量子回路最適化
NISQ デバイスを最大限に活用できるよう、InQuanto は高度な技術で回路を最適化します。TKET が提供する回路最適化機能に加え、化学系に特化した手法も実装されています。
分子が特定の幾何学的対称性を示す場合、InQuanto は量子計算に必要なリソースを削減したり、エラー補正を行ったりすることができます。例えば、正三角形の三水素カチオン分子 H₃⁺ は D₃ 点群対称性を持っているため、UCCSD anstaz から励起演算子を省き、変分パラメータの数と回路の深さを減らすことができます。ユーザーが手動で対称性を指定することもできますが、inquanto-pyscf パッケージを使って、化学ドライバに任意の分子の対称性を推論するように指示することもできます。get_system() メソッドを呼び出すと、空間変数が対称性の情報を保持し、励起演算子は対称群を考慮した空間によって生成され、結果として UCCSD anstaz を使った計算において、オーバーヘッドが小さくなります。
from inquanto.extensions.pyscf import ChemistryDriverPyscfMolecularRHF
zmatrix = """
H
H 1 0.9
H 2 0.9 1 60
"""
driver = ChemistryDriverPyscfMolecularRHF(
zmatrix=zmatrix, charge=1, basis="STO-3G", point_group_symmetry=True
)
hamiltonian, space, state = driver.get_system()
from inquanto.ansatzes import FermionSpaceStateExpChemicallyAware
exponents = space.construct_single_ucc_operators(state)
exponents += space.construct_double_ucc_operators(state)
ansatz = FermionSpaceStateExpChemicallyAware(exponents, state)
from pytket.circuit import OpType
ansatz.state_circuit.depth_by_type(OpType.CX)
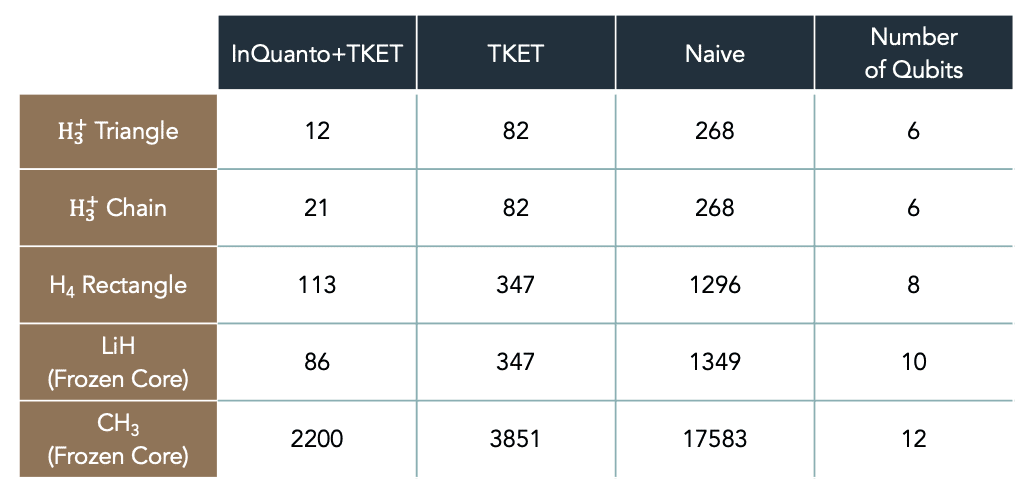
# 12対称性による回路最適化に加え、InQuanto に組み込まれた機能により、さらに回路を簡略化することができます。上記の例では、化学用の ansatz を使用し、深さが CX ゲート 12個分 の量子回路を生成しています。表1 は、いくつかの分子に対する最適化回路と非最適化回路の回路深度を示しています。上記の様々な回路最適化手法により、InQuanto ユーザーは大幅に短い量子回路を一貫して生成・利用することができます。
事例3:アスピリン:エンべディング手法
量子アルゴリズムをトイモデル系だけでなく現実的な化学の文脈でテストし実行するために、InQuanto は Density Matrix Embedding Theory(DMET)に基づくエンべディング方法をサポートしています。基本的には、分子が巨大で量子コンピュータで計算できない場合、分子を小さな断片に分割し、古典ないしは量子アルゴリズムで個別に計算するというものです。分子全体の物性は、個々のフラグメントの計算結果から導出されます。

デモとして、ここではアスピリン分子へ DMET を適用しています。図2では、分子をフラグメントに分割する方法を示しています。エンべディング手法の前に、局所的で正規化された基底を持つハミルトニアン演算子を生成する必要があり、その中で分子を空間的に分割することができます。通常、このプロセスは化学ドライバによって実行され、ドライバは完全な HF 計算を実行し、エンべディング計算を実行するために必要な1電子還元密度行列(1-RDM)を計算します。inquanto-pyscf をインストールすることで、get_lowdin_system() メソッドを通じてPySCF ドライバ を使用し、上記のハミルトニアン及び局所化された 1-RDM を生成することができます:
from inquanto.geometries import GeometryMolecular
from inquanto.extensions.pyscf import ChemistryDriverPyscfMolecularRHF
geometry = GeometryMolecular.load_xyz("aspirin.xyz")
driver = ChemistryDriverPyscfMolecularRHF(basis="sto-3g", geometry=geometry.xyz, charge=0)
hamiltonian_operator, space, rdm1 = driver.get_lowdin_system()フラグメントの定義は空間軌道に基づいて行われますが、InQuanto には使いやすさの観点から、原子によって定義されたフラグメントを空間軌道によって定義されたフラグメントに変換するユーティリティ関数 get_fragment_orbital_masks() が用意されています。inquanto-nglview は分子、軌道、フラグメントの選択と可視化に役立ちます。フラグメントの定義が完了したら、各フラグメントに対して、DMETシミュレーションを実行するための量子ソルバーを関連付けます:
from inquanto.embeddings import DMETRHF
from inquanto.extensions.pyscf import (
get_fragment_orbital_masks,
DMETRHFFragmentPyscfRHF,
DMETRHFFragmentPyscfActive,
DMETRHFFragmentPyscfFCI,
DMETRHFFragmentPyscfCCSD,
DMETRHFFragmentPyscfMP2,
)
atom_fragments = {"CH-1":[1,15], "CH-2":[3,17],
"CH-3":[2,16], "CH-4":[0,14],
"OCOH":[7,9,10,13], "CHHH":[4,18,19,20],
"OCO":[8,11,12], "CC":[5,6]}
orbsCH1, orbsCH2, orbsCH3, orbsCH4, orbsOCOH, orbsCHHH, orbsOCO, orbsCC = get_fragment_orbital_masks(driver, *atom_fragments.values() )
dmet = DMETRHF(hamiltonian_operator, rdm1)
frCH1 = DMETRHFFragmentPyscfFCI(dmet, orbsCH1)
frCH2 = DMETRHFFragmentPyscfCCSD(dmet, orbsCH2)
frCH3 = DMETRHFFragmentPyscfMP2(dmet, orbsCH3)
frCH4 = DMETRHFFragmentPyscfCCSD(dmet, orbsCH4)
frOCOH = DMETRHFFragmentPyscfCCSD(dmet, orbsOCOH)
frCHHH = DMETRHFFragmentPyscfCCSD(dmet, orbsCHHH)
frOCO = DMETRHFFragmentPyscfMP2(dmet, orbsOCO)
frCC = DMETRHFFragmentPyscfCCSD(dmet, orbsCC)
fragments = [frCH1, frCH2, frCH3, frCH4, frOCOH, frCHHH, frOCO, frCC]
result = dmet.run(fragments)InQuanto は PySCF をベースとした様々なフラグメントソルバーと、single fragment DMET、single-shot DMET、full DMET といった様々な種類の DMET をサポートしています。InQuanto はミックス&マッチを基本としているため、数多く存在する量子アルゴリズムに対するフラグメントソルバーのうち一部のみ提供しています。しかし、InQuanto では、ユーザーが独自のフラグメントソルバーを簡単に定義できるため、任意の ansazts、量子デバイス、エラー補正技術、量子アルゴリズムと DMET 法を組み合わせることができます。
class MyFragment(DMETRHFFragmentPyscfActive):
def solve_active(
self,
hamiltonian_operator,
fragment_energy_operator,
fermion_space,
fermion_state
):
... write here your quantum algorithm, for example VQE ...
return vqe_energy, fragment_energy, vqe_rdm1また、ドキュメントには、これらのフラグメント・ソルバーの作り方に関する詳細な例が記載されています。DMET は局在ハミルトニアンに依存しているため、ユーザーは化学ドライバとは別に構築した分子系や固体系のモデルハミルトニアンを使って実験することができます。
典型的なワークフロー:Reduced Density Matrix
InQuanto は、量子回路レベルまでの計算フローの低レベルコンポーネントへのアクセスを提供し、エンドツーエンドシミュレーションをフルサポートします。このように、InQuanto は、既製のメソッドで化学計算を実行するだけでなく、ユーザーが様々な計算コンポーネントを組み合わせて、カスタムワークフローを模索することも可能です。このセクションでは、従来の量子化学の経験を持つユーザーを想定し、従来の量子化学と量子計算のインターフェースを提供する、いわゆる computable を使った中級者向きの事例を紹介します。

computable は、量子デバイスを使って計算できる Reduced Density Matrix (RDM)や gradient のような高次量を意味します。しかしこれらは、VQE のような一般的な量子アルゴリズムよりシンプルである。それは、computable の場合、実際に測定する前に測定回路をすべて計算で作成することができるからである。測定回路は量子デバイス上に送られ、確率分布を取得するタイミングで、目標量を計算することができる。この計算フローを図3に示す。計算機の主な役割は、量子計測によって表現された量を計算するために、下位のサブコンポーネントを準備し、管理し、内部で最適化することである。
InQuanto がサポートする computable の一例を示すと:
基本的な computable
ExpectationValue: ある状態に対する演算子の期待値を計算する
OverlapSquared: 2つの状態の重ね合わせの2乗を計算する
複数の computable を一緒に計算する複合 computable
Computables: 任意の computable からなる tuple
ComputableList: 任意の computable からなる list
ComputableArray: 任意の computable からなる ndarray
+ - / *: computable を四則計算したものも computable
ExpectationValue を基礎とする高レイヤーの computable
ComputableRestrictedOneBodyRDM
ComputableUnrestrictedOneBodyRDM
ComputableSpinlessNBodyRDMTensor
ComputableQSEMatrices
ExpectationValueGradient
これらの computable の多くは、より高度な量子-古典ハイブリッドアルゴリズムで必要不可欠な要素です。例えば、VQE を使って基底状態を計算する時、期待値の値が最小となるように ansatz の変数を最適化します。この際、最適化の各ステップにおいて、computable を使って期待値は計算されます。
computable オブジェクトの最も基本的な例は、QubitOperator の期待値を Ansatz で表現する ExpectationValue です。
from inquanto.express import load_h5
from inquanto.ansatzes import StateTrotter
from inquanto.operators import QubitOperatorList
from inquanto.states import QubitState
from pytket.extensions.qiskit import AerBackend
backend = AerBackend()
hamiltonian = load_h5("h2_sto3g.h5", as_tuple=True).hamiltonian_operator.qubit_encode()
exponents = QubitOperatorList.from_string("theta ,[(1j, Y0 X1 X2 X3)]")
ansatz = StateTrotter(exponents, QubitState([1, 1, 0, 0]))
from inquanto.computables import ExpectationValue
energy = ExpectationValue(ansatz, hamiltonian)エネルギーはハミルトニアンの ansatz に対する期待値を意味します。最終的にエネルギーを計算するのに必要な測定回路を生成するために、測定回路をどのように生成するかについて、computable に命令する必要があります。この命令のことをプロトコルと呼び、inquanto.protocols サブモジュールから読み込むことができます。オペレーターの期待値は、さまざまな種類の測定回路で得ることができるため、InQuanto では幅広いプロトコルを提供しています。プロトコルは build() メソッドで指定し、回路を生成することができます。run() メソッドを呼ぶと、生成された回路は量子デバイスに送られ、測定が終了すると分布が取り出されます。
実行メソッドが終了すると、つまり量子コンピュータ(またはシミュレータ)から分布が取得されると、computable オブジェクトを evaluate() で評価し、その値を得ることができます。
from inquanto.protocols import ProtocolDirect
from inquanto.core import SymbolDict
protocol = ProtocolDirect()
energy.build(protocol, optimize=True)
energy.run(backend, SymbolDict(theta=0.1), n_shots = 8000)
value = energy.evaluate()また、SPAM(State Preparation and Measurement)方式や PMSV(Partition Measurement Symmetry Verification)などのエラー補正技術により、プロトコルを修正することも可能です。PMSV は化学的な対称性を利用したものであり、次のようなコードを書くことで適用することができます。
from inquanto.protocols.supporters import SupporterPMSV
symmetries = mapping.operator_map(
space.symmetry_operators_z2_in_sector(state)
)
pmsv = SupporterPMSV(symmetries)
pmsv.calibrate()
protocol = ProtocolDirect().apply(pmsv)InQuantoは、オーバーラップ、微分、computable の四則計算、または Quantum Subspace Expansion(QSE)行列やより多くの要素から構築された RDM-s など、多くの computable をサポートしています。例えば、次の例では、n 体 RDM(n=2)を計算しています。
from inquanto.states import FermionState
from inquanto.spaces import FermionSpace
from inquanto.ansatzes import FermionSpaceAnsatzUCCSD
from inquanto.mappings import QubitMappingJordanWigner
from inquanto.computables import ComputableSpinlessNBodyRDMTensor
from inquanto.protocols import ProtocolDirect
from pytket.extensions.qiskit import AerBackend
backend = AerBackend()
space = FermionSpace(4)
state = FermionState([1, 1, 0, 0])
mapping = QubitMappingJordanWigner()
ansatz = FermionSpaceAnsatzUCCSD(space, state, mapping)
parameters = ansatz.state_symbols.construct_from_array(
[0.0, 0.0, -1.07233472e-01]
)
n_body_rdm_tensor_expr = ComputableSpinlessNBodyRDMTensor(
2, space, ansatz, mapping
)
n_body_rdm_tensor_expr.build(ProtocolDirect())
n_body_rdm_tensor_expr.run(
backend,
parameters,
n_shots = 8000
)
n_body_rdm_tensor = n_body_rdm_tensor_expr.evaluate()さらに、ProtocolDirect は標準誤差の計算をサポートしているので、n_body_rdm_tensor の標準誤差を計算し、最終的な結果の誤差範囲を示すことに使えます。
n_body_rdm_tensor_std_err = n_body_rdm_tensor_expr.approximate_error()参考文献
より詳細な事例については、下記の論文をご参照ください。
Quantum Computational Quantification of Protein-Ligand Interactions
Quantum hardware calculations of periodic systems: hydrogen chain and iron crystals
Modeling Carbon Capture on Metal-Organic Frameworks with Quantum Computing
お問合せ
メール: cqcjapan.business@cambridgequantum.com (日本語 OK)
