統計的方法の基礎（連続型確率分布）

今回は統計の基礎の基礎といっても良い連続型確率分布について説明します。
QC検定の勉強をし始めたけど、全く何も分からない。
統計を勉強したこともない。
という方でも難しい式を使わずに、イメージで分かりやすく解説しますので、是非最後まで読んでもらえると嬉しいです。

連続型確率分布とは

ではまず、ここから説明します。
連続型確率分布とは、簡単に言うと

物事がどれだけの確率で起こるのかを表した線（グラフ）

です。実際に見てみましょう。

何じゃこれ？ですね。大丈夫です。順番に説明しましょう。
例えばこんなゲームをしたとします。

目を瞑ってストップウォッチを10秒ピッタリで止める

誰もがやったことがあるんじゃないでしょうか。
このゲームをたくさんの人にやってもらって結果をまとめたとします。
するとこんな感じになるはずです。

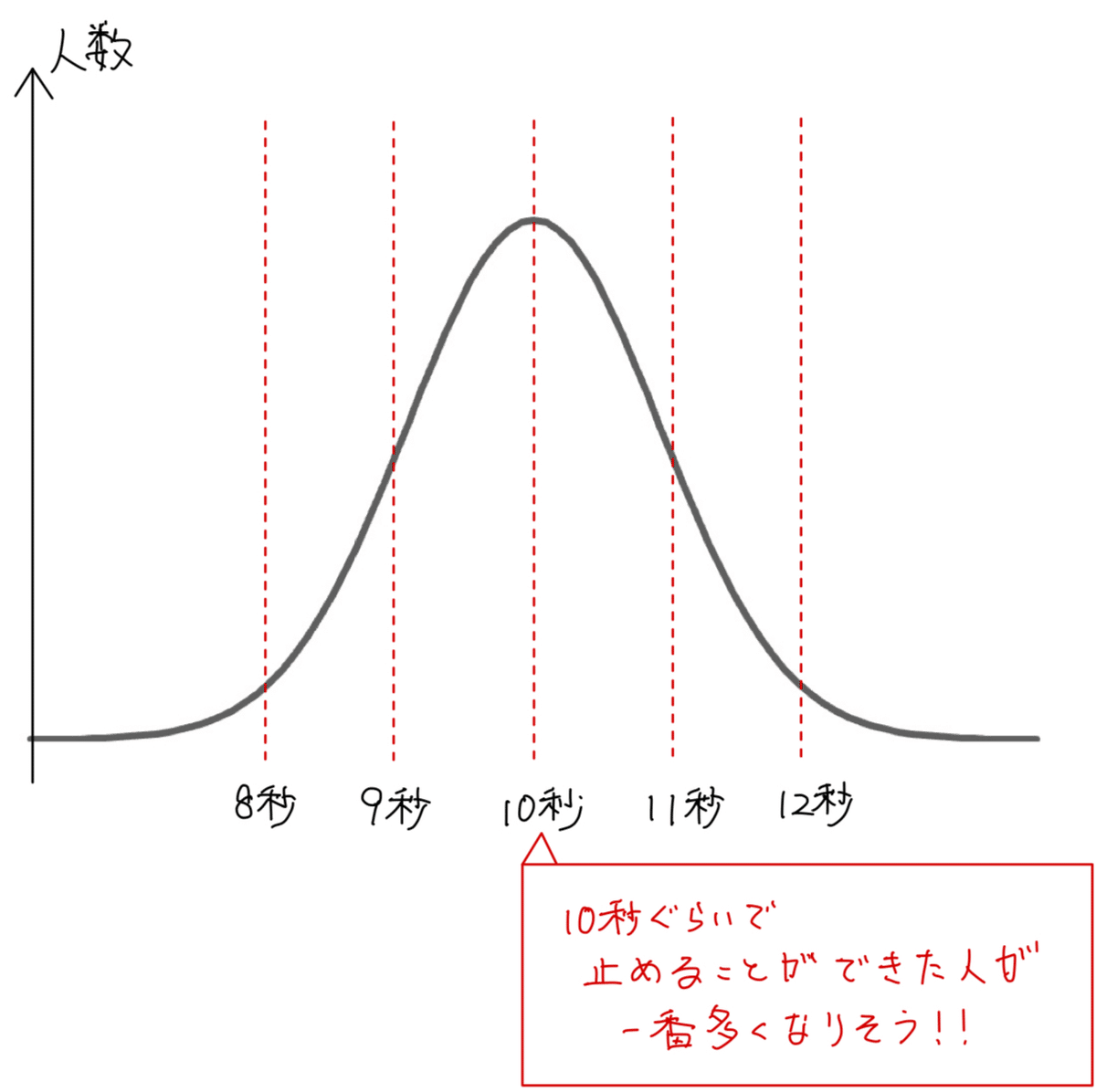
当然、10秒付近でストップウォッチを止めることが出来た人が一番多くなりそうですね。
またセンスのない人は12秒ぐらいで止めちゃう人もいそうですが、数は少なそうです。

こうしてストップウォッチを止めた人の数をグラフにしていくと、10秒を中心に左右対称のグラフができます。

何となくイメージできそうですね。


次に、このゲームを1万人にやってもらったとしましょう。

そうすると10秒以下でストップウォッチを止めた人は何人でしょうか？

そうです。だいたい5000人ですね。

何となくイメージできますよね。

グラフの縦軸は人の数を表しているので、グラフの塗りつぶしてある所がテストをした人の数。

つまり1万人です。

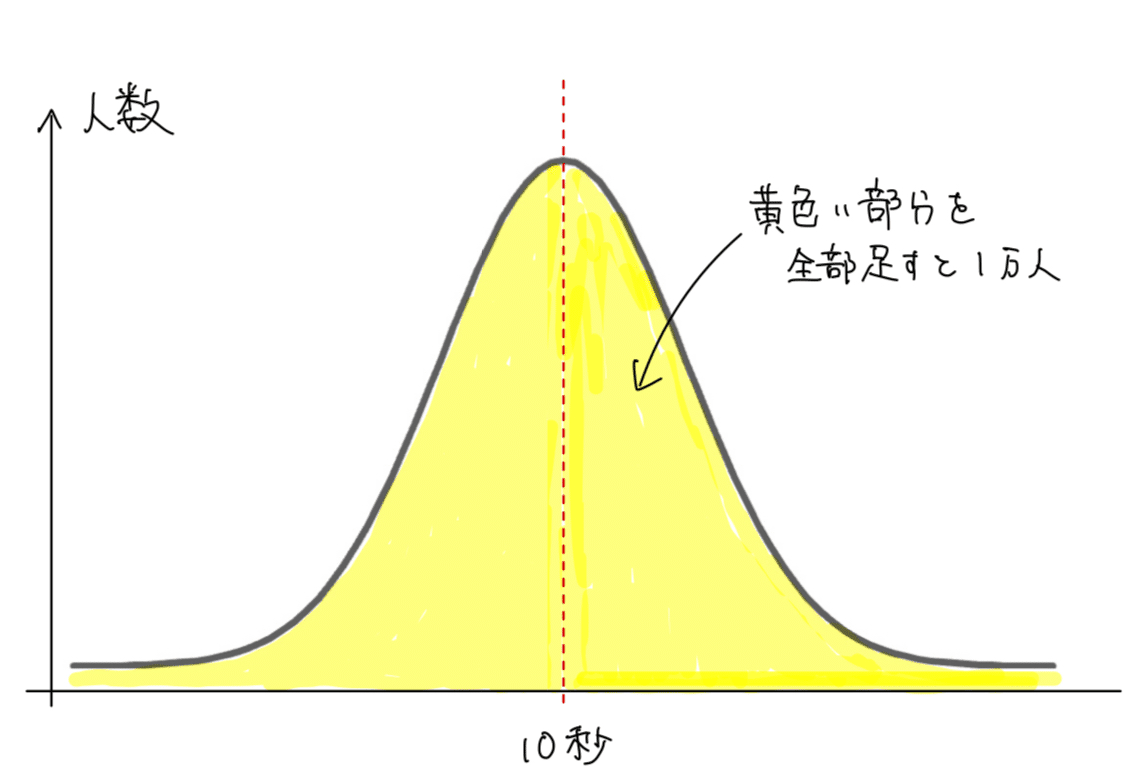
10秒以下の人の数は、グラフの左半分のことなので、1万人の半分。
これは全体の50%。
つまり5000人ですね。

次に下の図の場合を考えてみましょう。

8秒以下の黄色の部分の面積は全体の25%だとします。
8秒以下でストップウォッチを止めちゃった人（あまりセンスがなかった人）は何人でしょうか。

10,000人 × 25% = 2500人

となるわけです。

言い換えると、このゲームをやった時、8秒以下でストップウォッチを止める人が現れる確率は25%。すなわち1/4の確率って事ですね。

4人にゲームをやってもらったら、大体1人ぐらいは8秒以下で止めちゃうって事です。

つまり、塗りつぶしの部分の面積がどれぐらいか分かったら、塗りつぶしの部分の確率も分かるんですね。

ポイント1
連続型確率分布の面積は確率を表す

そしてもう一つ、このゲームをするからには気になる事があります。

そうです。

「10秒ピッタリで止めることができた人はどれだけいるのか？」

です。

気になりますね。やったからには結果を教えくれよと。そう思うでしょう。

では、結果を教えましょう。確率はゼロです。0%。

何を言ってるんだと。1万人もやったら10秒ピッタリで止める人もいるだろうと。

そう思うのは当然です。しかし違うんです。これが連続型確率分布の分かりにくいところなんですね。

では、考えてみましょう。10秒ピッタリってあり得るんでしょうか？

10秒ピッタリで止めたつもりでも、10.000001秒で止めているかもしれませんし、9.999999秒で止めているかもしれません。

つまり、単位をたくさん増やして突き詰めれば、何回ゲームをやっても、
全く同じ秒数でストップウォッチを止める事はあり得ない
って事になるんですね。

なので、10秒ピッタリで止める確率は？

と言われても、

「10秒ピッタリなんて起こらないから確率はゼロ」

になっちゃうんですね。

ポイント2
ピンポイントで確率を求める事はできない

なので連続型確率分布を使って確率を知りたいときは、範囲を決める必要があります。

今回の例で言えば、

7秒から10秒の間で止める確率は？

とか

13秒以上で止める確率は？

とかですね。

グラフにするとこんな感じ。

以上、連続型確率分布の解説でした。

今の段階では

ふーん、そんなもんかー

ぐらいで十分です。むしろ、そう思ってくれたら第一歩は大成功だったと言ってもいいでしょう。