人文地理学のための数学(2): 数理モデル
2022年3月に「人文地理学のための数学・統計学(1): 多変量解析」という記事で、人文地理学における多変量解析の利用例をいくつか紹介した。今回は、数理モデルを取りあげ、大学で学ぶ数学の知識を使ってどのようなことができるのか紹介していきたい。
人文地理学で数理モデルと聞いて、人文地理で数学?物理?と思う人もいるかもしれない。しかし、人文地理学の論文の中には数式が何十個も出てくるものもあるし、物理学のアナロジーで考案されたモデル式も実在する。
私自身も以下に紹介する数理モデル等に特段詳しいというわけではなく、内容の品質など不安な点は残るが、その点は了承願いたい。不備などがあれば随時修正していきたいと考えている。理系学部所属の大学生で人文地理学に興味のある人を中心に、関心をもち、より深く勉強する方がでてくれば幸いである。
重力モデル
重力モデル (gravity model)は、地域間流動を説明するときに用いられるモデルの1つである。地理学で研究対象となる地域間流動として、人口移動、通勤流動、貨物流動などが挙げられるが、これらの特徴をモデル式で表現しようとしている。重力モデルのモデル式は以下のように表現できる(地域i、地域jの距離をdij、人口をそれぞれPi、Pj、流動量をIij、定数をG、パラメータをbとする)。
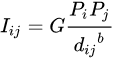
具体例を挙げて考えてみよう。東京大都市圏における通勤流動について、東京都心に視点を置けば、一般に都心に近い区市町村は遠い区市町村よりも通勤者数が多い(つまりIijが大きい)。都心に近い区市町村は遠い区市町村よりもdijの値が小さいので、b>1であれば右辺の分母の値が小さくなる、すなわち右辺の値が大きくなる。郊外に視点を置けば、距離が離れていようと東京都心への通勤者数が多いのはPjの値が大きい(ここでは「人口」は昼間人口と考えてみる)からだ、と考えてみると、具体的な事例にも適合することが理解しやすいのではないだろうか。
また、お気づきの方もいるだろうが、この式は万有引力の法則とよく似た式である。重力モデルは、万有引力の法則のアナロジーとして人文地理学、特に交通地理学で古くから用いられてきた(村山・駒木2013)。
なお、近年の地理学の研究における重力モデルの利用例として、海外送金の資金移動の要因を検討した高橋(2018)が挙げられる。
空間的相互作用モデル
重力モデルは、より広く考えると空間的相互作用モデルの1つに位置づけられる。空間的相互作用モデル (spatial interaction model)とは、地域間の流動を説明するモデルのことある。空間的相互作用モデルの一般化したモデル式は以下のように表現できる(Viは地域iの放出性、Wjは地域jの吸引性。具体例を挙げるなら、Viは発地となる地域iの人口、Wjは着地となる地域jの人口)。

すなわち、地域間流動TijをVi、Wj、dijの3変数関数で説明しようとしている。地域間の複雑な流動量を3変数関数として単純に説明できることが、空間的相互作用モデルの凄いところといえる(村山・駒木2013)。
空間的相互作用モデルの式を具体化すると、以下の式のように書ける(α、γはパラメータ、f(dij)は距離逓減関数)。

この具体化した式を見ると、重力モデルのモデル式との類似性を感じやすくなるのではないだろうか。
エントロピー最大化モデル
空間的相互作用モデルの1つにエントロピー最大化モデル (Entropy Maximizing Model)がある。エントロピー最大化モデルは重力モデルの理論的根拠を説明するなどの理論面での功績があり、教科書(例えば、村山・駒木2013)にも書かれている。
エントロピー最大化モデルの導出は、学群1年次の微積分・線形代数の内容が理解できていれば、導出の式変形も理解できるだろうと思う(「偏微分方程式」や「ラグランジュの未定乗数法」、「スターリング近似」などが前提知識となる)。杉浦(1986)、張(2011)などに記載の式を追いかけて理解していくと良いのではないかと思う。
ちなみに、エントロピー最大化モデルの導出では統計力学由来の方法が用いられている。物理学の影響を受けたモデルという意味でも重力モデルと同様だろう。
ラプラシアン
ラプラシアン (Laplacian)は、ナブラ演算子∇を2回繰り返したときの演算子である。2次元直交座標系の場合は以下の式で表される。
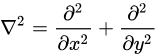
人文地理学で用いられる数理モデルでもラプラシアンが用いられるものがいくつかある。人文地理学におけるラプラシアンの利用については井上(1996)で整理されている。
ラプラシアンを用いる偏微分方程式のうち、人文地理学で最もよく用いられていたのは熱伝導方程式である(井上 1996)。熱伝導方程式は以下の式で表現される(tは時間、kは定数、fは関数)。

熱伝導方程式を用いる人文地理学関係のモデルの一例として、開拓期の人口移動を説明するHotellingモデルが挙げられる(井上 1996)。具体的な研究事例は水野(1992)などを参照してほしい。
なお、井上(1996)ではベクトル場の話で勾配や発散なども出てくる。地球基礎数学で勉強したベクトル解析を人文地理学に応用して考えてみたい方は場の理論に関する箇所も読んでみると良いかもしれない。
引用文献
井上 孝 1996. 人文地理学におけるラプラシアンの利用について. 人文地理学研究 20: 229-240.
杉浦芳夫 1986. 空間的相互作用モデルの近年の展開. 野上道男・杉浦芳夫『パソコンによる数理地理学演習』138-185. 古今書院.
高橋環太郎 2018. 太平洋の島嶼地域における2つの流動量の決定要因の比較――観光客,移民による海外送金の流動を事例に. 経済地理学年報 64: 24-35.
張 長平 2011. 空間的相互作用による地域間の人口移動分析――在日中国人を事例として. 国際地域学研究 14: 1-13.
水野 勲 1992. 開拓期の人口移動に関するHotellingモデルの再構築——非線形非平衡システムの観点から. 地理学評論 65A: 297-319.
村山祐司・駒木伸比古 2013.『新版 地域分析』古今書院.
