緯度経度からの距離の計算

こんにちは。こちらは実家待機となり、大学に行ける見通しが立っていません。

地理愛好会の定例ミーティングでの室内実験のネタとして準備していたのですが、できる見込みも立たないので、こちらで紹介することとします。

今回は、緯度経度の情報から距離を求める、をテーマにします。

地域間の距離は、地理的事象を捉えるうえで重要な要素の1つでしょう。高校地理でも立地論は出てきますし、トブラーが提唱した「地理学の第一法則」（距離が近いほど関係性が強い）も、距離と関係しています。

では、距離を求めるためには、どうすればよいでしょうか？近距離であれば、縮尺がわかっている地図に定規を当てれば良いだろうと思います。しかし、地図には歪みもありますし、完全ではありません（高緯度地域のメルカトル図法の地図を考えれば限界の存在はわかるでしょう）。

地理院地図の「計測」機能を使用すれば、簡便に高精度な値を知ることができます（使い方は 国土地理院発行の解説 を参照）。この方法も便利ですが、今回はそれ以外の方法として、緯度・経度情報をもとに距離を求める方法についてまとめてみたいと思います。

地球を完全な球体と近似する場合

今回は、地球を完全な球体と近似して、球面幾何で考えてみます。高校数学の三角比・三角関数を拡張させます。

まず、球面上で同一の大円上にない3点A, B, Cを考えます。ここで、弧BC, 弧CA, 弧ABで囲まれる領域は球面三角形といいます。弧BC, 弧CA, 弧ABの長さをa, b, cとするとき、球面余弦定理として以下の式が成り立ちます（∠A=∠CABです）。

cos a = cos b cos c + sin b sin c cos A

ここで、地球上の任意の2地点とその緯度・経度について、 P(θ1, λ1), Q(θ2, λ2) とします。

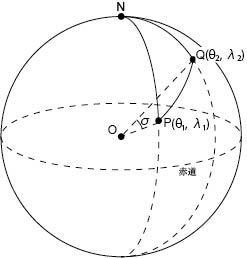
北極点をN、地球の中心をOとすると、

∠NOP= π/2 - θ1 , ∠NOQ= π/2 - θ2

ここで、球面三角形NPQを考えます。∠POQ=σ とすると、∠PNQ=λ2-λ1 なので、球面余弦定理より、

cos σ = cos (π/2 - θ1) cos (π/2 - θ2) + sin (π/2 - θ1) sin (π/2 - θ2) cos(λ2 - λ1)
      = sin θ1 sin θ2 + cos θ1 cos θ2 cos(λ2 - λ1)

よって σ = Arccos { sin θ1 sin θ2 + cos θ1 cos θ2 cos(λ2 - λ1) }

2地点間の距離をd、地球の半径をrとすると、 d=rσ が成り立つので、

d = r Arccos {sin θ1 sin θ2 + cos θ1 cos θ2 cos(λ2 - λ1)}

この式に代入すると、2地点の緯度・経度から距離を概算することができます。試しに、筑波大学筑波キャンパス（本部棟）と筑波大学東京キャンパスの距離を計算してみます。緯度・経度は以下の通り。
・筑波キャンパス 36° 6′ 41″N 140° 6′ 14″E (= 36.1114°N 140.1039°E)
・東京キャンパス 35° 43′ 10″N 139° 44′ 15″E (= 35.7194°N 139.7375°E)
ここで、 r=6370 km, θ1=0.200619 rad, λ1=0.778355 rad, θ2=0.198441 rad, λ2=0.776319 rad となるので（角度は度数法から弧度法に変換済）これを計算すると d = 54.62 km となります。

地球は完全な球体ではないのであくまで近似値ですが、三浦 (2015)を踏まえると、最終的な距離の値が有効数字2桁くらいでよければ簡便な計算方法として使えそうです（なので測量とかでは不可ですが）。

より高度な計算方法（GRS80楕円体での近似）

この他、国土地理院のサイト上で、2地点間の距離を高精度で計算することができます。このサイト (https://vldb.gsi.go.jp/sokuchi/surveycalc/surveycalc/bl2stf.html) 上では、地球をGRS80楕円体というものに近似して計算できますが、このほうが、完全な球体と近似するよりも高精度で求められます（計算式はリンク先から見られますが、かなり複雑です）。このサイト上で同様に筑波キャンパスと東京キャンパスの距離を計算すると、54.634 540 kmとなりました。なお、地理院地図の「計測」機能はGRS80楕円体近似なので、それでも同じ値が出てくると思います。

なお、国土地理院のサイト上で、緯度経度情報もいくつか公開されています。このページ (https://www.gsi.go.jp/KOKUJYOHO/center.htm) では、日本の東西南北の端の地点の緯度経度のほか、各都道府県・市町村の役所・役場や東西南北の端の地点の緯度経度がまとめられています。市町村間距離の概算で利用できそうです。

緯度経度からの距離の測定方法は色々あるので、用途にあわせて使いやすいものを選んでぜひ計算してみてください。

参考文献

三浦英俊 2015. 緯度経度を用いた3つの距離計算方法. オペレーションズ・リサーチ 60:701-705
※都市計画学者の論文ですが、地理学専攻者も参考にできそうに思います。