
格子上の連続極限と弱結合極限
場の量子論における格子正則化で疑問に思うかもしれないことについて。
(杞憂な気もします)
格子正則化において、格子間隔$${a}$$に依存する裸の結合定数$${g_0(a)}$$は$${a\rightarrow 0}$$で$${g_0(a)\rightarrow 0}$$です。しかしそうなると、連続極限をとることは弱結合極限となり、相互作用が消えてしまうように見えます。一方で連続理論において、くりこまれた結合定数$${g_R(\mu)}$$($${\mu}$$は典型的なエネルギースケール)は$${\mu}$$が小さい低エネルギー領域で$${g_R(\mu)}$$が大きくなるため摂動論が使えなくなり、クォーク・グルーオンではなくハドロンの自由度が重要になるのだ、と説明されます。ハドロン等低エネルギーの物理量の計算をするとき、格子上では連続極限をとらなければならないのに、弱結合になるとはどういうことだ?と思う人がいるかもしれません。
本記事ではこれに関して説明します。
以下自然単位系:$${c=\hbar=1}$$を採用します。
QCDは漸近自由
SU(3)のゲージ理論=量子色力学(Quantum ChromoDynamics, QCD)は漸近的自由性をもつ理論です。連続理論においてQCDの走る結合定数$${\bar g}$$を計算すると以下のようになります(Ref.[1]):
$$
\begin{aligned}
&\bar g^2(\sqrt{-q^2})=\frac{1}{\beta_0\ln( -q^2/\Lambda^2)} \tag{1},\\
&\beta_0:=\frac{1}{3(4\pi)^2}(11C_G-4N_F T_R),\\
&(C_G=3, \ N_F: \text{quarkのflavorの数}, \ T_R=1/2)
\end{aligned}
$$

ここで$${-q^2:=-(q_0^2-\vec q^2)}$$、$${q^\mu}$$はQCDのクォーク-クォーク-グルーオン 3点バーテックスに流入する4元運動量です(Fig.1。運動学的な理由で$${-q^2}$$を正とします)。$${\Lambda}$$は結合定数の$${-q^2}$$に対する依存性を決定する質量次元1の量であり「ラムダQCD」と呼ばれます。$${\Lambda}$$の値はくりこみスキームに依存しますが、連続理論では大雑把に200MeV程度です。$${N_F}$$は($${\sqrt{-q^2}}$$以下の質量の)クォークのフレーバー数です。
この結合定数はFig.1の丸の部分の「有効的な電荷」であり、クォーク・グルーオンの相互作用の有効的な強さを表します。これは系に流れ込むエネルギースケール$${-q^2}$$が大きくなると下図のように小さくなります。

つまり高エネルギー領域においてQCDは殆ど自由な粒子から構成されることを予言します。そして実際、高エネルギーの電子と陽子との非弾性的な散乱から得られるデータを解析すると、構造を持たない(殆ど)自由な粒子が陽子の中に見えます。この実験はDeep Inerastic Scattering (DIS) と呼ばれます。もうちょっとちゃんと言うと、系の構造を記述する構造関数が、高エネルギー領域で自由粒子のスケーリング則 −Bjorken scaling− を持つこと、さらにはその破れが実験で観測されています。以下はScholarpediaのBjorken scalingの項です:
細かいことは抜きにして、このリンク先の"Figure 4: Modern DIS data compared to QCD prediction"を見ると、DISの実験結果である黒丸(●)と四角(□)が、QCDの予言する線とよく一致していることがわかります。この結果は強い相互作用の基礎理論がQCDであることを強く示唆しています。
格子正則化における連続極限のとり方
話を格子上の場の理論に移します。格子正則化は、場の量子論の正則化の方法のひとつであり、時空を格子状に区切ることで発散を抑える手法です(Fig.3)。摂動論に限らず強結合・低エネルギー領域でも使える正則化であり、QCDの非摂動的な解析計算や数値計算において大変有用な方法です。

さて、QCDの数値計算である格子QCD計算において、連続極限をとることを考えます。これは隣同士の格子点の間隔$${a}$$(格子間隔)をゼロにする極限です。世の中は連続的なので、この極限を取ることが必要です。しかし$${a}$$は理論に直接現れるわけではありません。人間が勝手に用意する量です。また、格子を用意するといっても、単に4次元座標$${(x,y,z,\tau)}$$($${\tau}$$は虚時間。4次元Euclid空間で計算する)を格子点に対応させ、それを場のデータに付与するだけなので、格子間の間隔があらわに計算に現れることもないです。$${a}$$があからさまに現れないのに、どうやって$${a\rightarrow 0}$$の極限をとるのでしょうか。
今簡単のためにフェルミオンが存在しない、純ゲージ理論を考えます。このとき作用は
$$
\displaystyle
S=\sum_{n,\mu<\nu}2\beta{\rm Re}{\rm Tr}[U_{\mu\nu}(n)],\\
\beta:=1/g^2
$$
とかけます。ここで$${g}$$は理論の結合定数。$${U_{\mu\nu}(n)}$$は格子点$${n}$$におけるプラケットと呼ばれる下図で表される量です。
$$
\begin{aligned}
U_{\mu\nu}(n)&:=U_\mu(n)U_\nu(n+\hat\mu)U^\dagger_\mu (n+\hat\nu)U^\dagger_\nu(n), \\
U_\mu(n)&:=\exp(igaA_\mu(n+\hat\mu/2))
\end{aligned}
$$

太矢印が$${U_\mu}$$であり、リンク変数と呼ばれます。$${A_\mu\in {\rm su(N)}}$$はゲージ場であり、SU(N)群の代数su(N)(環)の元です。$${\hat\mu,\hat\nu}$$はそれぞれ$${\mu,\nu}$$方向の単位ベクトルです。$${U_\mu(n)}$$および$${U_{\mu\nu}(n)}$$はSU(N)の群元です。
あまり説明もなく作用を書き下しましたが、以下ではその詳細は重要ではありません。重要なのは以下の2つです:
コントロールできる理論のパラメータは結合定数$${g}$$ のみ
スケールが$${a}$$以外存在しないため、すべての物理量は$${a}$$でスケールされる(=単位のある量は$${a}$$単位で測られる)。さらに、数値計算では$${U_\mu}$$をユニットとして扱うので、$${a}$$は顕わには現れず、コントロールできない。
$${g}$$を決定する(+格子点の数および境界条件を決定する)と、すべての計算が実行できます。物理量なら何でもいいのですが、ここでは擬スカラー粒子の2点相関関数を計算します。空間座標点を$${\vec n,\vec m}$$、虚時間座標点(Euclid空間で計算します)を$${n_0, m_0}$$で表します。擬スカラー場を生成・消滅する演算子$${\hat \phi(\vec n,n_0)}$$を用意し、$${(\vec m,m_0)}$$から$${(\vec n,n_0)}$$へ伝播する相関関数を計算します。例えば
$$
\langle 0|\hat\phi(\vec n,n_0)\hat\phi^\dagger(\vec m,m_0)|0\rangle
$$
を計算します。擬スカラー粒子の生成・消滅演算子としては、例えば
$$
\hat \phi (\vec n,n_0):=\bar q(\vec n,n_0)\gamma_5 q(\vec n,n_0), \ \ \ q: クォーク場
$$
のようなものを採用し計算すればよいです($${\bar q:=q^\dagger \gamma_0}$$)。ここで一般には様々な粒子状態が中間状態として現れます。しかしながらEuclid時空では、可能な中間状態のエネルギーを$${E_i}$$とすると、各エネルギー固有状態の相関関数は$${e^{-E_i (n_0-m_0)} \ \ (n_0>m_0)}$$で落ちます。すると、$${n_0-m_0\rightarrow \infty}$$の極限では、どんな演算子を使おうが原理的には$${E_i}$$のうち最も小さなエネルギーの状態のみが残ります。これを$${E_0}$$とし、さらに$${M_0=E_0}$$とします。粒子の運動量をゼロにするため、$${\vec n}$$に関して和をとります。すると相関関数は
$$
\lim_{(n_0-m_0)\rightarrow\infty}\sum_n\langle \hat\phi(\vec n,n_0)\hat\phi^\dagger(\vec m,m_0)\rangle=B(g)\exp(-M_0(g)(n_0-m_0))
$$
になります。$${B(g)}$$は$${g}$$に依存する係数です。上の式は運動量ゼロの擬スカラーの中で最も軽い粒子が虚時間の座標点$${m_0}$$から$${n_0}$$へ伝播する確率振幅です(Fig.5):

この量を用いて連続極限をとるには以下のようにします。$${M_0(g)}$$は次元なしの量です($${n_0,m_0}$$は次元なしのただの数であることに注意)。しかし実際の粒子の質量は質量次元1です。かつ格子正則化で使える次元のある量は$${a}$$のみです。いま$${g}$$のみがコントロールできる量なので、格子間隔$${a}$$は$${g}$$に依存しているでしょう。よって質量次元1の粒子の質量を$${m_{\rm phys}}$$とすると
$$
M_0(g)=m_{\rm phys}a(g)
$$
という関係を得ます。ここで$${m_{\rm phys}}$$は物理的な実際の粒子の質量なので$${g}$$や格子点の数等には依存しない「次元を持つ定数」であるとすると、$${g}$$を調節し$${a(g)\rightarrow 0}$$となる$${g}$$において$${M_0(g)\rightarrow 0}$$になります。実際に測れるのは$${a}$$ではなく$${M_0(g)}$$なので、これがゼロになる点をもって$${a}$$がゼロになる点とします。これが連続極限です(Fig.6)。
統計力学では上記の伝播関数は相関関数と呼ばれ、$${M_0}$$は相関長$${\xi}$$の逆数に相当します。このとき、相関長が発散する点が連続極限です。これは統計力学では2次(以上)の相転移点なので「格子理論の連続極限は系のパラメタを調整して2次(以上)の相転移を起こす点に近づけることで実現される」(Ref.[2])と言えます。
$${\xi=M_0^{-1}}$$の値は、$${g}$$を変えて数値計算すると変化します。しかしこれは物理的な値が変わったわけではなく、$${a}$$が小さくなったために、$${a}$$単位で測った数値が変化したと考えます(※十分連続極限に近いとする)。例えばある$${g}$$で$${\xi=M_0^{-1}(g)=0.01}$$であり、$${g'}$$では$${\xi'=M_0^{-1}(g')=0.1}$$だったとします。このとき$${g'}$$における$${a}$$の値は、$${g}$$における$${a}$$の値の1/10です。

2つほどremarkです:
クォークの影響を含まない純ゲージ理論でも、クォークを含む演算子の相関関数は計算可能です。数値計算ではグルーオン場をモンテカルロ法で作りますが、その際にはクォークの効果は考慮しません。グルーオン場を作ったのち、2点相関関数を測るときは、そのグルーオン場を背景場にして、外場である$${q}$$を源としてその伝播を計算します。このときクォークはゲージ場の上をただ「転がる」だけです。クォークからゲージ場へのバックリアクションは存在しません。
もしかしたら、スケールパラメータの存在しない純ゲージ理論のQCDにおいて、$${a(g)}$$という関数が実現可能なことに疑問を持つかもしれません。なぜなら、次元のある$${a}$$を次元のない$${g}$$から構成するには、もうひとつ次元をもつ量を導入しそれと$${a}$$との比をとり無次元にしなければならないのに、次元をもつ量は純ゲージ理論かつ格子正則化だと$${a}$$しか無いからです。
この「もうひとつのスケール」は、現実の物理量によってもたらされます。それにより「次元転移」と呼ばれる現象を通して、$${a(g)}$$(または$${g(a)}$$)のように、次元のある量と無い量が結びつきます。詳しいことは例えばRef.[3]の「次元転移」の章をご参照ください。
以上が連続極限のとり方です。
格子正則化における結合定数と連続極限
つぎに、格子上において、結合定数$${g}$$の$${a}$$依存性$${g(a)}$$をくりこみ群方程式により計算することを考えます。
これは以下のように実行します(Ref.[3])。QCD actionに存在する結合定数を「裸の結合定数」と呼びます。いままでこれを$${g}$$で表していましたが、他の結合定数の概念と区別するため、以下これを$${g_0}$$で表します。そして格子正則化において$${g_0(a)}$$を解析的に求めます。例えばいま、クォーク間ポテンシャル$${V}$$を格子正則化および摂動論を用いて解析的に計算し、$${V(R,g_0,a)}$$を得たとします。ここでクォークと反クォークは無限に重いため場所が固定されており、その距離を$${R}$$とします(下図)。$${V}$$の計算は実際には大変ですが、それはおいておいて、とにかく$${V(R,g_0,a)}$$を得たとします。

格子正則化して$${V}$$を計算したとき、$${a}$$が十分連続極限に近いならば、$${V}$$の物理的な値は$${a}$$に依存しないでしょう。もし$${a}$$によって大きく異なるなら、$${V}$$の値など格子正則化では計算できません。そこで$${a}$$を変化させても$${V(R,g_0,a)}$$が変化しないことを要求します($${R}$$は固定)。これを実現するために、$${g_0(a)}$$のように$${g_0}$$を$${a}$$に依存させます。そして、$${V}$$の$${a}$$へのあらわな依存性と、$${g_0(a)}$$の$${a}$$依存性が打ち消されることで$${V}$$が$${a}$$に依存しないことを要求します。この条件が以下のくりこみ群方程式です:
$$
\displaystyle
a\frac{\partial}{\partial a}V(R,g_0,a)-\beta\frac{\partial}{\partial g_0}V(R,g_0,a)=0, \ \ \ \beta:=-a\frac{\partial g_0}{\partial a}
$$
上記の$${\beta}$$は「ベータ関数」と呼ばれ、結合定数の$${a}$$依存性を定める重要な量です。
摂動計算により$${g_0^4}$$のオーダーでクォーク間ポテンシャルを計算すると以下のようになります(Ref.[4] (9.8)およびRef.[5][6]。クォークループの効果は入っていない):
$$
\displaystyle
V_{q\bar q}(R,g_0,a)=-\frac{g_0^2}{4\pi R}C_2(F)
\left[1+g_0^2\frac{11N}{24\pi^2}\ln\left(7.501\frac{R}{a}\right)
+\frac{1}{4}g_0^2C_2(F)\right],\\
{}\\
(C_2(F): =(N^2-1)/N, \ \text{QCDでは}N=3)
$$
これを使って上記のくりこみ群方程式を解くと
$$
\displaystyle
g_0^2(a)=\frac{1}{\tilde\beta_0\log\left((a^{-1}/\Lambda_L)^2\right)},\ \ \ \tilde \beta_0=11/16\pi^2 \tag{2}
$$
となります($${N=3}$$とした。$${\Lambda_L}$$は質量次元1の定数。後述します)。これより
$$
a\rightarrow 0 \ において \ g_0(a)\rightarrow 0
$$
がわかります。つまりは、連続極限では裸の結合定数はゼロに近づきます。前章では$${g(a)}$$の$${a}$$依存性は議論しませんでしたが、くりこみ群の議論から「連続極限は弱結合極限($${a\rightarrow 0}$$のとき$${g_0(a)\rightarrow 0}$$という意味で)」ということがわかります。
格子上の数値計算における$${V}$$の値自体は、連続極限付近でも$${g}$$に依存して大きく変化します。しかしこれは$${V}$$の物理的な値が変化するわけではないです。$${g}$$に依存する$${a}$$の物理的な値が変化したために、$${a}$$単位で測った$${V}$$の値(これが格子上の数値計算で得られる値)が変化したのです。1mの棒を10cm単位で測れば「10」、1cm単位で測れば「100」と表せる、というのと同じです。棒の長さの表現は変化しますが、実際の長さが変化したのではなく、測る基準が変化しただけです。
連続極限のパラドックス(?)とその解決
ここまでの話で、以下のような違和感を覚える人もいるかもしれません。
最初の章で示した連続理論におけるQCDの走る結合定数は、高エネルギーになればなるほど小さくなります。逆に低エネルギー極限では結合定数が大きくなり、摂動論が使えない非摂動領域になります。低エネルギーでは結合定数が大きくなるため非摂動的効果が大きくなり、弱結合におけるクォーク・グルーオンの描像から乖離し、ハドロン=陽子、中性子、パイオン等々の自由度が現れる、とよく言います。これは正しいです。しかし一方で格子上では連続極限$${a\rightarrow 0}$$が現実世界であり、このとき結合定数はゼロになるはずです。陽子・中性子・パイオンも格子上ではこの極限で記述されるはずです。
連続理論では結合定数が大きい世界が「ハドロンの世界」、格子正則化においては結合定数が小さい世界が「ハドロンの世界」。なんとなく矛盾しているようにも感じます。(特におかしいと思わず、私の言い方がmisleadingだと思った人はそれで正しいです)
この"矛盾"の解決には、実際の物理量の計算では、$${a}$$以外のスケール$${R}$$が存在することが重要です。
確かに格子上の連続極限では、$${g_0(a)}$$が小さくなる極限を取ります。しかしそれは、物理量に対する相互作用の影響が小さくなることを意味しません。例えばクォーク間ポテンシャル$${V(R,g_0(a),a)}$$を考えます。前に述べたとおり、$${R}$$はクォーク間の距離です。確かに$${a}$$を小さくすると$${g_0(a)}$$は小さくなりますが、$${R}$$は物理的であり、これを固定すると、その間に存在する格子点は増えます。よって、連続極限の近くで$${g(a)}$$はゼロに近くなるが、しかし相互作用に与する格子点は多くなるので、結局物理量は不変になります(Fig.8)。これは結局くりこみ群方程式の思想です。
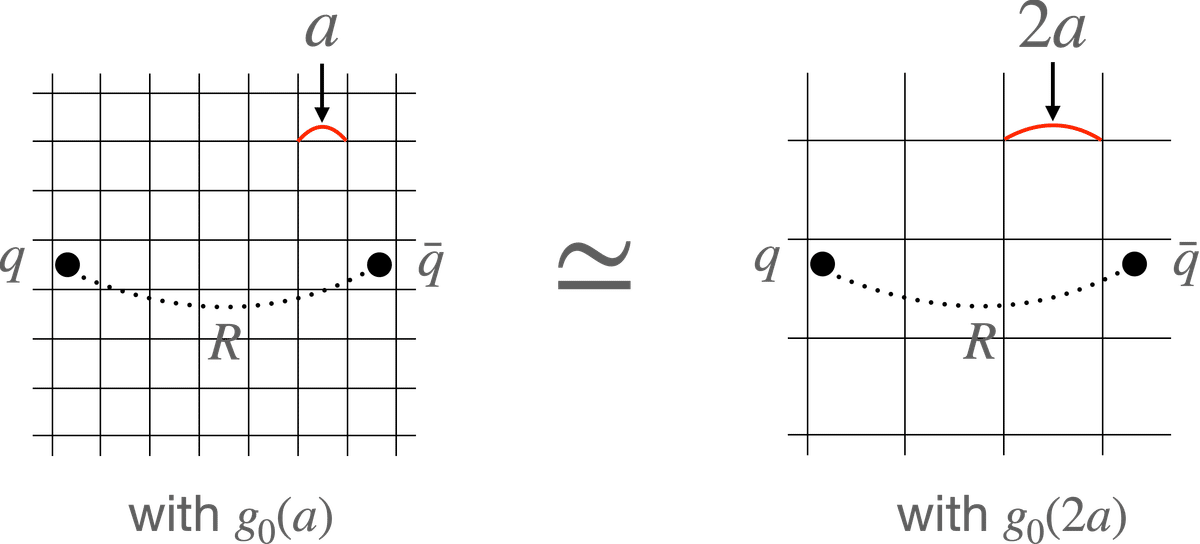
$${R}$$の具体的な値は実験値に頼ることになります。前記した粒子の2点関数の場合、$${\hat\phi}$$と同じ量子数の粒子で一番軽い粒子の質量により$${m_{\rm phys}}$$の値が定まります。$${R}$$はこの粒子のコンプトン波長くらいなので、$${R\sim m_{\rm phys}^{-1}}$$と考えられます。前に出てきた相関長$${\xi\sim M_0^{-1}}$$とは、すなわち粒子の大きさ(を$${a}$$の単位で測った値)と考えられます。$${m_{\rm phys}}$$の具体的な値と数値計算から求まった$${M_0 \ (=m_{\rm phys} a)}$$より、$${a=M_0 m_{\rm phys}^{-1}}$$が求まります。$${M_0}$$は$${g}$$に依存するので、様々に$${g}$$を変えて$${a}$$を計算すれば、$${a}$$の$${g}$$依存性が求まります。
格子上の裸の結合定数と連続極限のくりこまれた結合定数
Eq.(1)とEq.(2)は似ています。単に似ているだけではなく、Eq.(1)の$${\beta_0}$$において$${N_F=0}$$とするとEq.(2)の$${\tilde \beta_0}$$になります。Eq.(2)はクォークループの効果を考慮してないので、つまりは係数もEq.(1)とE.(2)で一致しています。
実は、「格子上の裸の結合定数$${g_0(a)}$$」と「格子正則化において連続極限+くりこみスキームを定めることで定義される『くりこまれた結合定数』$${g_r(R)}$$」に対するベータ関数は、以下のように結合定数の5次までのオーダーで同じことが示せます(Ref.[7]、P88-90):
$$
\begin{aligned}
\beta(g_0)&=\beta_0g_0^3+\beta_1g_0^5+{\cal O}(g_0^7), \ \ \ \beta(g_0):=a\frac{d}{da}g_0(a)\\
\beta_r(g_r)&=\beta_0g_r^3+\beta_1g_r^5+{\cal O}(g_r^7), \ \ \ \beta_r(g_r):=R\frac{d}{dR}g_r(R)
\end{aligned}
$$
ここで$${R}$$は前章までに現れたスケールパラメータです。よってこのオーダーで$${g_0(a)}$$と$${g_r(R)}$$は同じ形になります。
Eq.(1)は連続理論において次元正則化等(+何らかのくりこみスキーム)により計算された、くりこまれた結合定数です。Eq.(1)の$${\sqrt{-q^2}}$$を$${R^{-1}}$$と同一視すると、これは(正則化・くりこみの手法は違うけど)$${g_r(R)}$$とみなせます。
ただし、連続理論Eq.(1)の$${\Lambda}$$と格子上の理論Eq.(2)の$${\Lambda_L}$$の値は違います。これに関しては先駆的な研究としてRef.[8]があります。ゲージ群やフレーバー数やくりこみスキームにも依存しますが、$${\Lambda_L}$$は連続理論の$${\Lambda}$$の50分の1から100分の1程度であり、小さいです。
まとめ
本記事では以下を説明しました:
格子上における連続極限のとり方
格子上の裸の結合定数$${g_0(a)}$$の格子間隔依存性の導き方
連続極限$${a\rightarrow 0}$$のとき$${g_0(a)\rightarrow 0}$$になることは、物理量に対する相互作用の効果が弱まることを意味しない。$${a}$$以外の、物理的に定まるスケール$${R}$$が存在することが重要。連続極限付近では、物理量に影響する格子点が増える効果と$${g_0(a)}$$の減少の効果が相殺される。
格子上において$${a\to 0}$$でゼロになる結合定数は裸の結合定数であり、$${a}$$の関数として$${g_0(a)}$$のように記述されます。一方連続理論では、くりこみの操作によりカットオフ依存性が取り除かれます(だからこそ連続理論なのですが)。連続理論の「走る結合定数」はくりこまれた結合定数であり、格子上で言うところの$${R}$$依存性を持つ結合定数$${g_r(R)}$$に対応します。
くりこみやくりこみ群方程式は連続理論だとイマイチよくわからない人も多いと思います。一方、格子上のくりこみ・くりこみ群方程式はその思想が大変わかりやすいです。連続理論で一通り勉強してわからなかったら、例えばRef.[7]を読んで見るのも良いかもしれません。
おしまい。$${{}_\blacksquare}$$
※ヘッダ画像は「DALL・E 2」(https://openai.com/product/dall-e-2)で生成しました。
References
Mathlog記事 「走る結合定数の計算(5/5): 結合定数のrunningの決定・漸近的自由性」 (bisaitama).
青木慎也「格子上の場の理論」(Springer-Verlag Tokyo Modern Theoretical Physics Series、シュプリンガー東京).
Heinz J. Rothe, "Lattice Gauge Theories An Introduction (Third Edition)," World Scientific Lecture Notes in Physics Vol.74, World Scientific, 2005.
Eve Kovacs, "Lattice predictions for low-$Q^2$ phenomenology," Physical Review D 25 (3), 1982, pp.871-880・p.10.
U.M. Heller and F. Karsch, "One-loop perturbative calculation of Wilson loops on finite lattices," Nuclear Physics B251 (1985), pp.254-278・p.25.
Michael Creutz, "Quarks, gluons and lattices," Cambridge Monographs on Mathematical Physics, Cambridge University Press, 1983.
A.Hasenfratz and P.Hasenfratz, "The connection between the Λ parameters of lattice and continuum QCD," Phys. Lett. B 93, 165–169 (1980).
