電気から見る生理学 〜4. 生き物の電気を計算する〜
前回、細胞の外と内で、イオン濃度に勾配があるということを紹介しました。今回はイオン濃度と電気との関係について紹介していきたいと思います。
※ 2020/5/16 「電流の向き」について、追記しました
1. 濃度勾配 = 電気
そう、濃度勾配こそが電気なのです 笑
これだけではもちろん何が何だか、と思われると思います。しかし、よく考えてみてください。イオンが多い場所とイオンが少ない場所の間にある壁に穴が開いたら、イオンはどう動くでしょうか?多い場所から少ない場所へたくさん流れることが想像できるはずです。そう、これこそが電気の正体なのです!細胞膜という壁に阻まれて内外でイオン濃度は明確に異なりますが、その細胞膜にあるイオンチャネルが開くと、そこを通ってイオンが流れます。1回目の記事で、電気とは「電荷を持つ粒が動いたときに起こる現象」と紹介しました。まさに今、イオンがイオンチャネルを通って動いたので、そこに電気が生じたわけです。
2. 電気を知るための基本式①
しかし、そんな雰囲気だけを掴んでも正確な値を知ることはできません。そこで、少しだけ難しい計算式を紹介します。膜に隔たれた2つの空間において(細胞など)、その内外でのあるイオンAの濃度が分かっていて、そのイオンAが自由に膜を通過できる場合、以下のような計算式(ネルンストの式、Nernstの式)によってその膜にかかる電圧を求めることができます。
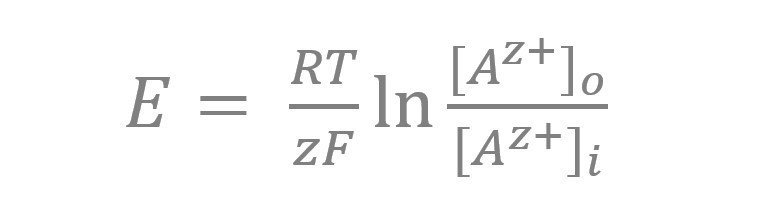
E: 電圧(V)
R: 気体定数(8.31 J/K・mol)
T: 絶対温度(K)
z: イオンの価数(単位なし)
F: ファラデー定数(9.65 × 10^4 C/mol)
(ln: 自然対数のこと)
[Az+]o: 細胞外のAz+イオン濃度(mol/L)
[Az+]i: 細胞外のAz+イオン濃度(mol/L)
それではここで計算をしてみましょう。細胞の膜電位は多くの場合、カリウムによって規定されるといわれます。というわけでカリウムについて計算してみます。
カリウムの場合、価数 = 1(1+)、細胞内が150 mM(= 0.15 mol/L)、細胞外が4 mM(= 0.004 mol/L)の濃度ですので、体温(37℃ = 310 K)で計算するとおおよそ-0.0968 V (= -96.8 mV)になります。
この意味は、濃度差が150 mMと4 mMにキープできれば、37℃では、その膜は-96.8 mVを示す(外側が0 mV, 内側が-96.8 mV)、ということです。この回で紹介したトランスポーターのおかげでこの濃度差は保てています。細胞外の電位を 0 mV とする、というのは決まりなので、この際は割り切ってください。
注釈:
細胞内外の濃度差を形成したのは、確かにトランスポーターですが、「トランスポーターがないと膜電位は生み出されない」というのも、実は誤りです。例えば、脂質二重膜で細胞を模倣したもの(リポソーム)を作り、その膜上にカリウムしか通さないカリウムチャネルを置いて、その内外のカリウム濃度を150 mM・4 mMにしてやれば、やっぱり膜電位は-96.8 mVになります。どうしてかというと、濃度勾配に従ってカリウムイオンが内側から外側に移動すると、カウンターイオン(Clイオンなど)は移動できないので、移動したカリウムイオン分だけ内側が負電荷を持つようになり、カリウムイオンが外に行く力が抑えられるためです。そしてこの、濃度勾配によって外に出る力と、電気勾配によってそれが妨げられる力が釣り合って、イオンの動きが見かけ上ゼロになる点こそが、平衡電位なのです。
ここで、よくご存じの方は何かがおかしいことに気付くと思います。一般的な静止膜電位とは-60~70 mVを指すと言われますが、明らかにカリウムの逆転電位はそれよりも深くなります。これはすなわち、一般的にはカリウムが膜電位を決めるとされますが、他のイオンも実は微妙に効いている、ということを意味しています。実際、塩化物イオンやナトリウムイオンも、カリウムイオンほどではありませんが膜電位を動かすことが知られています。
3. 電気を知るための基本式②
そんな、複雑なイオン同士の関係を捉えるためには、以下のゴールドマン-ホジキン-カッツの式(Goldman-Hodgkin-Katzの式、GHK式)を用います。

Px: イオンXの膜での透過係数(相対値)
ほとんどネルンストの式と同じですが、今回は生体で重要なナトリウム・カリウム・塩化物イオンだけが出てくるようになっています。Pは透過係数と呼ばれ、簡単に言うとイオンがどれくらい膜を通過しやすいかを示します。一般的に、細胞における透過係数はおおよそPK : PNa : PCl = 1 : 0.04 : 0.45 のようですので、上と同じように37℃(= 310 K)、各濃度はこの回で紹介したもので計算してやると、-76.8 mVになります。おおよそですが、近づきました。
ここで覚えていてほしいことは、カリウムチャネルは常に開いている、ということです。カリウムの逆転電位は、通常膜電位よりも深いので、基本的にはずっとカリウムイオンが内から外へ出続けています。ですので、膜電位はカリウムの影響をとても受けやすいのです。カリウムを静脈注射するとヒトが簡単に死ぬのも、このあたりに原因があります(他のイオンも大概、静脈注射は危ないですが)。
4. 電流の正負はどうやって決まる?
さて、上ではずっと電圧の話をしてきましたが、最後に電流についても、軽く触れたいと思います。基本的に、電流の流れる向きは、電圧の勾配で決まります。電圧の高い方から低い方に流れるのです。平衡電位が 0 mV の陽イオンが作る電流を考える際、細胞内が100 mV なのなら、電流は内から外へと流れますし、細胞内が -100 mV なのなら、電流は外から内へと流れます(このとき、上で述べた通り細胞外は 0 mV としています)。
では、「正の電流」は、細胞内から外へ出る電流のことなのでしょうか?それとも、細胞外から細胞内へ入る電流のことなのでしょうか?
膜を流れる電流は、オームの法則に従って、以下の計算式で解くことができます。
(膜電位) - (平衡電位) = (膜電流) × (膜抵抗)
∴ (膜電流) = 1/(膜抵抗) × {(膜電位) - (平衡電位)}
平衡電位を膜電位から引くのは、膜電位 = 平衡電位のとき、電流は 0 になるからです(数学でいう、グラフの平行移動の考え方と同じです)。上の例の場合、膜電位が 100 mV・平衡電位が 0 mV のとき、電流は内から外へ流れますが、この時の値を計算すると、膜電流は正になります(膜抵抗は常に正としてください)。つまり、外向きの電流が正の電流です。膜電位が負の時も同様の計算をしてもらえれば、内向きの電流が負の電流、とわかるかと思います。
というわけで、理論的にはこのように電流の向きは決まりますが、基本的にどんなイオンや膜電位であっても、この「外向き電流が正の電流」は覆りませんので、覚えてしまっても良いです。ただし、電流とイオンの流れる向きは、同一とは限りませんので、ご注意ください(陽イオンの流れる向きと電流が一緒、陰イオンの流れる向きと電流は逆、です)。
それでは今回はこのあたりで。
読んでいただいてありがとうございました!
いいなと思ったら応援しよう!