
オプション取引入門 知識編②の補足ーボラティリティの計算
オリジナルの記事はこちら。
これまでオプションの基本を説明するにあたって、何度も「ボラティリティ」という言葉が出てきました。ボラティリティは「原資産の値動きの大きさ」であるとざっくりした意味合いで使われておりましたが、そもそもそれは統計学において、どのように正確に定義されているものなのでしょうか。そして金融の世界でボラティリティといった場合、原資産の変動の大きさという他にどのような解釈が可能なのでしょうか。本稿ではそれらの点について補足します。
まずは原資産の変動の大きさとして、ボラティリティというものを数式抜きで直感的におさらいしておきましょう。皆さんは価格の変動の大きさと聞いてまず何を思い浮かべるでしょう。
少しボラティリティという用語に慣れ親しんだ人だとまず下のような株価のヒストリカルデータの動きを考えた人もいるかもしれません。

たしかに株価はずっと一方的な方向にではなく、毎日上にも下にも「変動」していますね。それゆえ株価は全体として「ジグザグ」に動いているように見えます。このジグザグの度合いが株価の変動率の大きさであり、ボラティリティなのです。
ですがこの「ジグザグの度合い」という量を正確に統計学という学問の中で記述した場合どうなるでしょう。
まずは、例えばより局所的な値動きを取り出して、以下のような値動きを考えてみましょう。

こういった値動きにおける株価の平均をと考えると下の赤線の水準になります。

この「平均値と毎日の株価がどれだけ離れているか」がつまりは価格変動の大きさ、しいては「ジグザグの度合い」、つまりはボラティリティということになります。

株価の変動率が大きい場合、それぞれの矢印が大きくなり、その絶対値をすべて足すと大きな値になります。逆に株価の変動率が小さい場合、矢印の合計の大きさは小さな値になります。
実際統計学におけるボラティリティとはこの矢印の大きさの合計で表現できます。以下に数式としてのボラティリティの定義を載せておきます。

さて、上の式の右辺の平方根の中身にあたる、各々の矢印の2乗の和のことを統計学では「分散」と呼びます。これも価格変動を表すものですが、一般にボラティリティというと、この分散の正の平方根である「標準偏差」のことを指します。もし株価の動きが正規分布に従うとすると、標準偏差は次の地点において株価がおよそ67%の確率でその中に収まるような範囲を意味します。標準偏差がそのような分かりやすい意味合いを持つために、株価の変動率の大きさであるボラティリティは分散ではなく標準偏差で表現されることが多いわけです。例えば、年率のボラティリティが20%であれば「だいたい67%の確率で来年の株価は今の株価の+-20%の範囲にいる」と解釈することができるわけです。
最後にボラティリティの具体的な計算をしてみましょう。
以下は11/29から12/3までの日経平均株価の動きです。その期間の日経平均株価のリアライズドボラティリティを実際に計算します。
まずは5日分の日経平均株価の分散を求めます。
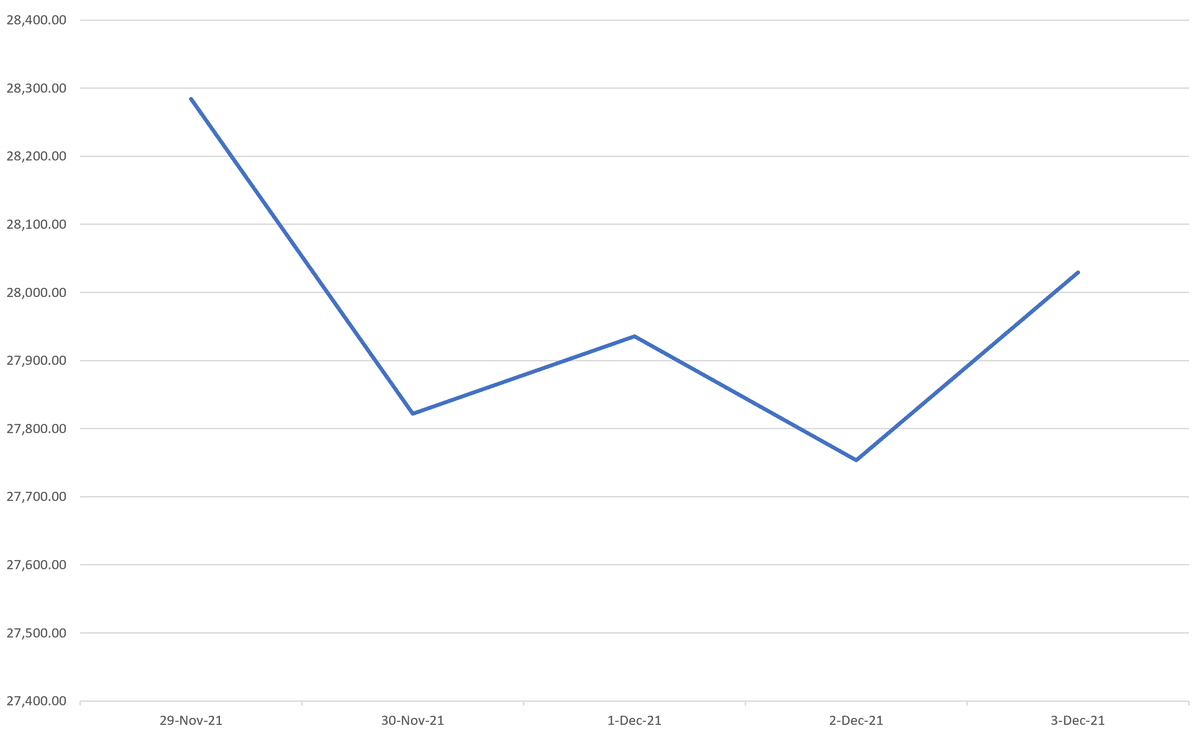
上のグラフの値動きは下のグラフのようになるので、

これらの値動き(%)の平均値はおよそ-0.2204となります。
それぞれの日の価格について平均値との差の二乗を計算すると以下の表のようになります。

これらの平均値を計算すると、0.0001014でありこれが分散です。さらにこの正の平方根をとると0.0100735となるので、標準偏差はおよそ1%ということになります。
ボラティリティは年率換算され表されるのが一般的であるので、上の標準偏差を再び分散に直し、年率換算しボラティリティを求めると、以下のようになります。
まず、一年間に営業日数は大体245営業日あります。
標準偏差は平方根を計算したものなので線形性がないので、1%を二乗して分散に戻し、から245をかける必要があります。
なので0.0245の正の平方根をとると、約15.65%と計算できます。
これで日経平均の5日間の値動きから求めた、年率のリアライズドボラティリティは15.65%と求まりました。これが意味するのは先にも述べた通り、5日間の日経平均の動きから推測するに、一年後には株価が今の+-15.65%になっていることがだいたい67%の確率で期待されるということです。(もちろん任意のz%において一年後に株価が+-z%になっている確率ももちろん計算することができます。正規分布表というものがそのような確率を与えてくれます)
ボラティリティは金融資産の中でもその原資産によってかなり異なるので注意が必要です。例えば日経平均だとだいたい15%-20%くらいのあいだに収まることが多く、S&P500であれば10%-15%といったところでしょうか。またFXのUSD/JPYだと5%とか10%ぐらいになり、株式の世界よりもずっとボラティリティは小さいです。ボラティリティが大きい資産の代表としては仮想通貨があげられます。ビットコインのボラティリティは小さくても50%、大きい時で100%を越える時もあるでしょう。
