
#3 マチコ先生とニャー助のデータサイエンス 「データの可視化ってなにニャ?」編: Rバージョン 全20講
都内の某ネコカフェ
マチコ先生: ねえ、ニャー助、今日はいい天気だね。
ニャー助: うんニャ、気持ちいいニャ!散歩に行きたいニャ。
マチコ先生: そうだね。でも、今日はデータサイエンス講座の第三回目があるから、それを終えてから散歩に行こうね。
ニャー助: そうだニャ!データサイエンス講座って面白いニャ。マチコ先生が教えるから、すぐに理解できるニャ。
マチコ先生: ありがとう、ニャー助。さて、話を戻そうね。今日はデータの可視化について話そう。データの可視化は、世間話のように、情報をわかりやすく伝えることが大事だよ。
ニャー助: 世間話とデータの可視化がどう関係してるニャ?
マチコ先生: 世間話では、相手が興味を持って話を聞くために、わかりやすく伝えることが大事だよね。データの可視化も、データを理解しやすく伝える方法だから、似ているんだ。
ニャー助: なるほどニャ!じゃあ、データの可視化を学んで、データをわかりやすく伝えられるようになりたいニャ!
マチコ先生: いいね、ニャー助。それじゃあ、始めようか。最初に散布図について説明するね。
基本手法その1:散布図って・・なにニャ?
マチコ先生: 散布図は、2つの変数の関係を可視化するのに使われるよ。具体的には、変数間の相関や分布、外れ値の確認に役立つんだ。例えば、学生のテストの点数と勉強時間の関係を見ることができるよ。
ニャー助: なるほどニャ。じゃあ、Rのコードとフェイクデータで教えてニャ!
マチコ先生: もちろん!フェイクデータを作ってみようね。例えば、5人の学生がいて、それぞれのテストの点数と勉強時間がこうなっているとするよ。
test_scores <- c(60, 75, 85, 90, 95)
study_hours <- c(2, 5, 8, 10, 12)
これで、テストの点数と勉強時間の関係を散布図で表示できるよ。
plot(study_hours, test_scores)
ニャー助: おお!散布図を見ると、勉強時間が長いほど、テストの点数が高くなる傾向があることがわかるニャ!
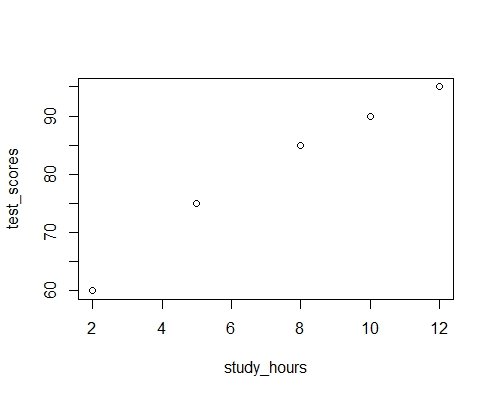
マチコ先生: そうだね、ニャー助。散布図を使うと、データの傾向や関係性が一目でわかるから、非常に便利だよ。また、データの外れ値や異常値も見つけやすくなるんだ。
ニャー助: 素晴らしいニャ!でも・・・ニャー助は初心者なりよ。Rのコードの一行ごとにコメントをつけて、それぞれ何やってるか、説明してほしいニャ。
マチコ先生: もちろん、ニャー助。コメントをつけて説明するね。
# テストの点数を格納するベクトルを作成
test_scores <- c(60, 75, 85, 90, 95)
# 勉強時間を格納するベクトルを作成
study_hours <- c(2, 5, 8, 10, 12)
# 勉強時間とテストの点数の関係を散布図で表示
plot(study_hours, test_scores)ニャー助: なるほどニャ!コメントがあると、どの行が何をやっているかわかりやすいニャ!
マチコ先生: そうだね、ニャー助。コメントを書くことで、自分自身や他の人がコードを読むときに理解しやすくなるよ。今後もコードを書くときは、コメントをつける習慣をつけていこうね。
ニャー助: うんニャ!これからは、コメントを書くことを大切にするニャ!そしてこれからも散布図を活用して、データを理解しようニャ!でもほかに手法はあるのかニャ?
基本手法その2:折れ線グラフってなにニャ?
マチコ先生: 折れ線グラフがあるわよ、ニャー助。折れ線グラフは、時系列データや連続したデータの変化を示すのに役立つよ。例えば、ある地域の過去5年間の気温の変化を見ることができるよ。
ニャー助: なるほどニャ。じゃあ、Rのコードとフェイクデータで教えてニャ!コメントもお願いニャ。
マチコ先生: いいね!過去5年間の平均気温をフェイクデータとして作ってみようね。
# 過去5年間の年ごとの平均気温を格納するベクトルを作成
average_temperatures <- c(15, 16, 15.5, 17, 16.5)
# 年のラベルを格納するベクトルを作成
years <- c(2018, 2019, 2020, 2021, 2022)
# 年ごとの平均気温の変化を折れ線グラフで表示
plot(years, average_temperatures, type = "l")
ニャー助: 折れ線グラフで、過去5年間の気温の変化が一目でわかるニャ。
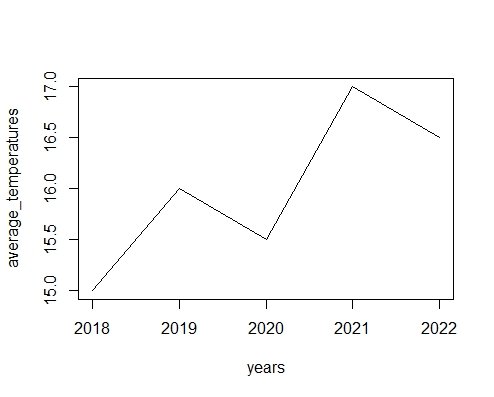
マチコ先生: そうだね、ニャー助。折れ線グラフは、時間の経過とともにデータがどのように変化しているかをわかりやすく示すことができるから、非常に便利だよ。今後もさまざまな場面で折れ線グラフを活用してね。
ニャー助: ありがとうニャ、マチコ先生!折れ線グラフを上手に使えるようになるニャ!でも・・・散布図と折れ線グラフのほかに可視化の手法ってあるのかニャ?
基本手法その3:棒グラフってなにニャ?
マチコ先生: あるわよ、ニャー助。棒グラフはよく使うわね。
ニャー助: 棒グラフ・・聞いたことはあるけど、これについても、具体的にどういった場面で使うか、どうして使われるのか教えてほしいニャ。
マチコ先生: もちろん、ニャー助。棒グラフは、カテゴリ別のデータを比較するのに役立つよ。例えば、4つの異なる果物の売り上げを比較することができるよ。
ニャー助: なるほどニャ。じゃあ、Rのコードとフェイクデータで教えてニャ!コメントもお願いニャ。
マチコ先生: いいね!4つの果物の売り上げをフェイクデータとして作ってみようね。
# 4つの果物の売り上げを格納するベクトルを作成
sales <- c(120, 150, 100, 180)
# 果物の名前を格納するベクトルを作成
fruits <- c("Apple", "Banana", "Grape", "Orange")
# 果物ごとの売り上げを棒グラフで表示
barplot(sales, names.arg = fruits)
ニャー助: おお、棒グラフで、果物ごとの売り上げの違いが一目でわかるニャ。
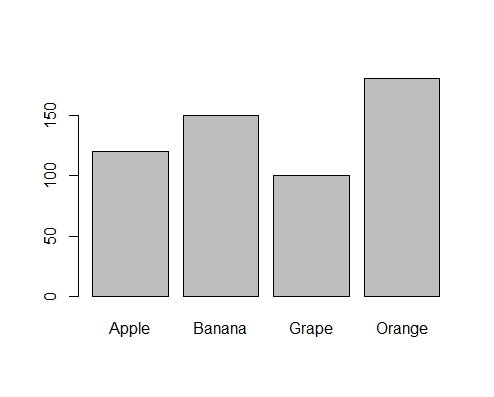
マチコ先生: そうだね、ニャー助。棒グラフは、カテゴリごとのデータを直感的に比較できるから、非常に便利だよ。今後もさまざまな場面で棒グラフを活用してね。
ニャー助: ありがとうニャ、マチコ先生!棒グラフを上手に使えるようになるニャ!
応用手法その1:ペアプロット
ニャー助:もうこれで、ニャー助はデータ可視化のプロだニャ!
マチコ先生:(まだ早いわよ)うん、基本はそれでいいんだけど、データ可視化はまだまだ奥が深いわよ。例えば多変数データの可視化ってどうするかわかる?
ニャー助:おお、分からんニャ!ニャー助は思い上がっていたみたいだニャ・・・。そしたら多変数データの可視化についても教えてほしいニャ。
マチコ先生: もちろん、ニャー助。多変数データの可視化では、ペアプロットやヒートマップがよく使われるよ。今回は、ペアプロットについて説明するね。ペアプロットは、複数の変数の組み合わせごとに散布図を作成して、変数間の関係を一度に確認できるよ。
ニャー助: なるほどニャ。じゃあ、Rのコードとフェイクデータで教えてニャ!コメントもお願いニャ。
マチコ先生: いいね!フェイクデータとして、4種類の花の大きさと形状を測定したデータを作ってみようね。
# 必要なライブラリをインストール
install.packages("GGally")
# ライブラリを読み込む
library(GGally)
# フェイクデータを作成(4種類の花の大きさと形状)
flower_data <- data.frame(
size = c(1.2, 1.5, 1.8, 2.0, 3.0, 3.2, 3.5, 3.8, 4.0, 4.5),
shape = c(2.0, 2.1, 2.3, 2.5, 3.0, 3.1, 3.3, 3.5, 3.6, 3.8),
type = factor(c(rep("A", 5), rep("B", 5)))
)
# 多変数データをペアプロットで可視化
ggpairs(flower_data)
ニャー助: おお!ペアプロットで、花の大きさと形状の関係が一目でわかるニャ。
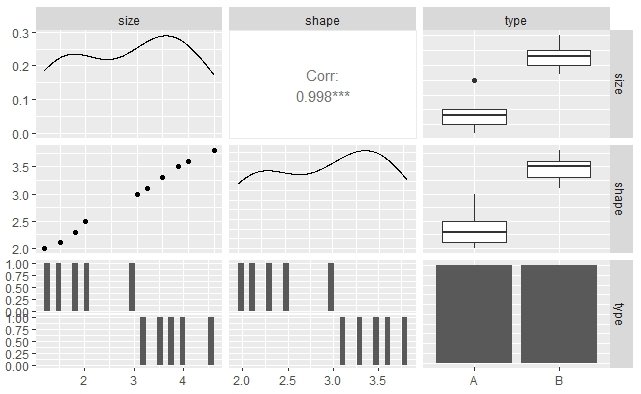
ニャー助: ペアプロットで9種類のグラフが出てきたけど、それぞれどう解釈したらいいにゃ?
マチコ先生: ペアプロットで9種類のグラフが出てくるのは、3つの変数がそれぞれの組み合わせでプロットされるからだね。それぞれのグラフの解釈について説明するよ。
ニャー助: ありがとニャ!教えてほしいニャ。
マチコ先生: まず、対角線上のグラフはヒストグラムで、それぞれの変数の分布を示しているんだ。これによって、各変数がどのような範囲の値を取るのか、また分布の形状がどうなっているのかを把握できるよ。
次に、対角線より上のグラフと下のグラフは、それぞれの変数の組み合わせごとの散布図を示しているんだ。これらのグラフを見ることで、2つの変数間の関係や傾向を調べることができるよ。例えば、正の相関や負の相関があるか、または特定のグループ間で傾向が異なるかどうかを観察できるね。
ニャー助: なるほどニャ!対角線上は各変数の分布を見るためで、対角線より上と下は2つの変数間の関係を調べるためなんだニャ。
マチコ先生: そうだね!ペアプロットは、複数の変数間の関係や分布を一度に見ることができるので、データの全体像を把握するのに役立つよ。ただし、ペアプロットでは3次元以上の関係は表現できないので、その点は留意してね。今後もさまざまな場面で多変数データの可視化を活用してね。
ニャー助: ありがとうニャ、マチコ先生!多変数データの可視化を上手に使えるようになるニャ!ほかに「お主、通よのう」って思われるテクはないかニャ?
マチコ先生:(お主って古っ。時代劇?)そうだね、ニャー助。ヒートマップがあるよ。
ニャー助:ヒートマップ面白そう!教えてほしいニャ
応用手法その2:ヒートマップ
マチコ先生: もちろん、ニャー助。ヒートマップは、データの密度や強度を色で表現することで、視覚的にわかりやすくする方法だよ。例えば、商品の売り上げの地域別の違いを見ることができるよ。
ニャー助: なるほどニャ。じゃあ、Rのコードとフェイクデータで教えてニャ!
マチコ先生: いいね!フェイクデータとして、地域別の商品A、B、Cの売り上げデータを作ってみようね。
# 必要なライブラリをインストール
install.packages("gplots")
# ライブラリを読み込む
library(gplots)
# フェイクデータを作成(地域別の商品A、B、Cの売り上げデータ)
sales_data <- matrix(c(100, 120, 150,
80, 95, 110,
130, 90, 75),
nrow = 3,
byrow = TRUE)
# 行名(地域名)と列名(商品名)を設定
rownames(sales_data) <- c("Region1", "Region2", "Region3")
colnames(sales_data) <- c("ProductA", "ProductB", "ProductC")
# 売り上げデータをヒートマップで可視化
heatmap.2(sales_data, trace = "none", col = colorRampPalette(c("white", "red"))(10))
ニャー助: なるほど~ヒートマップで、地域別の商品売り上げの違いが一目でわかるニャ。でもどうやって解釈したらいいにゃ?
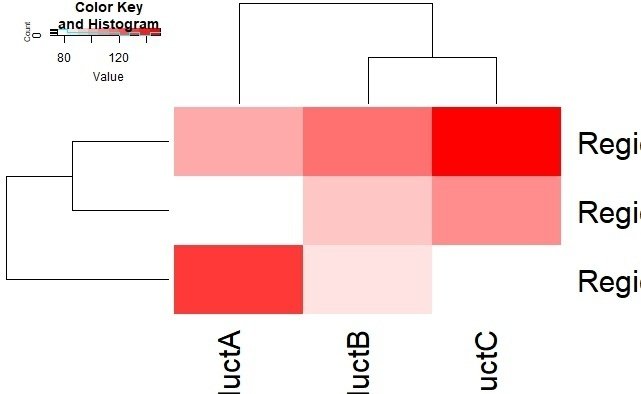
マチコ先生: ヒートマップは色を使って、2つのカテゴリ変数間の数値データの強弱を表現するグラフだよ。ヒートマップの解釈について説明するね。
ヒートマップでは、横軸と縦軸にそれぞれカテゴリ変数を置いて、セルの色で数値データを表現するんだ。色が濃いほど、そのセルの値が大きいことを意味しているよ。逆に、色が薄いほど、そのセルの値が小さいことを示しているね。
ヒートマップを解釈する際には、まず色の濃淡がどのように分布しているかを観察することが大切だよ。特定のカテゴリ間で色が濃いセルが集まっている場合、それらのカテゴリ間に強い関係があることがわかるね。
また、ヒートマップにはしばしばクラスタリングが適用されることがあるんだ。これによって、類似したパターンを持つカテゴリが近くにまとまるようになるんだ。クラスタリングされたヒートマップでは、カテゴリ間の関係だけでなく、カテゴリのグループ化も観察できるよ。
ニャー助: なるほどニャ!ヒートマップは色の濃淡で数値データを表現していて、カテゴリ間の関係やグループ化を観察できるんだニャ。
マチコ先生: そうだね、ニャー助。ヒートマップは、データの強度や密度を視覚的に表現できるから、非常に便利だよ。今後もさまざまな場面でヒートマップを活用してね。
ニャー助: ありがとうニャ、マチコ先生!ヒートマップを上手に使えるようになるニャ!とりあえず今回はこれくらいかにゃ?(疲れたニャ)
マチコ先生:いいえ、ニャー助。まだほかにビッグデータの可視化があるわね。
応用手法その3:ビッグデータの可視化
ニャー助:それってどうするの、マチコ先生?ビッグデータの可視化についても、疲れたけどいい機会だから同じように教えて欲しいニャ。
マチコ先生: もちろん、ニャー助(結構根性があるわね)。ビッグデータの可視化では、大量のデータを効果的に扱うための手法が必要だよ。ヒストグラムや散布図行列などの手法が使われることが多いけれど、今回は、ヘックスビンプロットについて説明するね。ヘックスビンプロットは、散布図のようにデータをプロットするけれど、密度の高い領域を六角形のビンで表現することで、ビッグデータを効果的に可視化できるよ。
ニャー助: なるほどニャ。じゃあ、Rのコードとフェイクデータで教えてニャ!
マチコ先生: いいね!フェイクデータとして、大量の点のx座標とy座標をランダムに生成してみようね。
# 必要なライブラリをインストール
install.packages("hexbin")
# ライブラリを読み込む
library(hexbin)
# フェイクデータを作成(大量の点のx座標とy座標)
set.seed(1)
x <- rnorm(10000)
y <- rnorm(10000)
# ヘックスビンプロットを作成
bin_data <- hexbin(x, y, xbins = 50)
plot(bin_data, main = "Hexbin Plot", colorcut = seq(0, 1, length = 10), colramp = function(x) {colorRampPalette(c("white", "red"))(x)})
ニャー助: おおお、ヘックスビンプロットで、大量のデータの密度が一目でわかるニャ。でもどうやって解釈したらいいにゃ?
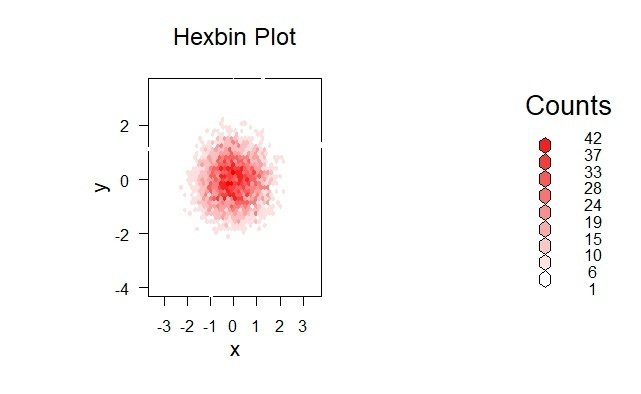
マチコ先生: ヘックスビンプロットは、散布図の一種で、2つの連続変数間の関係を表現するんだ。ただし、ヘックスビンプロットでは、点ではなく六角形の「ビン」を使ってデータを表現するよ。ヘックスビンプロットの解釈について説明するね。
ヘックスビンプロットでは、平面を六角形のビンで区切って、各ビンに含まれるデータポイントの数を色の濃淡で表現するんだ。色が濃いほど、そのビンに含まれるデータポイントの数が多いことを意味しているよ。逆に、色が薄いほど、そのビンに含まれるデータポイントの数が少ないことを示しているね。
ヘックスビンプロットを解釈する際には、まず色の濃淡がどのように分布しているかを観察することが大切だよ。色の濃いビンが集まっている場合、データがその領域に集中していることがわかるね。また、色の濃淡が特定のパターンを持っている場合、2つの変数間に関係があることが示されるよ。
ニャー助: なるほどニャ!ヘックスビンプロットは色の濃淡でデータの密度を表現していて、データの分布や変数間の関係を観察できるんだニャ。大量のデータポイントや重なりがある場合にも使えるんだニャ!
マチコ先生: そうだね、ニャー助。ヘックスビンプロットは、ビッグデータの密度を視覚的に表現できるから、非常に便利だよ。今後もさまざまな場面でビッグデータの可視化を活用してね。
ニャー助: ありがとうニャ、マチコ先生!ビッグデータの可視化も上手に使えるようになるニャ!これで、可視化がおわったら、データ分析も終わりかニャ?
可視化の限界ってなにニャ?
マチコ先生: いいえ、ニャー助、データの可視化はとても大切だけど、それだけでは十分じゃないこともあるんだ。データの可視化をしないと何が問題か、考えたことがある?
ニャー助: うーん、データの可視化をしないと、データの傾向やパターンがわかりにくいニャ?
マチコ先生: その通り!でも、データの可視化にも潜む問題があるんだ。例えば、グラフのスケールを変えるだけで、データの印象が大きく変わってしまうことがあるよ。だから、可視化だけではなく、統計的な分析手法も使ってデータを解釈することが大切なんだ。
ニャー助: なるほどニャ。でも、どうして可視化の先に分析手法を進める必要があるのニャ?
マチコ先生: 良い質問だね。データの可視化は、データの傾向やパターンを発見する第一歩だけど、実際にその傾向が偶然ではなく、本当に意味のあるものなのかを確かめるためには、統計的な分析が必要なんだ。例えば、相関関係や因果関係を明らかにするために、さまざまな分析手法を使ってデータをさらに詳しく調べることが大切だよ。
ニャー助: なるほどニャ。データの可視化だけではなく、分析手法も大切なんだニャ。これからもっと深くデータを理解するために、分析手法も学びたいニャ!
マチコ先生: そうだね、ニャー助。データの可視化と分析手法は、データ解析の両輪だから、どちらも大切にしてね。
ニャー助:わかったニャ!でも、今日はいろいろ学びすぎてもうだめ、疲れたニャー(ゴロゴロ)
終わりに
マチコ先生:おつかれ、ニャー助、今日はデータの可視化についてたくさん学んだね!これで、さまざまなデータを見やすく表示できるようになったんだから、すごい進歩だよ。
ニャー助: ありがとうニャ、マチコ先生!今回のレクチャーで、データの可視化の面白さがわかったニャ。これからも、さまざまなデータを可視化して、自分の研究や仕事に役立てたいニャ。
マチコ先生: そういう意欲があることが一番大切だね。これからも一緒に学んでいこうね!私もニャー助と一緒にいると、楽しくてほっこりするから、また次回も楽しみにしているよ。
ニャー助: うれしいニャ!次回もマチコ先生と一緒に学べるのを楽しみにしてるニャ。また、次回のレクチャーで会おうニャ!
マチコ先生: じゃあ、また次回ね。バイバイ!
ニャー助: バイバイニャ!
◆ツイッターでマチコ先生とニャー助が学ぶデータサイエンスの最新記事のお知らせをしています。
