
小学生でも分かる!Pythonプログラミング - 式を綺麗に並べる / .append( ) / len( ) / .format( ) / f-strings
← preview
next →
Program : 綺麗な10000×10000レベルの掛け算表を作る
今回は10000×10000のような大きい数の掛け算表を作る事を考えます。
実用性は完全に無視。
今回重要視するのは「綺麗に並べること」です。
失敗するのは分かりきっているので
range(1,10001)ではなく
range(1,101) に縮小してコードを書いていきます。
for i in range(1,101): # range(1,10)から変更
for j in range(1,101): # range(1,10)から変更
# 式を9つ書いたら改行
if j == 9:
print(f"{i}×{j} = {i*j}",end=" ")
print()
# 計算結果が1桁の場合
# 式の後の空白を1つ分多くする
elif i*j < 10:
print(f"{i}×{j} = {i*j}",end=" ")
else:
print(f"{i}×{j} = {i*j}",end=" ")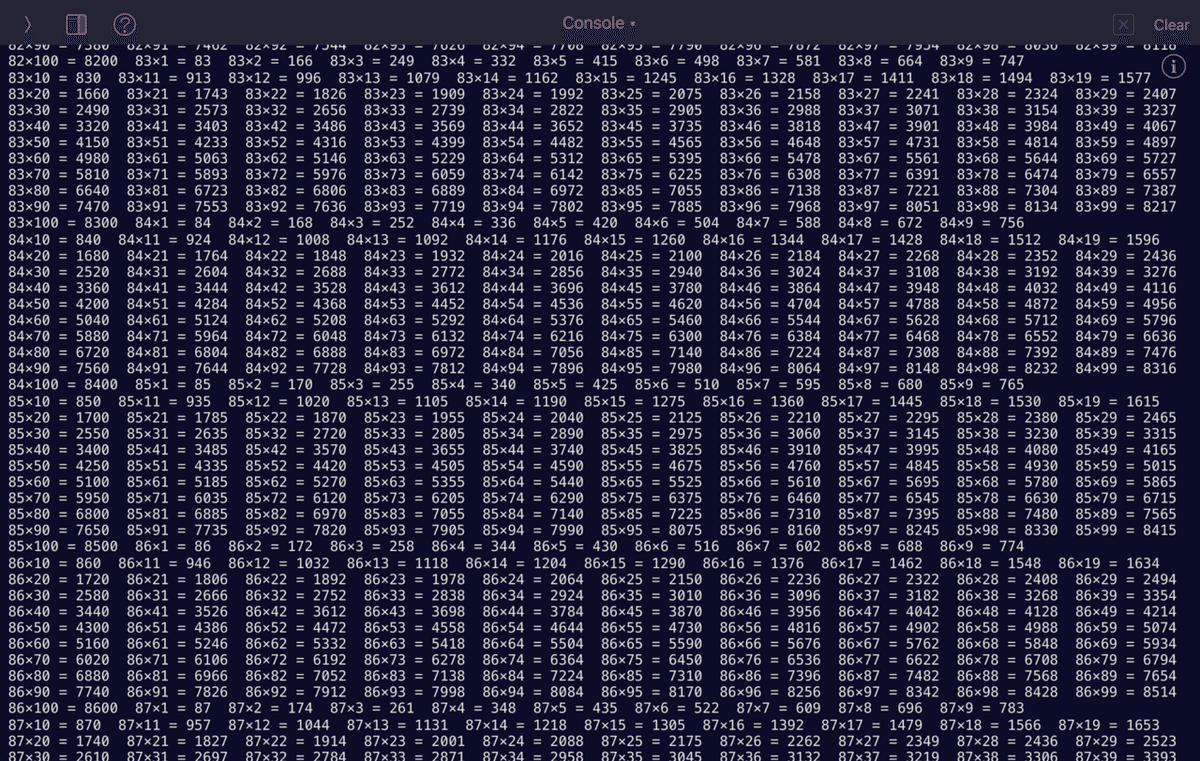
>> 改善すべき点
スクリプトや出力された一覧表を見て
「ココがイヤだ!」
と思うことを挙げてみましょう。
式と式の間隔が狭くて見づらい
どこからどこまでが
同じ「段」なのか分かりにくい各値の桁数が違うせいで、
行の長さにバラツキがあって見づらい最終的に
「10000 × 10000 =100000000」と
出力されるわけだが、カンマ( , )が無いと見づらい式を何回も書くのが面倒くさい
これらの点をなるべく短い記述で
解決したいですね。
>> 完成図をイメージする
改善点すべき点を受けて、
「こんな風にしたい」という
完成図をイメージしましょう。
式を100個書いたら、
2〜3行分のスペースを作ろう。9×9の時は1つの段が終わったら
改行させていた。
今回は、式を5個書いたら
改行されるようにしよう。これから表示されるのが、
何の段なのか分かるようにしよう。3桁毎にカンマ( , ) が入るようにしよう。
例 ) 1,234,567,890「 × 」と「 = 」は全て共通で使うので、
縦に綺麗に並ぶようにしよう。式と式の間隔が、
空白文字2,3個分になるようにしよう。長くて面倒な記述をもっと単純化しよう。
今回はこの目標を達成できるように頑張りましょう。
coding

やり方が分かっている項目から反映させていきましょう。
① 式を100個書いたら2〜3行分のスペースを作る
「 for i in range(1,101) 」の「 i 」に
「 1 」が代入された後、
「 for j in range(1,101) 」の「 j 」に
「1〜100」が順番に代入されます。
式を100個書いたら
2〜3行分のスペースを作るためには
「 j ( 掛ける数 )」が
「100」になった時に改行したらいいですね。
# もし、jが100と等しいなら:
# 式を書いて
# 3回改行
if j == 100:
print(f"{i} × {j} = {i*j}", end=" ")
print("\n"*2)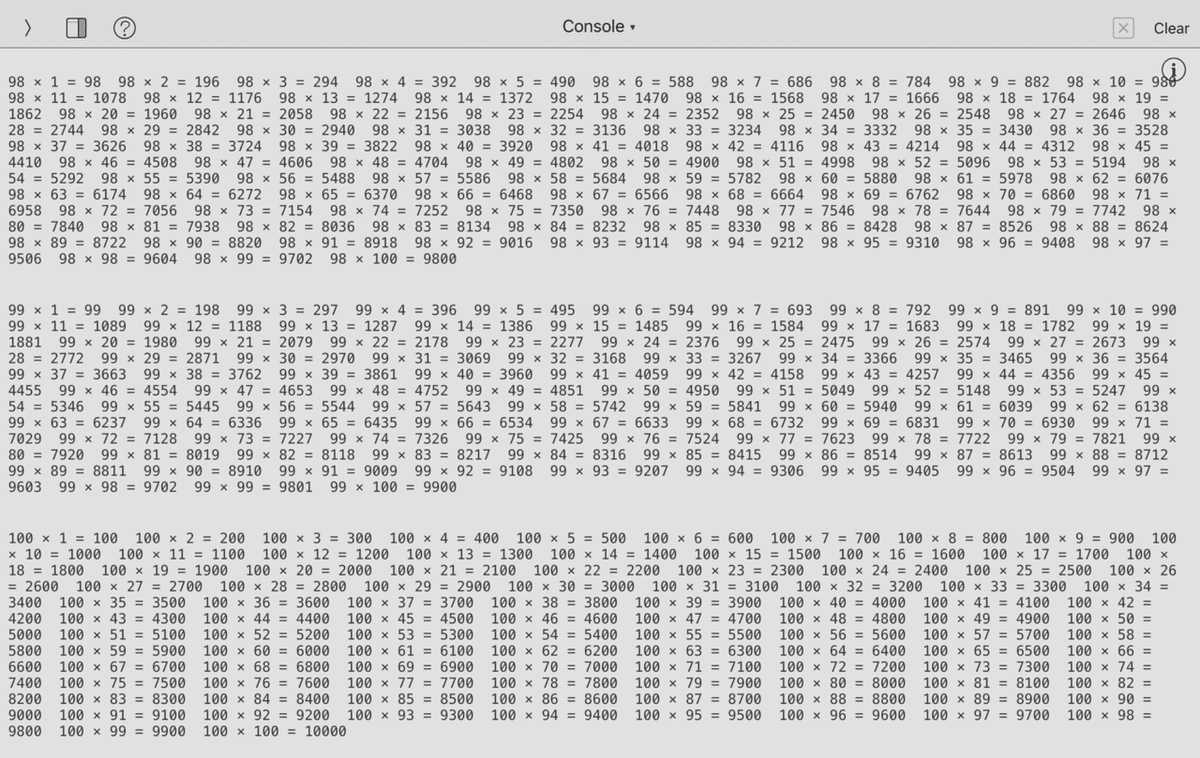
段がどこからどこまでか分かりやすくなった
② 式を5つ書いたら改行する
式を5つ書く毎に改行したい場合、
「 j ( 掛ける数 ) 」が
「 5の倍数 」の時に改行すればよいです。
「 5の倍数 」とは、言い換えれば
「 5で割った時、余りが0になる数 」です。
「 j % 5 ( jを5で割った時の余り) 」と
「 0 」が等しい場合に発動させればいいので、
「 elif j % 5 == 0: 」という書き方になります。

( j が5の倍数だったら )
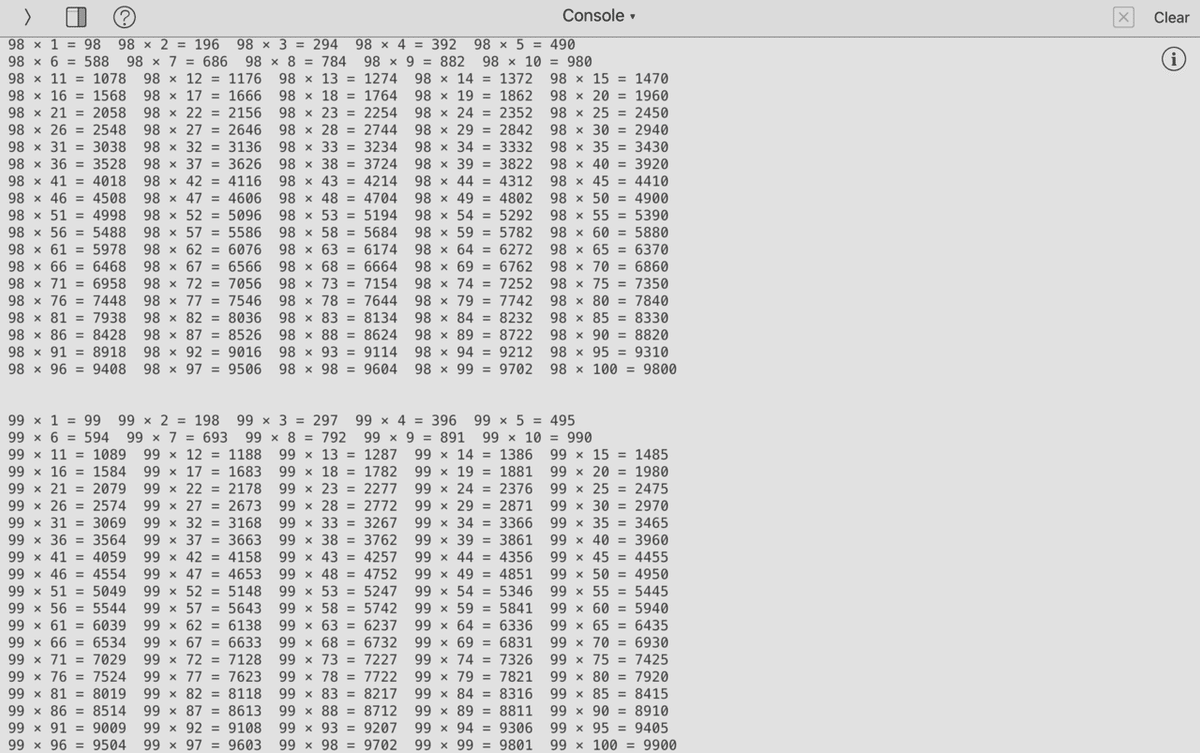
なったタイミングで改行されています。
これだけでも随分と見やすくなりました。
③ これから表示されるのが何の段なのか分かるようにしよう
「1の段」は「1×1」から始まり、
「2の段」は「2×1」から始まり、
「3の段」は「3×1」から始まり、
「4の段」は「4×1」から始まり、
「5の段」は「5×1」から始まります。
「これから○の段が始まりますよ」
という境界線を引くタイミングは、
「 j == 1: 」という条件文が
「 True ( 真 ) 」になる時ですね。
何の段なのかを示す境界線は
「 式を書き始める前 」を引きたいので、
式を出力する命令文よりも前に
命令文書いてやりましょう。

式より前に書く。
式を出力する条件文より先に書かないと
「else:」が先に発動して
1×1 = 1 ========= 1の段 ==========
1×2 = 2 1×3 = 3 1×4 = 4 1×5 = 5
👆こんな感じになってしまいます。
④ 様々な数値に対応できるように変数を用意する
今は「range(1,101)」と、
数値を固定して書いていますね。
しかし、rangeの値を変えてしまうと
他の箇所にも影響が出てしまいます。
その度に全ての値を
手作業で書き換えるのは大変面倒です。
書き直しを避けるためにも、
きちんと変数を用意してやりましょう。

「 f"=========== { i }の段 ============" 」
このような線を何個も書くのも面倒ですね。👆
これも変数を使ってまとめてしまいましょう。
# 変更前
print(f"========== {i}の段 =============\n")
# 変更後
line = "="*30
print( f"{line} {i}の段 {line}\n")
# 👇こう書いてもOK。ただし一括で調整はできない。
print(f"{'='*30} {i}の段 {'='*30})
また、条件分岐する度に
print( f"{ i } × { j } = { i*j }" , end=" " )
いちいちこの式を書かなければいけないのが
アホほど面倒なので、これもひとまとめにします。
※「end」はオプション引数なので逐一書きます。
calc = f"{i} × {j} = {i*j}"
print(calc, end=" ")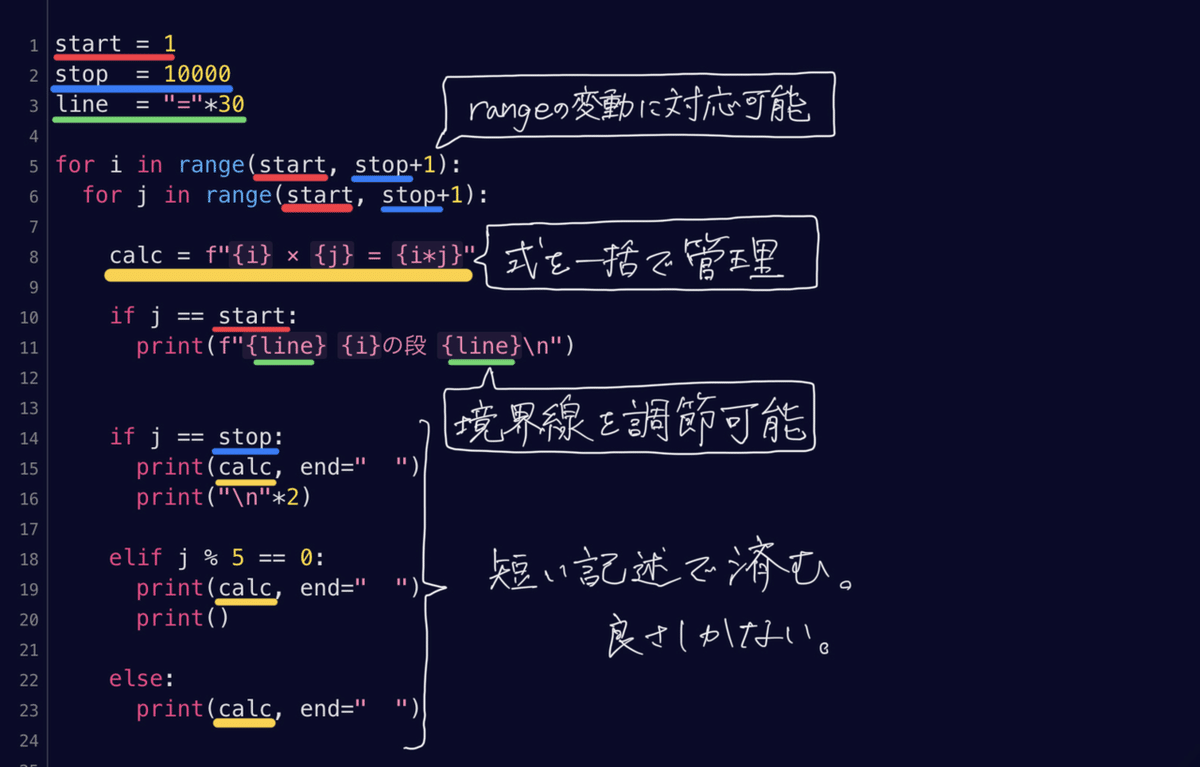
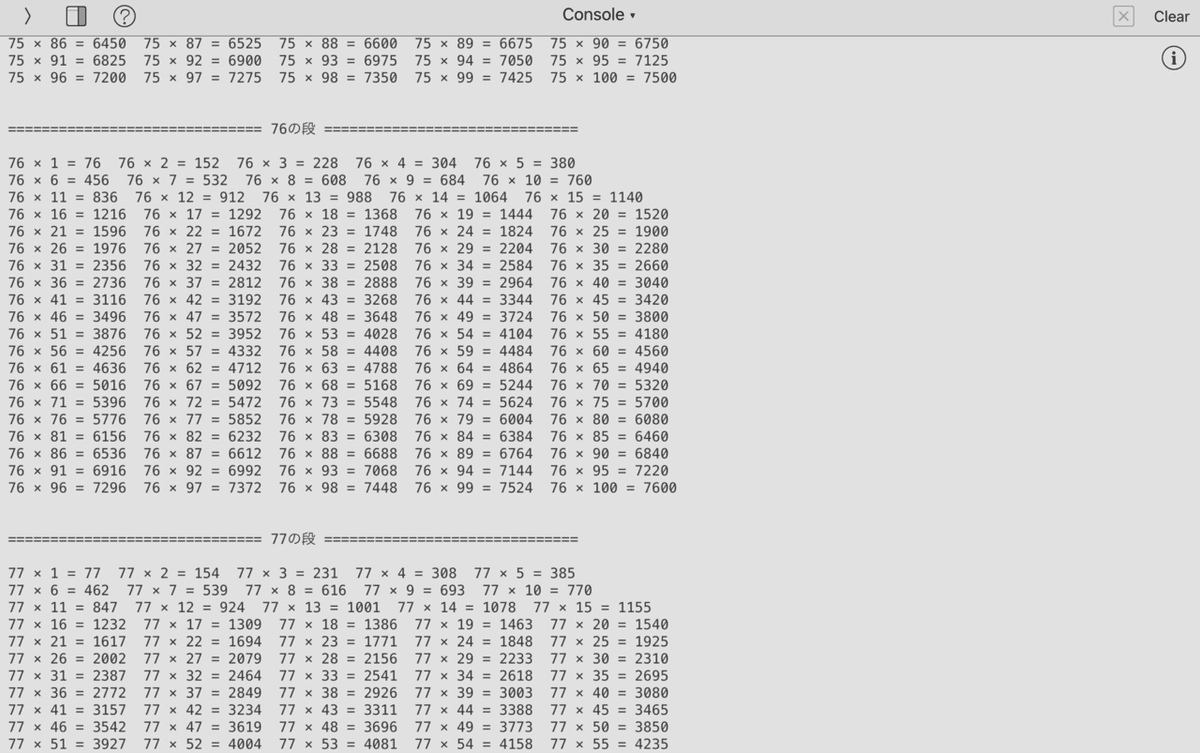
対応できるようになりました。
⑤ + ⑥「×」や「=」の位置を揃える / 式と式の間隔が必ず空白文字2つ分になるようにする
これが今回の最大の関門でしょう。
こちらのコードを実行してみます。
# Python
start = 1
stop = 10000
line = "="*30
for i in range(start,stop+1):
for j in range(start,stop+1):
calc = f"{i} × {j} = {i*j}"
if j == start:
print(f"{line} {i}の段 {line}\n")
if j == stop:
print(calc, end=" ")
print("\n"*2)
elif j % 5 == 0:
print(calc, end=" ")
print()
else:
print(calc, end=" ")
10000×10000はさすがに時間がかかるので
ちょうどいいところで中断しましょう。
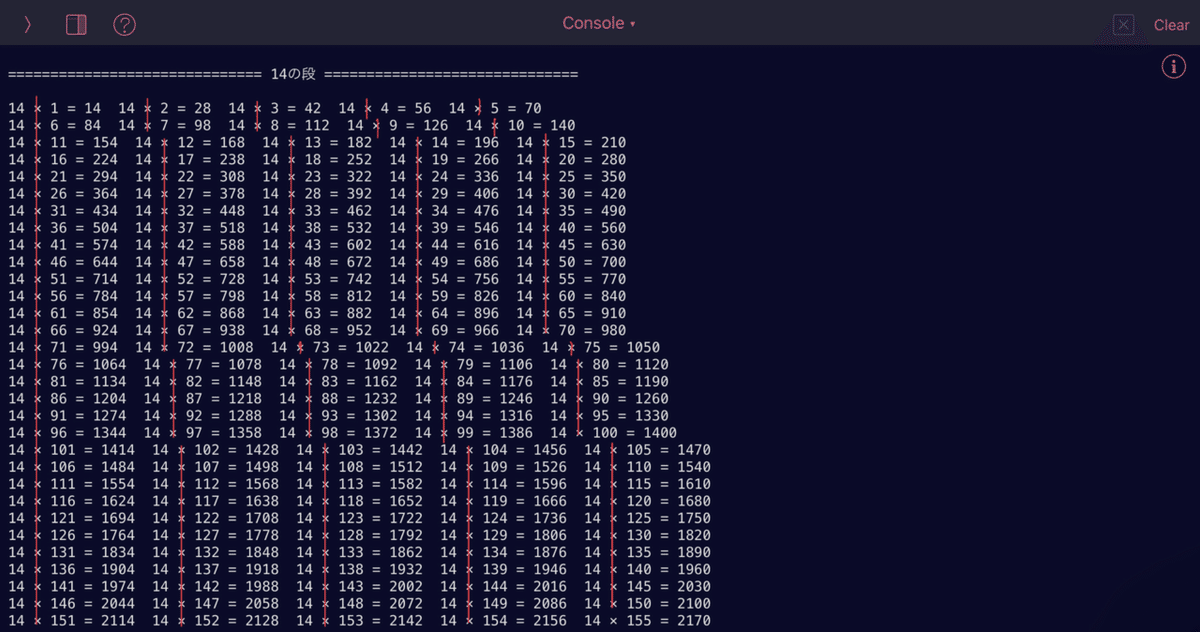
例えば「 range(1,101) 」だったとしても
1 × 1 = 1[ ]
100 × 100 = 10000
最小の式の長さと最大の式の長さに
大きな差があります。
この長さの違いがズレの原因に
なっているわけですね。
100×100の場合、
掛ける数 : 1〜3桁
掛けられる数 : 1〜3桁
積 : 1〜5桁
このように各値の桁数が変動してしまいます。
これが 10000×10000、
もしくはそれ以上になったら、
「一体何個の条件分岐を
作らなきゃいけないんだろう?」と思いませんか?
append

>> appendメソッド
>> append ( アペンド )
= 追加。
ここで、新しいメソッドをご紹介します。
「 appendメソッド 」です。
これは list型オブジェクト用 のメソッド。
⚠️ tupleやdictなどに対して使う事はできません。
append(追加)メソッドは名前の通り、
「 リストに値を追加するためのメソッド 」です。
使い方は以下の通りです。
値を追加する用の [ 空リスト ] を用意
( [ 既に値が入っているリスト ] でも使える )値を追加したいリスト名.append( 追加する値 ) の形で記述
print( リスト名 ) で確認

含まれているかどうかを判定して仕分け
len

>> len関数(メソッド)
>> length ( レングス )
= 長さ、全長、丈。
次に紹介するのは「 len関数 」です。
この len関数 は
引数の文字数を返してくれる関数です。
文字数をカウントするためには、
値を1つ1つに切り分けることができる
オブジェクトである必要があります。
つまりlen関数の引数は
[ iterable_object ] でなくてはならないわけです。
そのため、
int型,float型,bool型オブジェクトなどは
str型に変換する必要があります。
僕はよく、うっかり
a = 10**1000
print( len(a) )
👆このように書いてエラーを起こしてしまいます。
今後もやってしまうと思います。
int型は [ iterable ] ではありません。
print( len( str(a) ) )
ちゃんと忘れずにstr関数を使って
[ iterable ] にしてあげましょう。
以上、新しい関数/メソッドの紹介でした。
re:coding
⑦ appendメソッド + len関数 で各値の桁数の組み合わせを弾き出す
100×100までの計算をすると、
● 1桁 × 1桁 の最小最大
最小 : 1×1 = 1 ( 1桁 × 1桁 = 1桁 )
最大 : 9×9 = 81 ( 1桁 × 1桁 = 2桁 )
● 1桁 × 2桁 または 2桁 × 1桁 の最小最大
最小 : 1×10 = 10 ( 1桁 × 2桁 = 2桁 )
最大 : 9×99 = 891 ( 1桁 × 2桁 = 3桁 )
最小 : 10×1 = 10 ( 2桁 × 1桁 = 2桁 )
最大 : 99×9 = 891 ( 2桁 × 1桁 = 3桁 )
......(省略)
● 3桁 × 3桁 ( 上限 )
上限 : 100×100 = 10000 ( 3桁 × 3桁 = 5桁 )
こんな感じで色々な組合わせが考えられます。
組み合わせが複数あるということは、
それだけズレが起こるリスクがあるという事です。
しかし、
色々な組み合わせが考えられるとは言え
if len(str( i ))==1 and len(str( j ))==1 and len(str( i*j ))==1:
......
elif len(str( i ))==1 and len(str( j ))==1 and len(str( i*j ))==2:
......
elif len(str( i ))==1 and len(str( j ))==2 and len(str( i*j ))==2:
......
elif ............
......こんな風に、組み合わせの数だけ
条件分岐させるなんて馬鹿馬鹿しいですよね。
どうしたらいいでしょうか?
例えば、こんなリストを作ることを考えて下さい。
[ 掛けられる数の桁数 , 掛ける数の桁数 , 積の桁数 ]
ちょっと長いので、
以下のように変数に置き換えたいと思います。
[ a, b, x ]
start = 1
stop = 100
for i in range(start,stop+1):
for j in range(start,stop+1):
a = len(str(i))
b = len(str(j))
x = len(str(i*j))
list_abx = [a,b,x] # 👈これね例)
2 × 3 = 6 → [ 1, 1, 1 ]
12 × 3 = 36 → [ 2, 1, 2 ]
123 × 45 = 5535 → [ 3, 2, 4 ]
1234 × 5678 = 7006652 → [ 4, 4, 7 ]
もし、100×100全ての [ a, b, x ] を出力したら
こんな内容になってしまいます。
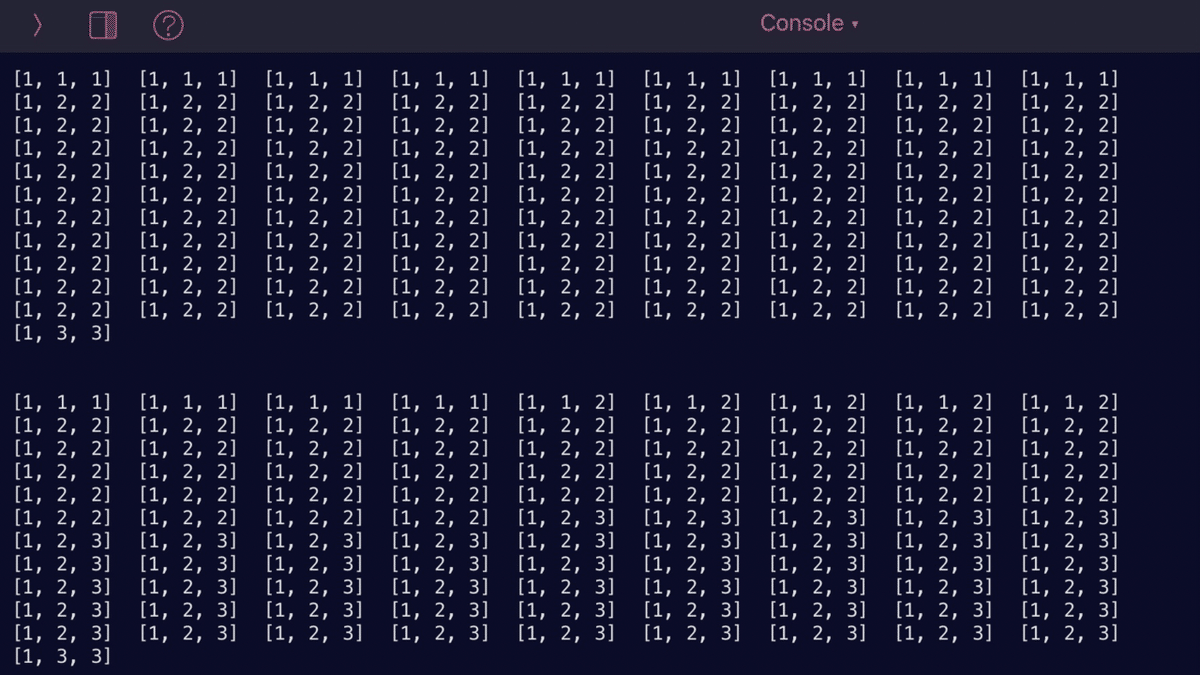
[ a, b, x ]リストの内容がカブっているのなら
出力しないで欲しい。
そこで、if文とappendメソッドを駆使して
「 追加用のリストの中に、同じ値が無ければ
その [a, b, x]リスト を追加する 」
という命令をしてやることにしましょう。
list_ABX = []
if list_abx not in list_ABX:
list_ABX.append(list_abx)
# Python
start = 1
stop = 100
list_ABX = []
for i in range(start,stop+1):
for j in range(start,stop+1):
a = len(str(i))
b = len(str(j))
x = len(str(i*j))
list_abx = [a,b,x]
if list_abx not in list_ABX:
list_ABX.append(list_abx)
for data in list_ABX:
print(data)
print(f"{len(list_ABX)}通りの組み合わせ")
⑧ 空白文字数の法則性を調べる
出力された組み合わせを元にこんな図を作ってみました。

>> blank ( ブランク )
= 空白。〔略〕bl
※ 「 brank = 口枷(くちかせ) 」ではないので注意。
ちなみに、HTML/CSSの <br/> は break(強制改行)
各値の桁数は変動するけれど、
「 i 」 「 j 」「 i*j 」の桁数( a, b, x )に合わせて
空白文字の数( bl )も変われば、
横位置を合わせる事ができる
という事がわかります。
しかも、空白文字( bl )をいくつ入力すればいいのかは
空白の数( bl ) =
各値の桁数の上限( max ) - 取り出した値の桁数 ( a, b, x )
という、
超簡単な引き算で弾き出せる事が
この図から分かります。
⑨ コードに反映させる
さらにここから、もう一工夫です。
今は range( start, stop ) が
掛けられる数と掛ける数で同じ範囲になっていますが、
for i in range(1,11):
for j in range(1,10001):
こんな風に別の範囲になっても対応できるように
変数を増やしましょう。
start_a, stop_a = 1,100
start_b, stop_b = 1,100
また、今は100×100=10000までの想定なので
桁数の上限が [ 3桁, 3桁, 5桁 ] になっていますが、
10000×10000=100000000 ( [5,5,9] )等にも
対応できるように
上限を変数に置き換えてしまいましょう。
max_a = len( str( stop_a ) )
max_b = len( str( stop_b ) )
max_x = len( str( stop_a * stop_b ) )
range を変更すると、
連動して桁数上限も変わるわけです。
これらの点を踏まえて修正すると

桁数の上限 = stopに入力された数の桁数
start_a, stop_a = 9990,10000
start_b, stop_b = 1,10000
max_a = len(str(stop_a))
max_b = len(str(stop_b))
max_x = len(str(stop_a * stop_b))
line = "="*30
for i in range(start_a, stop_a+1):
for j in range(start_b, stop_b+1):
a = len(str(i))
b = len(str(j))
x = len(str(i*j))
bl_a = max_a - a
bl_b = max_b - b
bl_x = max_x - x
calc = f"{' '*bl_a}{i} × {j}{' '*bl_b} = {i*j}{' '*bl_x}"
if j == start_b:
print(f"{line} {i}の段 {line}\n")
if j == stop_b:
print(calc, end=" ")
print("\n"*2)
elif j % 5 == 0:
print(calc, end=" ")
print()
else:
print(calc, end=" ")
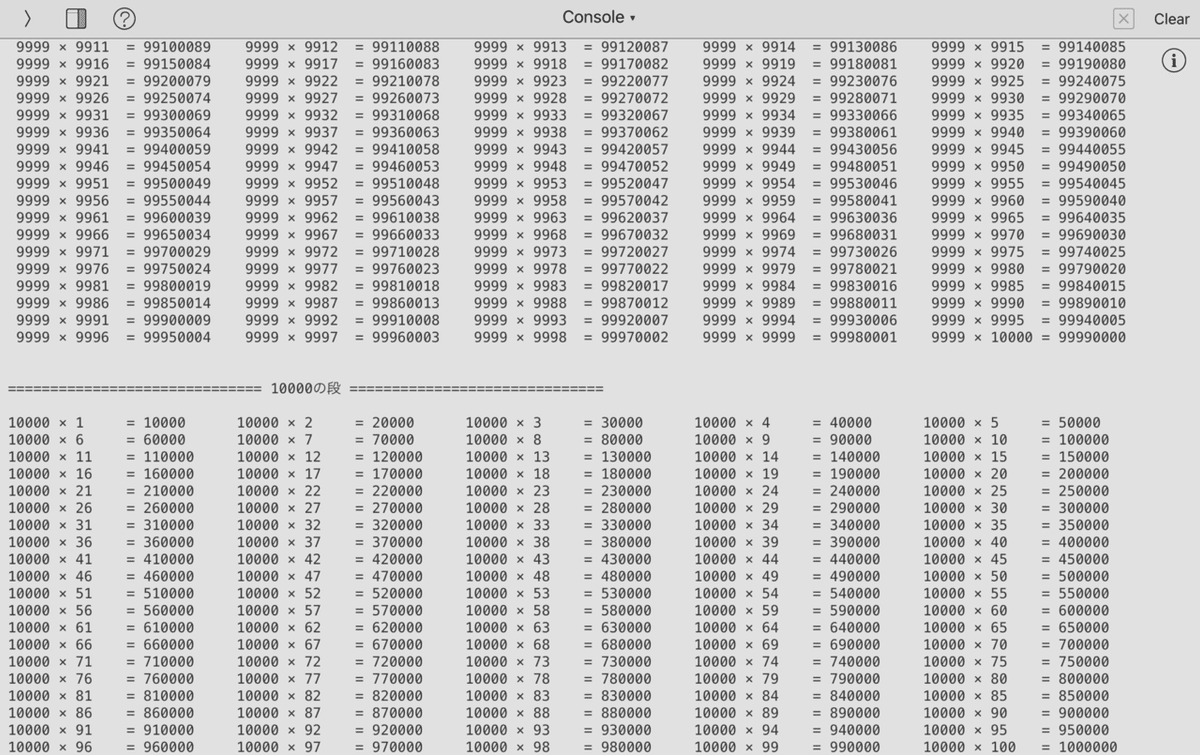
⑩ 数字にカンマを入れる(formatメソッド)
数字に自動的にカンマを入れる方法ですが、
そこまで難しくはありません。
n = 1234567
print("{:,}".format(n))
# >>> 1,234,567このように 「 "{ : , }".format( n ) 」と書いてやるだけです。
でも、fotmatメソッドでは
{波括弧}の中に空白文字すら書いてはいけないはず...。
と思いませんでしたか?
「 : , 」 ← これは引数ではなく
「カンマ付き」という「書式設定(フォーマット)」です。
だから指示記号として{波括弧}内に書くのです。
f-stringsの場合はこのようにします。
n = 1234567
print(f"{n:,}")
# >>> 1,234,567
では、実際のコードにも反映させてみましょう。
calc = f"{' '*bl_a}{i} × {j}{' '*bl_b} = {i*j}{' '*bl_x}"
# 👇変更
calc = f"{' '*bl_a}{i:,} × {j:,}{' '*bl_b} = {i*j:,}{' '*bl_x}"これでカンマを付けることに成功したのですが...
カンマ( , )を付けて実行すると
とある問題が起こる事が分かります。
それは、式が長くなって「ズレる」って事です。
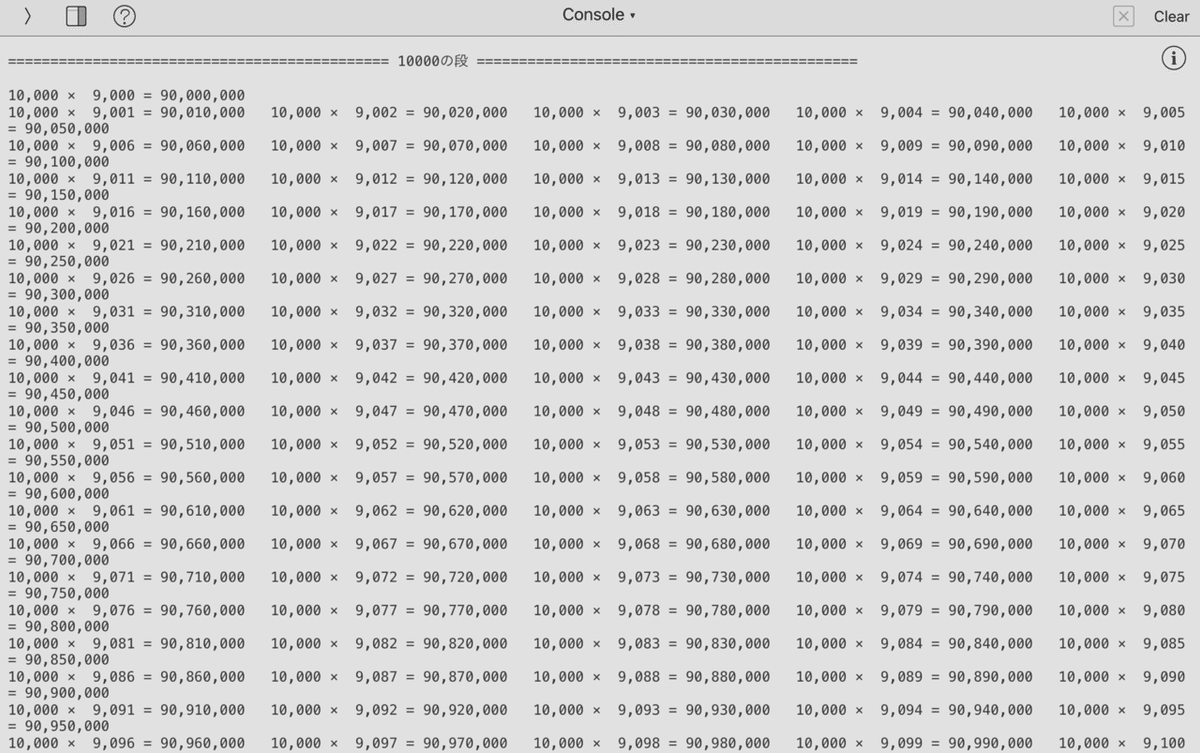
式が5つだと多いから3つで改行に変更しました。
しかし...
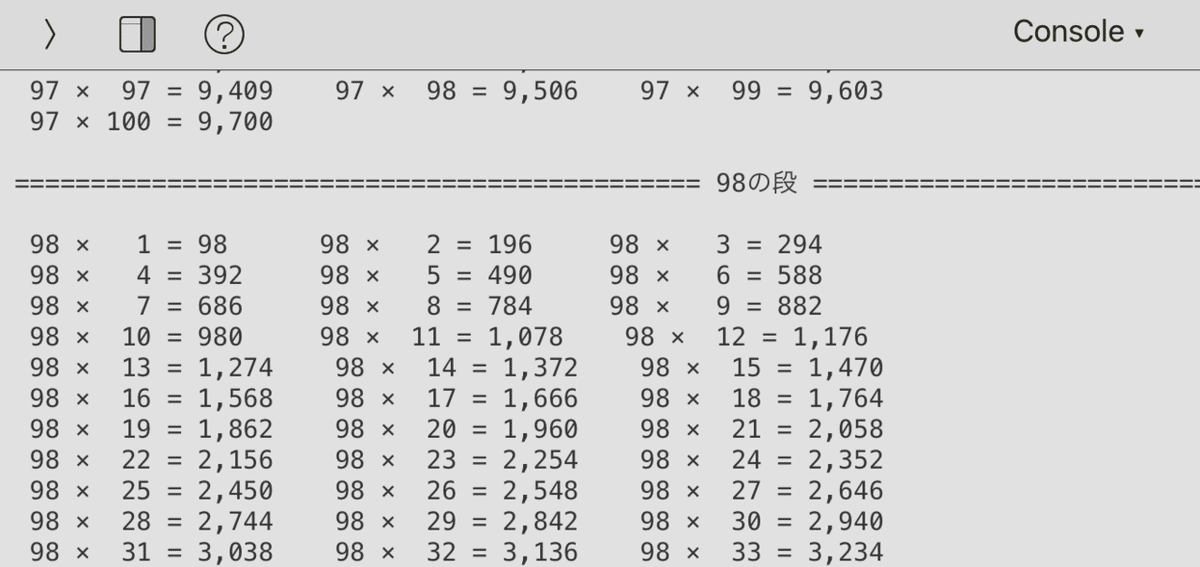
現状では「各値の桁数」だけを数えているので
カンマの付かない式が出てきた時にズレてしまうのです。
つまり「各値の桁数 + カンマの数」を
数える必要がある。
formatメソッド( f-strings )を使うことで
カンマを付加できるわけなので、
formatメソッドやf-stringsを使った状態の
文字数を数えてもらえればいいわけですね。

カンマなしのものを数えている
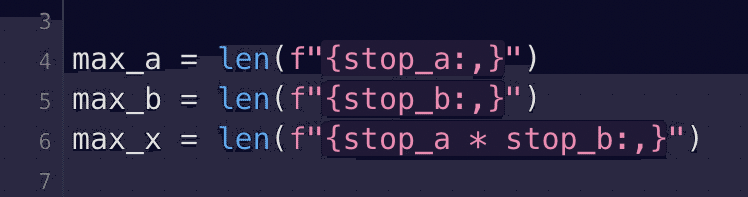
カンマありのものを数えてもらう
⑪ 最終調整
# 掛けられる数と掛ける数の範囲
start_a, stop_a = 900,1020 # 掛けられる数
start_b, stop_b = 99999900,100000000 # 掛ける数
# 各値の文字数上限
max_a = len(f"{stop_a:,}") # 掛けられる数
max_b = len(f"{stop_b:,}") # 掛ける数
max_x = len(f"{stop_a * stop_b:,}") # 積
# 境界線, 境界線2
line, line2 = "="*45, "-"*40
for i in range(start_a, stop_a+1): # 掛けられる数
for j in range(start_b, stop_b+1): # 掛ける数
# 各値にカンマをつけた文字列(str)
a = f"{i:,}" # 掛けられる数
b = f"{j:,}" # 掛ける数
x = f"{i*j:,}" # 積
# 各値にカンマを付けた時の文字数(int)
len_a = len(a) # 掛けられる数
len_b = len(b) # 掛ける数
len_x = len(x) # 積
# 空白文字数 = 桁数上限 - 使われた桁数(int)
bl_a = max_a - len_a # 掛けられる数
bl_b = max_b - len_b # 掛ける数
bl_x = max_x - len_x # 積
# 空白文字とカンマ付きの式
calc = f"{' '*bl_a}{a} × {' '*bl_b}{b} = {x}{' '*bl_x}"
# 取り出した掛ける数が、start_bと等しかったら
# 境界線を引いて、1回
if j == start_b:
print(f"{line} {a}の段 {line}")
print()
# 取り出した掛ける数が100の倍数の時
# 2回改行して、境界線2を引いて、1回改行
elif j % 100 == 0:
print("\n")
print(f"{line2} {a} × {b} 〜 {line2}")
print()
# 積の文字数が14文字以下 & 掛ける数が 3 の倍数の時
# 式を書いて、1回改行
if len_x <= 14 and j % 3 == 0:
print(calc,end=" ")
print()
# 積の文字数が14文字より多い & 掛ける数が 2 の倍数の時
# 式を書いて、1回改行
elif len_x > 14 and j % 2 == 0:
print(calc,end=" ")
print()
# それ以外の時
# 式を書く(改行なし)
else:
print(calc,end=" ")
# 取り出した掛ける数が stop_b と等しかったら
# 2回改行
if j == stop_b:
print("\n")
# 積が64bitを超えていたら
# エラーメッセージを出して、繰り返し処理中断
if i*j > 1<<64-1:
print("\n⚠️Calculation result exceeds 64-bit.\n\n")
break10000よりも大きな数の掛け算をしても大丈夫なように
とある桁数(14桁)を超えたら1行に表示する式の数を
3つから2つに減らすようにしました。
また、より目的の式を見つけ出しやすくするために
100個式を書いたら境界線を挟むようにしました。
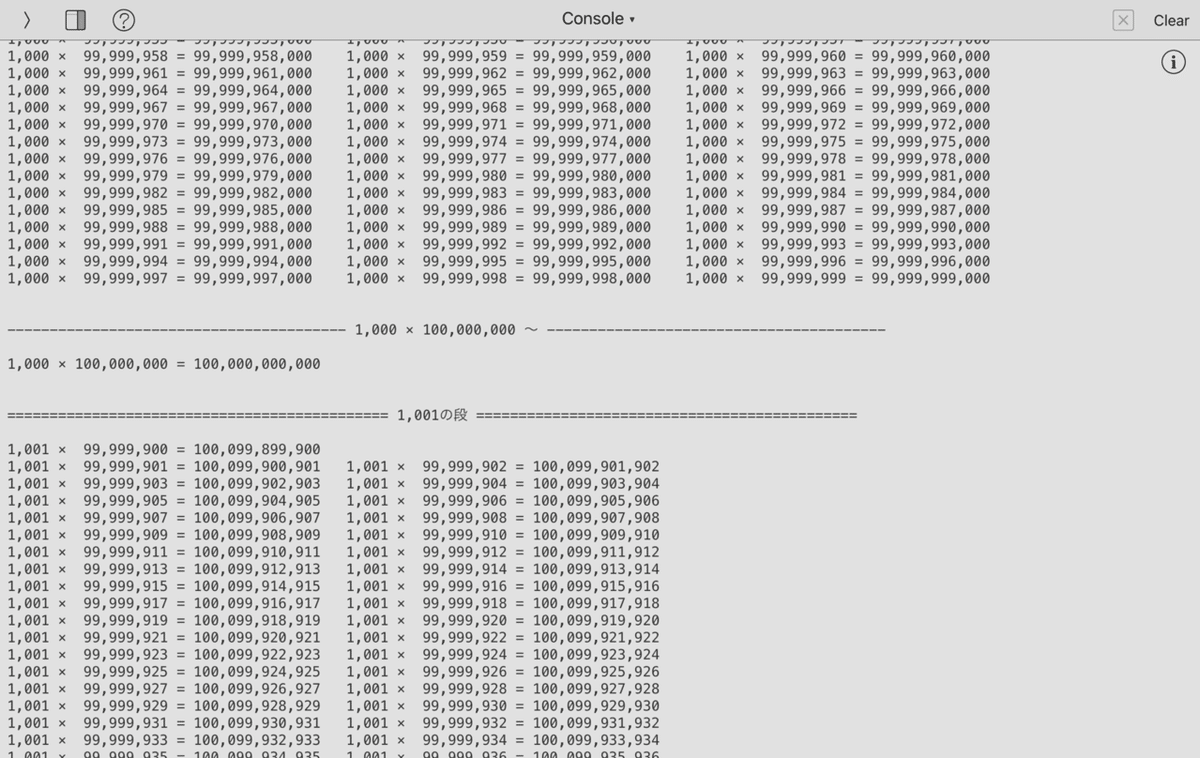
計算結果が64bitを超えた時にエラーが出て
処理を中断するようにしました。
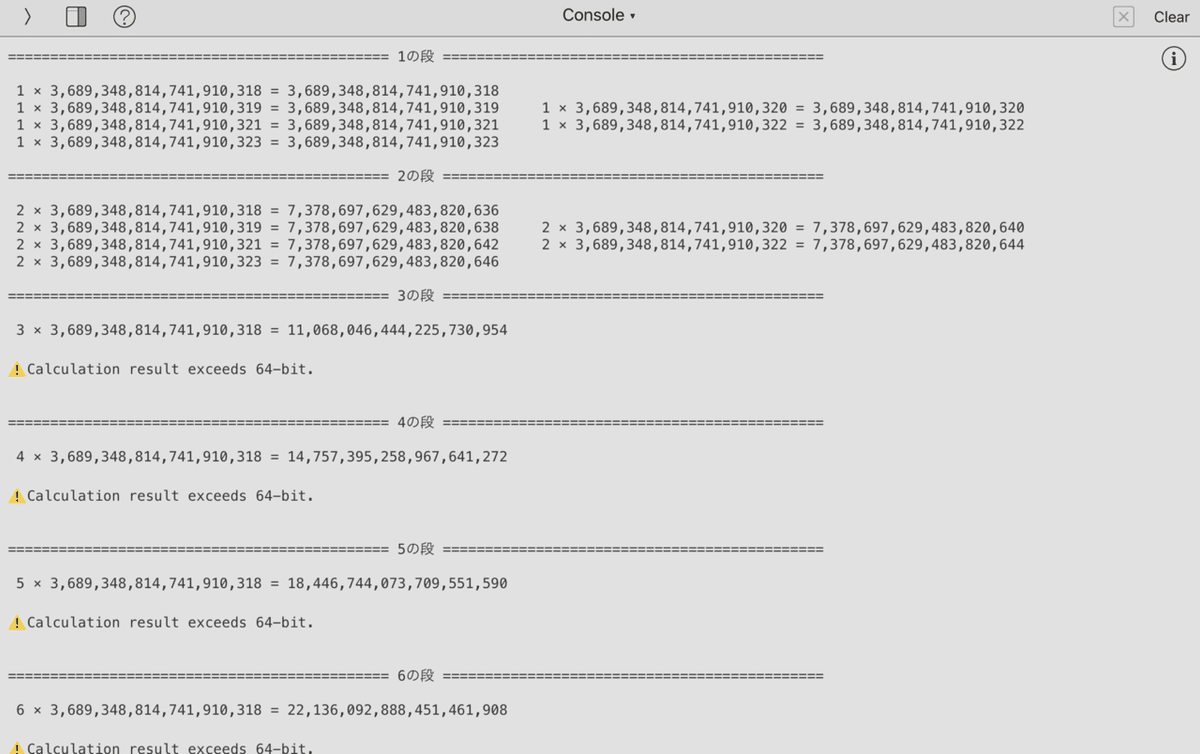
小さい数の掛け算では、このように表示されます。

もし気に入らない場合は、
条件分岐をさらに追加してあげましょう。
次の記事へ。
