
3次関数でチョロQみたいなイージング
noteを毎日書く2021年12月にしたいなと思う22日目!とある講義を行なったのでそのことについて書こうと思います。
はじめに
この講義は、主に小学生相手に行いました。従って、大半の大人の方も数学に気後れする必要ないはずです。道具として数学がどのように使われるのかを知っていただけることでしょう。
小学生だって知りたい
小学生に相手に関数、しかも3次関数です。もちろん本格的に何か数学の問題を解いたわけではありません。プログラミングの中で必要になったから数学を道具として使いました。
私は長年、数学や理科を子どもたちに指導してきましたが、はっきり言います。「分かりやすくは」理解しようとした結果です。何よりも先に「理解したい」という気持ちがなければ始まりません。
知りたいに応える、本質を見抜く
また、その手段として難解な言葉や現象、法則も本質を伝えることが肝心です。本質を見つける作業は余分な情報をいかにそぎ落とすかという作業になります。
3次関数を小学生に問うた些細な事例ですが、何かの参考になれば幸いです。
プログラミングで3次関数
具体的には「イージング」を扱う講座でした。イージングとは次のような動きのことで、英語でEase(イーズ:心地よい)が由来である言葉です。

言葉選びが大事
まずは講義の中で使う言葉を噛み砕きます。妥協はしません。使う言葉はブレないようにするし、その使う言葉1つ1つに拘ります。例えば、滑らかな動き→スムースな動きのように、子どもがイメージしやすいことに拘ります。
では関数はどうなのでしょう。まずは国語辞典を参照するところからです。
ある数yが他の数xの変化にしたがって変化するとき、xに対するyの呼び名
うーん厳しい。辞書引いたのに結構難しいですね。しかし、短く端的に表現できていることは一旦信じましょう。結果、次のように紹介しました。
何か数をつかって計算した結果の数がゲットできるね。このゲットできる仕組み、今日ならこの式のことを関数というよ。
イージング関数
イージング関数は、動き方の関数です。今回だと$${2.70158t^3-1.70158t^2}$$でした。この関数には秘密があります。
$${t = 0}$$のとき、0です
$${t = 1}$$のとき、2.70158 - 1.70158 = 1です
グラフは次のようになりますが、そんなに難しい話ではありません。$${t}$$が0のき0で、$${t}$$が1のときは1です。
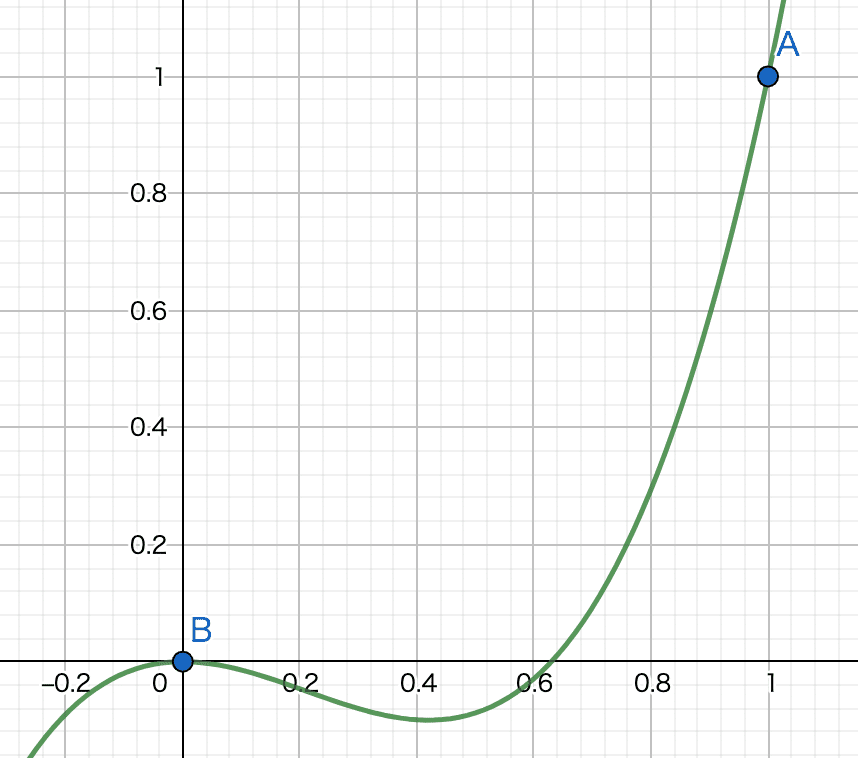
じゃあその間の値は?という話で、0.1とかだと$${t^3}$$は0.001とかなり小さくなって、$${t^2}$$は0.01と10倍大きいので、引き算するとマイナスになります。これが、チョロQのバックの仕組みになりますね。
やがて引き算の±は逆転します。そう1に向かうのですね。
イージングの仕組み
0〜1の数というのは何かと便利です。100%が1であるため、0〜1の連続した変化は%(パーセントのようなもの)と考えるといいでしょう。
$${目標 \times tの式}$$
とすることで、$${t}$$の式で表されたイージング関数($${tの式}$$)は目標達成度合い(パーセント)のような値だと捉えればいいのです。400動くことが目標であれば、
$${400 \times tの式}$$
といった具合です。
おわりに
いかがでしたか?式が動きを表す、そして関数という仕組みが少しは身近に感じられたのではないでしょうか?バイバイ!

(サンプルコード)
let t = 0;
let x1, y1, x2, y2;
function setup() {
createCanvas(900, 400);
background(100);
x1 = 200;
y1 = 0;
x2 = width;
y2 = height;
t = 0;
}
function draw() {
const x = lerp(x1, x2, tt(t));
const y = lerp(y1, y2, tt(t));
clear();
circle(x, 200, 50);
if(mouseIsPressed){
t += 0.008;
}
if(x > width + 100){
t = 0;
}
}
function tt(t){
return 2.70158 * t * t* t - 1.70158 * t * t;
}この記事が気に入ったらサポートをしてみませんか?
