
【Python】電磁波の屈折と反射(スネルの法則)
一様な媒質中を伝搬してきた電磁波は、異なる媒質の境界面に差し掛かると、透過波と反射波とに分けられるね。今回はマクスウェル方程式から境界面における境界条件を導出して、入射波、反射波、透過波の関係を表す境界条件の導出と、そこから透過係数、反射係数も導出するよ。
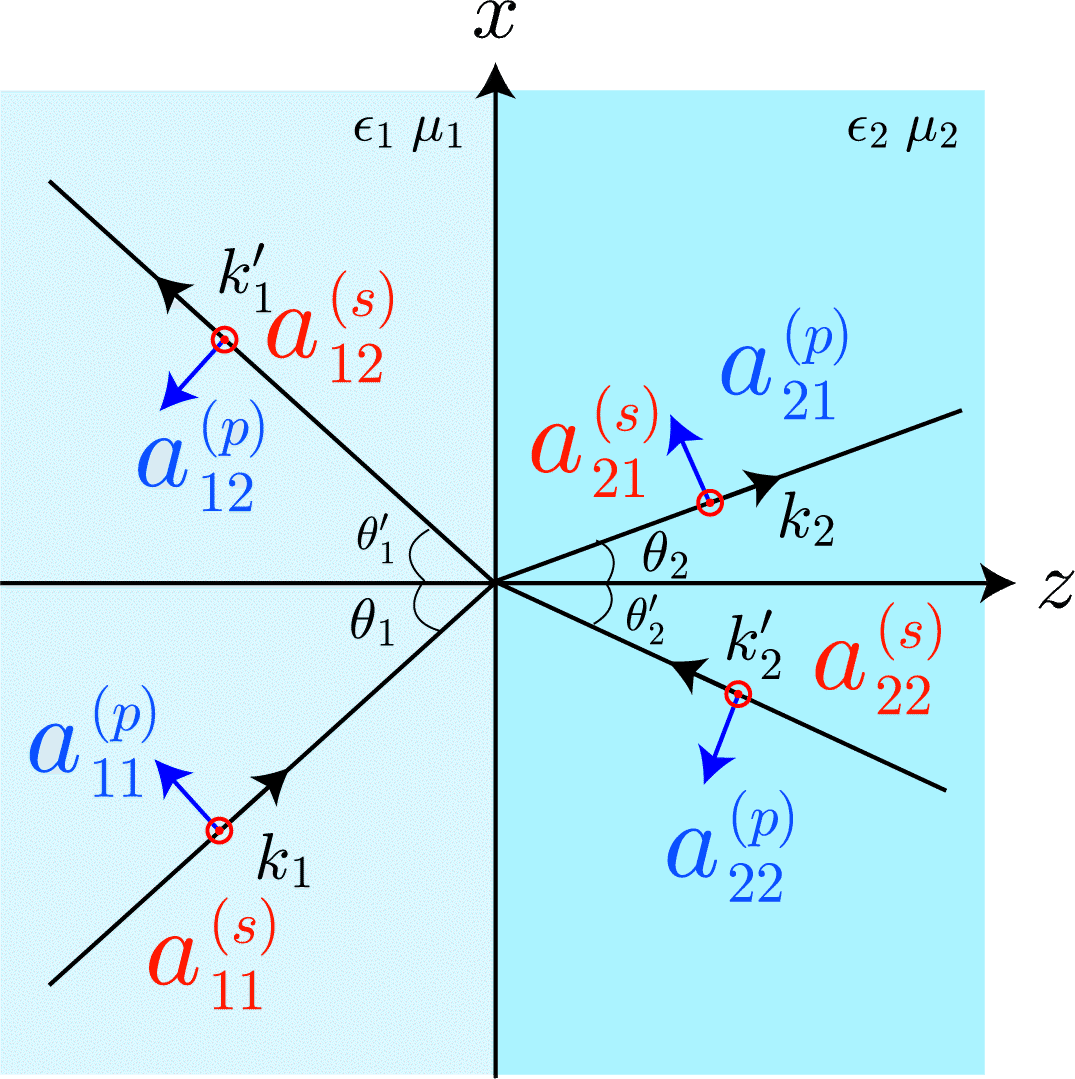
図:媒質1,2の誘電率と透磁率はぞれぞれ$${\epsilon_1, \epsilon_2}$$と$${\mu_1, \mu_2}$$とする。また、$${(s)}$$はS偏光、$${(p)}$$偏光を表す。誘電率$${\epsilon_1}$$と透磁率$${\mu_1}$$の媒質1と、誘電率$${\epsilon_2}$$と透磁率$${\mu_2}$$の媒質2の境界面における電磁波が満たすべき条件を導出するよ。各媒質内での電磁波はフーリエ変換後のマクスウェル方程式
$$
\boldsymbol{E}(\boldsymbol{r},\omega) = -i\omega\boldsymbol{A}(\boldsymbol{r},\omega)
$$
$$
\boldsymbol{B}(\boldsymbol{r},\omega) = \nabla \times \boldsymbol{A}(\boldsymbol{r},\omega)
$$
$$
\nabla^2 \boldsymbol{A}(\boldsymbol{r},\omega) + \frac{\omega^2}{v^2(\omega)}\boldsymbol{A}(\boldsymbol{r},\omega)= 0
$$
を満たすね。ただし、
$$
v(\omega) = \frac{c}{\sqrt{\epsilon(\omega)\mu(\omega)}}= \frac{c}{n(\omega)}
$$
だよ。$${n(\omega)}$$は屈折率って呼ばれるね。$${\omega}$$と$${v(\omega)}$$の関係は波数$${k}$$を用いて
$$
\omega = v(\omega) k=\frac{ck}{n(\omega)}
$$
となるのだけれども、媒質中の電磁波の$${\omega}$$は屈折率の大きさによらないので、媒質中では波数が$${n}$$倍となるね。つまり、真空中の波数と波長を$${k_0, \lambda_0}$$とすると、媒質中では$${k = nk_0}$$となり、波長は$${\lambda = \lambda_0 / n}$$となるね。
前にも述べだけれども電磁波は進行方向に対して、直角の方向に電磁波の振幅を持つね。電磁波の境界面付近での振舞いは、電磁波の境界面と並行な成分とその他の成分では異なるため、分けて考える必要があるよ。一般に境界面と並行な成分は$${s}$$偏光と呼ばれ、一方、残りの成分は$${p}$$偏光と呼ばれるよ。図示したとおり、各媒質における電磁波を区別するために添字を多用するね。媒質1中の進行波($${z}$$軸方向に進行する波)の波数ベクトル$${\boldsymbol{k}_1}$$、後進波($${-z}$$軸方向に進行する波)の波数ベクトル$${\boldsymbol{k}_1'}$$を
$$
\boldsymbol{k}_1 = k_1 (\sin\theta_1, 0, \cos\theta_1)
$$
$$
\boldsymbol{k}_1' = k_1' (\sin\theta_1', 0, -\cos\theta_1')
$$
と表した場合、媒質1の進行波$${\boldsymbol{A}_{11}}$$と後進波$${\boldsymbol{A}_{12}}$$は各偏光の振幅を用いて、
$$
\boldsymbol A_{11}=\left(\begin{matrix} a_{11}^{(p)} \cos\theta_1 \cr a_{11}^{(s)} \cr -a_{11}^{(p)} \sin\theta_1 \end{matrix} \right) e^{i \boldsymbol{k}_1 \cdot \boldsymbol{r}-i\omega_1 t}
$$
$$
\boldsymbol A_{12}=\left(\begin{matrix} -a_{12}^{(p)} \cos\theta_1' \cr a_{12}^{(s)} \cr -a_{12}^{(p)} \sin\theta_1' \end{matrix}\right) e^{i \boldsymbol{k}_1' \cdot \boldsymbol{r}-i\omega_1 t}
$$
と表すことができるよ。同様に、媒質2中の進行波の波数ベクトル$${\boldsymbol{k}_2}$$と、反対向きに進行する波の波数ベクトル$${\boldsymbol{k}_2'}$$を
$$
\boldsymbol{k}_2 = k_2 (\sin\theta_2, 0, \cos\theta_2)
$$
$$
\boldsymbol{k}_2' = k_2' (\sin\theta_2', 0, -\cos\theta_2')
$$
と表した場合、媒質2の進行波$${\boldsymbol{A}_{21}}$$と後進波$${\boldsymbol{A}_{22} }$$は各偏光の振幅を用いて、
$$
\boldsymbol A_{21}=\left(\begin{matrix} a_{21}^{(p)} \cos\theta_2 \cr a_{21}^{(s)} \cr -a_{21}^{(p)} \sin\theta_2 \end{matrix}\right) e^{i \boldsymbol{k}_2 \cdot \boldsymbol{r}-i\omega_2 t}
$$
$$
\boldsymbol A_{22}=\left(\begin{matrix} -a_{22}^{(p)} \cos\theta_2' \cr a_{22}^{(s)} \cr -a_{22}^{(p)} \sin\theta_2' \end{matrix}\right) e^{i \boldsymbol{k}_2' \cdot \boldsymbol{r}-i\omega_2 t}
$$
と表すことができるね。また、各媒質における電磁波は進行波と後進波の和で表されるので
$$
\boldsymbol{A}_1 = \boldsymbol{A}_{11} + \boldsymbol{A}_{12}
$$
$$
\boldsymbol{A}_2 = \boldsymbol{A}_{21} + \boldsymbol{A}_{22}
$$
となるね。これらの表式から、境界面における電磁波の接続条件を導出することができるよ。
境界条件の導出
境界面ををまたぐ微小領域における電場・磁場・電束密度・磁束密度(境界条件は、$${\boldsymbol{E}, \boldsymbol{H}, \boldsymbol{D}, \boldsymbol{B}}$$)の満たすべき接続条件はマクスウェル方程式から直ちに次のように導かれるよ。
$${\boldsymbol{E}, \boldsymbol{H}}$$の境界面と平行成分が連続
$${\boldsymbol{D}, \boldsymbol{B}}$$の境界面と垂直成分が連続
初めに$${\boldsymbol{E}}$$の境界面における接続について考えるね。媒質1と2の電場は、
$$
\boldsymbol E_{1}(\boldsymbol r,t) = i\omega _1\left(\begin{matrix} a_{11}^{(p)} \cos\theta_1 e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}} -a_{12}^{(p)} \cos\theta_1' e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}}\cr a_{11}^{(s)} e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}} + a_{12}^{(s)} e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}} \cr -a_{11}^{(p)} \sin\theta_1 e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}} -a_{12}^{(p)} \sin\theta_1' e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}} \end{matrix} \right) e^{-i\omega_1 t}
$$
$$
\boldsymbol E_{2}(\boldsymbol r,t) = i\omega _2\left(\begin{matrix} a_{21}^{(p)} \cos\theta_2 e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}} -a_{22}^{(p)} \cos\theta_2' e^{i\boldsymbol{k}_2'\cdot\boldsymbol{r}} \cr a_{21}^{(s)} e^{i\boldsymbol{k}_2\cdot\boldsymbol{r}} + a_{22}^{(s)} e^{i\boldsymbol{k}_2'\cdot\boldsymbol{r}} \cr -a_{21}^{(p)} \sin\theta_2 e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}} -a_{22}^{(p)} \sin\theta_2' e^{i\boldsymbol{k}_2'\cdot\boldsymbol{r}} \end{matrix} \right) e^{-i\omega_2 t}
$$
となるね。境界面上の任意の位置$${(x,y,0)}$$で、境界面と並行成分が連続$${\boldsymbol{E}_{1\|}(x,y,z=0;t)=\boldsymbol{E}_{2\|}(x,y,z=0;t)}$$であることが接続条件だね。$${y}$$成分が連続である条件からは
$$
a_{11}^{(s)} e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}+a_{12}^{(s)} e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}} = a_{21}^{(s)} e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}+a_{22}^{(s)} e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}}
$$
が得られるね。境界面上のすべての点$${(x,y,0)}$$で成り立つためには、
$$
a_{11}^{(s)}+a_{12}^{(s)} = a_{21}^{(s)}+a_{22}^{(s)}
$$
$$
k_1\sin\theta_1 = k_2\sin\theta_2
$$
$$
k_1=k_1' \ , \ k_2=k_2'
$$
を満たす必要があるね。$${k_1 = |\boldsymbol{k_1}|, k_2 = |\boldsymbol{k_2}| }$$だよ。第2式は「スネルの法則」って呼ばれる有名な関係式だね。この法則は波数は境界面の並行方向成分が一致する(波が境界面上で連続)という意味をもつよ。スネルの法則は屈折率を用いて
$$
n_1\sin\theta_1 = n_2\sin\theta_2
$$
となり、$${\theta_1}$$と$${\theta_2}$$の関係もこの式で決定されるよ。次に、$${x}$$成分を比較すると
$$
(a_{11}^{(p)}-a_{12}^{(p)})\cos\theta_1 = (a_{21}^{(p)}-a_{22}^{(p)})\cos\theta_2
$$
が得られるよ。
続いて、$${\boldsymbol{D}}$$の境界面における接続を$${\boldsymbol{D} = \epsilon_0\epsilon \boldsymbol{E}}$$を考慮して考えよ。$${z}$$成分が境界面上のすべての点$${(x,y,0)}$$で連続となるためには、
$$
\epsilon_1(a_{11}^{(p)}+a_{12}^{(p)})\sin\theta_1 = \epsilon_2(a_{21}^{(p)}+a_{22}^{(p)})\sin\theta_2
$$
$$
\sqrt{\epsilon_1\mu_1}\sin\theta_1 = \sqrt{\epsilon_2\mu_2}\sin\theta_2
$$
を満たす必要があるね。この2つの式を組み合わせると、
$$
\sqrt{\frac{\epsilon_1}{\mu_1}}(a_{11}^{(p)}+a_{12}^{(p)})= \sqrt{\frac{\epsilon_2}{\mu_2}}(a_{21}^{(p)}+a_{22}^{(p)})
$$
が得られるね。
次に$${\boldsymbol{B}}$$の境界面における接続について考えるよ。$${\boldsymbol{B}}$$は$${\boldsymbol{B} = \nabla \times \boldsymbol{A} = i\boldsymbol{k} \times \boldsymbol{A}}$$の関係を用いて、
$$
\boldsymbol{B}_{1}(\boldsymbol{r},t) = i\left(\begin{matrix} (-a_{11}^{(s)}\,e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}+a_{12}^{(s)}\,e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}})\,k_1 \cos\theta_1\cr a_{11}^{(p)}\, k_1 \,e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}+a_{12}^{(p)}\, k_1 \,e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}} \cr (a_{11}^{(s)}\,e^{i\boldsymbol{k}_1\cdot\boldsymbol{r}}+a_{12}^{(s)}\,e^{i\boldsymbol{k}_1'\cdot\boldsymbol{r}})\,k_1 \sin\theta_1 \end{matrix} \right) e^{-i\omega_1 t}
$$
$$
\boldsymbol{B}_{2}(\boldsymbol{r},t) = i\left(\begin{matrix} (-a_{21}^{(s)}\,e^{i\boldsymbol{k}_2\cdot\boldsymbol{r}}+a_{22}^{(s)}\,e^{i\boldsymbol{k}_2'\cdot\boldsymbol{r}})\,k_2 \cos\theta_2\cr a_{21}^{(p)}\, k_2 \,e^{i\boldsymbol{k}_2\cdot\boldsymbol{r}}+a_{22}^{(p)}\, k_2 \,e^{i\boldsymbol{k}_2'\cdot\boldsymbol{r}}\cr (a_{21}^{(s)}\,e^{i\boldsymbol{k}_2\cdot\boldsymbol{r}}+a_{22}^{(s)}\,e^{i\boldsymbol{k}_2'\cdot\boldsymbol{r}})\,k_2 \sin\theta_2 \end{matrix} \right) e^{-i\omega_2 t}
$$
と表すことができるね。$${\boldsymbol{B}}$$の$${z}$$成分の接続条件から、
$$
k_1\sin\theta_1(a_{11}^{(s)}+a_{12}^{(s)}) = k_2\sin\theta_2(a_{21}^{(s)}+a_{22}^{(s)})
$$
$$
a_{11}^{(s)} + a_{12}^{(s)} = a_{21}^{(s)} + a_{22}^{(s)}
$$
が得られね。先のスネルの法則を考慮すると、この2つの式は同じだね。
最後に$${\boldsymbol{H}}$$の境界面における接続$${\boldsymbol{H} = 1/\mu_0\mu \boldsymbol{D}}$$を考慮して、境界面上の任意の位置($${(x,y,0)}$$)で、境界面と並行成分が連続となるための条件$${\boldsymbol{H}_{1\|}(x,y,z=0;t)=\boldsymbol{H}_{2\|}(x,y,z=0;t)}$$を課す必要があるね。$${x}$$成分が連続である条件から、
$$
\frac{1}{\mu_0\mu_1} \left\{ k_1 \cos\theta_1(-a_{11}^{(s)}+a_{12}^{(s)}) \right\}=\frac{1}{\mu_0\mu_2} \left\{ k_2 \cos\theta_2(-a_{21}^{(s)}+a_{22}^{(s)}) \right\}
$$
が得られ、$${k_1/k_2=\sqrt{\mu_1\epsilon_1}/\sqrt{\mu_2\epsilon_2}}$$を考慮すると
$$
\sqrt{\frac{\epsilon_1}{\mu_1}} \cos\theta_1(-a_{11}^{(s)}+a_{12}^{(s)}) =\sqrt{\frac{\epsilon_2}{\mu_2}} \cos\theta_2(-a_{21}^{(s)}+a_{22}^{(s)})
$$
となるね。次に、$${y}$$成分が連続である条件から、
$$
\frac{1}{\mu_0\mu_1} \left\{ k_1 (a_{11}^{(p)}+a_{12}^{(p)}) \right\} = \frac{1}{\mu_0\mu_2} \left\{ k_2(a_{21}^{(p)}+a_{22}^{(p)}) \right\}
$$
が得られるのだけれども、これは先に導出した条件と一致するね。以上を整理すると、$${s}$$偏光に関しては
$$
a_{11}^{(s)}+a_{12}^{(s)} = a_{21}^{(s)}+a_{22}^{(s)}
$$
$$
\sqrt{\frac{\epsilon_1}{\mu_1}} \cos\theta_1(a_{11}^{(s)}-a_{12}^{(s)}) =\sqrt{\frac{\epsilon_2}{\mu_2}} \cos\theta_2(a_{21}^{(s)}-a_{22}^{(s)})
$$
となり、また、$${p}$$偏光に関しては
$$
\sqrt{\frac{\epsilon_1}{\mu_1}} (a_{11}^{(p)}+a_{12}^{(p)})=\sqrt{\frac{\epsilon_2}{\mu_2}} (a_{21}^{(p)}+a_{22}^{(p)})
$$
$$
(a_{11}^{(p)}-a_{12}^{(p)})\cos\theta_1 = (a_{21}^{(p)}-a_{22}^{(p)})\cos\theta_2
$$
が得られるね。これらの得られた関係式を見ると、物質定数$${\mu, \epsilon}$$は必ず$${\sqrt{\epsilon/\mu}}$$の形であらわれているね。つまり、境界面での振舞いはインピーダンス$${Z\equiv\sqrt{\mu/\epsilon}}$$で定義される量が重要となるわけだね。媒質1,2におけるインピーダンスを真空のインピーダンスを$${Z_0}$$として
$$
Z_1:=\sqrt{\frac{\mu_1}{\epsilon_1}}Z_0\ , \ Z_2 \equiv \sqrt{\frac{\mu_2}{\epsilon_2}}Z_0
$$
と表すと、4つの関係式は次のようにまとめられるね。
$$
a_{11}^{(s)}+a_{12}^{(s)} = a_{21}^{(s)}+a_{22}^{(s)}
$$
$$
\frac{\cos\theta_1}{Z_1}(a_{11}^{(s)}-a_{12}^{(s)}) = \frac{\cos\theta_2}{Z_2}(a_{21}^{(s)}-a_{22}^{(s)})
$$
$$
\frac{1}{Z_1} (a_{11}^{(p)}+a_{12}^{(p)}) = \frac{1}{Z_2} (a_{21}^{(p)}+a_{22}^{(p)})
$$
$$
\cos\theta_1(a_{11}^{(p)}-a_{12}^{(p)}) = \cos\theta_2(a_{21}^{(p)}-a_{22}^{(p)})
$$
通常の誘電体を考える場合、比透磁率は$${\mu\simeq1}$$であるため、$${Z=1/n}$$の関係があるよ。
$${s}$$偏光における関係式と$${p}$$偏光における関係式はそれぞれ4つの未知の量に対して方程式が2つなので、媒質2における振幅$${a_{21}, a_{22}}$$を媒質1における振幅$${a_{11}, a_{12}}$$で表すことができるね。$${s}$$偏光については、
$$
a_{21}^{(s)} = \frac{1}{2} \left[ (1+\frac{Z_2}{Z_1}\frac{\cos\theta_1}{\cos\theta_2})a_{11}^{(s)} +(1 - \frac{Z_2}{Z_1}\frac{\cos\theta_1}{\cos\theta_2})a_{12}^{(s)} \right]
$$
$$
a_{22}^{(s)} = \frac{1}{2} \left[ (1-\frac{Z_2}{Z_1}\frac{\cos\theta_1}{\cos\theta_2})a_{11}^{(s)} +(1 + \frac{Z_2}{Z_1}\frac{\cos\theta_1}{\cos\theta_2})a_{12}^{(s)} \right]
$$
となって、$${p}$$偏光については、
$$
a_{21}^{(p)} = \frac{1}{2} \left[ (\frac{Z_2}{Z_1} + \frac{\cos\theta_1}{\cos\theta_2})a_{11}^{(p)} +(\frac{Z_2}{Z_1}-\frac{\cos\theta_1}{\cos\theta_2})a_{12}^{(p)} \right]
$$
$$
a_{22}^{(p)} = \frac{1}{2} \left[ (\frac{Z_2}{Z_1} - \frac{\cos\theta_1}{\cos\theta_2})a_{11}^{(p)} + (\frac{Z_2}{Z_1}+\frac{\cos\theta_1}{\cos\theta_2})a_{12}^{(p)} \right]
$$
となるね。
透過係数と反射係数

以上の結果を踏まえて、上図のように単一境界面のみ存在する場合の媒質1から媒質2への入射に対する透過係数と反射係数を導出することができるよ。$${a_{11}}$$を入射波とした場合、$${a_{12}}$$と$${a_{21}}$$がそれぞれ反射波と透過波となるね。また、$${a_{22}=0}$$だね。$${s}$$偏光の反射率と透過率をそれぞれ$${r{^{(s)}}$$、$${t^{(s)}$$で表すと、
$$
r^{(s)} = \frac{a_{12}^{(s)}}{a_{11}^{(s)}} = \frac{-Z_1\cos\theta_2+Z_2\cos\theta_1}{Z_1\cos\theta_2+Z_2\cos\theta_1}
$$
$$
t^{(s)} = \frac{a_{21}^{(s)}}{a_{11}^{(s)}} = \frac{2Z_2\cos\theta_1}{Z_1\cos\theta_2+Z_2\cos\theta_1}
$$
となるね。同様に、$${p}$$偏光の反射率と透過率をそれぞれ$${r^{(p)}}$$、$${t^{(p)}}$$で表すと、
$$
r^{(p)} = \frac{a_{12}^{(p)}}{a_{11}^{(p)}} = \frac{-Z_2\cos\theta_2+Z_1\cos\theta_1}{Z_1\cos\theta_1+Z_2\cos\theta_2}
$$
$$
t^{(p)} = \frac{a_{21}^{(p)}}{a_{11}^{(p)}} = \frac{2Z_2\cos\theta_1}{Z_1\cos\theta_1+Z_2\cos\theta_2}
$$
となるね。ちなみに透過係数と反射係数の間には次の関係もあるよ。
$$
t^{(s)}_{12} - r^{(s)}_{12} = 1
$$
$$
\frac{Z_1}{Z_2}\,t^{(p)}_{12} - r^{(p)}_{12} = 1
$$
境界面が1つの場合、透過係数$${r}$$並びに反射係数$${t}$$は入射波の角度$${\theta_1}$$に依存する一方で、周波数$${\omega}$$(波長$${\lambda}$$)には依存しないね。
反射係数と透過係数の角度依存性
外部反射($${n_1<n_2}$$)の場合

上図は$${n_1=1,n_2=2}$$のときの透過係数と反射係数の入射角度依存性だよ。$${s}$$偏光の場合、透過係数は単調減少、反射係数は単調増加なのだけれども、$${p}$$偏光の場合には、反射係数が0となるブリュースター角($${\theta_B}$$)と呼ばれる角度が存在するよ。$${r^{(p)}=1}$$より
$$
\theta_B = \tan^{-1}\left( \frac{n_2}{n_1} \right)
$$
となるね。
内部反射($${n_1>n_2}$$)の場合

上図は$${n_1=2,n_2=1}$$のときの透過係数と反射係数の入射角度依存性だよ。屈折率が大きな領域から小さな領域への入射の場合、特定の入射角度以上で全反射する臨界角度$${\theta_C}$$が存在するよ。
$$
\theta_C = \sin^{-1}\left( \frac{n_2}{n_1} \right)
$$
透過係数は$${s}$$偏光も$${p}$$偏光も臨界角度まで単調増加、臨界角度以降は単調減少しているのに対して、反射係数はブリュースター角の存在する$${p}$$偏光は一度0まで下がるけれども、$${s}$$偏光とともに臨界角度で1となり、それ以降はずっと1のままだね。
プログラムソース:Python
次の動画を作成したプログラムソースを以下に示すよ。もし良かったら試してみてくださーい!
#################################################################
## 透過係数と反射係数
#################################################################
import numpy as np
import scipy.integrate as integrate
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import colorsys
#図全体
fig = plt.figure(figsize=(12, 8))
#全体設定
plt.rcParams['font.family'] = 'Times New Roman' #フォント
plt.rcParams['font.size'] = 16 #フォントサイズ
plt.rcParams["mathtext.fontset"] = 'cm' #数式用フォント
#カラーリストの取得
colors = plt.rcParams['axes.prop_cycle'].by_key()['color']
#虚数単位
I = 0.0 + 1.0j
######################################
# 物理定数
######################################
#光速
c = 2.99792458E+8
#真空の透磁率
mu0 = 4.0 * np.pi * 1.0E-7
#真空の誘電率
epsilon0 = 1.0/(4.0*np.pi*c*c)*1.0E+7
######################################
# 物理系の設定
######################################
#電磁波の波長
lambda_ = 500.0E-9
#波数
k = 2.0 * np.pi / lambda_
#屈折率
n1 = 1.0
n2 = 2.0
#ブリュースター角
thetaB = np.arctan( n2 / n1 )
print("ブリュースター角:" + str( thetaB / np.pi * 180 ))
thetas = np.arange(0, 90+0.01, 0.01)
#インピーダンス
Z1 = 1.0 / n1
Z2 = 1.0 / n2
##########################################################
#描画用リスト
xl = []
rsl = []
tsl = []
rpl = []
tpl = []
#gamma による違い
for theta in thetas:
theta1 = theta * np.pi / 180
#波数
k1 = n1 * k
k2 = n2 * k
sin1 = np.sin(theta1)
cos1 = np.cos(theta1)
sin2 = n1/n2 * sin1
cos2 = np.sqrt(1.0 - sin2**2) if sin2 <= 1 else np.sqrt( sin2**2 - 1 ) * 1j
rs = (-Z1 * cos2 + Z2 * cos1) / (Z1 * cos2 + Z2 * cos1)
ts = ( 2.0 * Z2 * cos1) / (Z1 * cos2 + Z2 * cos1)
rp = (-Z2 * cos2 + Z1 * cos1) / (Z1 * cos1 + Z2 * cos2)
tp = ( 2.0 * Z2 * cos1) / (Z1 * cos1 + Z2 * cos2)
#print( ts - rs )
#print( Z1/Z2 * tp - rp )
xl.append( theta )
rsl.append( np.abs(rs) )
tsl.append( np.abs(ts) )
rpl.append( np.abs(rp) )
tpl.append( np.abs(tp) )
#################################################################
# グラフの設定
#################################################################
#グラフタイトルと軸ラベルの設定
plt.title( "透過係数と反射係数の大きさ(" + r"$n_1=$" +str(n1) + r"$, n_2 =$" +str(n2) + ")", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.xlabel( r"$\theta\,[{}^\circ]$", fontname="Yu Gothic", fontsize=20, fontweight=500 )
plt.ylabel( "Intensity" , fontname="Yu Gothic", fontsize=20, fontweight=500 )
#罫線の描画
plt.grid( which = "major", axis = "x", alpha = 0.7, linewidth = 1 )
plt.grid( which = "major", axis = "y", alpha = 0.7, linewidth = 1 )
#描画範囲を設定
plt.xlim([0, 90])
plt.ylim([0, 1.1])
plt.plot(xl, rsl, linestyle='solid', linewidth = 4, label=r"$|r^{(s)}|$")
plt.plot(xl, tsl, linestyle='solid', linewidth = 4, label=r"$|t^{(s)}|$")
plt.plot(xl, rpl, linestyle='solid', linewidth = 4, label=r"$|r^{(p)}|$")
plt.plot(xl, tpl, linestyle='solid', linewidth = 4, label=r"$|t^{(p)}|$")
plt.legend()
#グラフの表示
plt.show()
