【Python MPS】粒子法でベルヌーイの定理の検証：トリチェリの原理

外力として重力（重力加速度$${g}$$）が与えられた完全流体が、高さ$${y}$$の地点で流速$${v^2}$$、圧力$${p}$$、密度$${\rho}$$ で与えられた場合、次の量が一定値となることが知られているね。

$$
p + \frac{1}{2} \rho v^2 + \rho g y =一定
$$

これは完全流体のエネルギー保存則に対応するベルヌーイの定理と呼ばれるね。この定理は非圧縮で粘性が無視できる場合の水力学や水理学で最も強力な定理として活用されているらしいね。本稿ではベルヌーイの定理の適用例一つであるトリチェリの定理を実験してみるよ。

トリチェリの定理の模式図

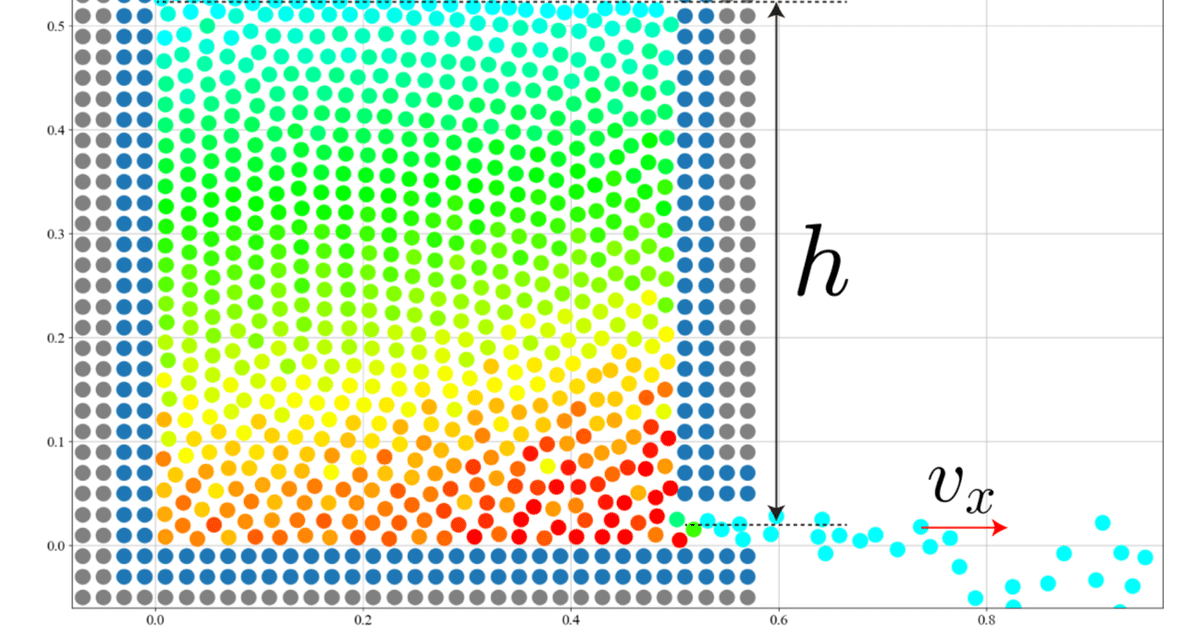
上図のように上面が大気圧にさらされた満水の容器の下部に小さな穴を開けたとするね。水は勢いよく噴射するのだけれども、水面から穴までの距離$${h}$$ としたときに水流の速度 $${v_x}$$ は次の式で与えられるよ。

$$
v_x =\sqrt{2gh}
$$

この関係式は大気圧の変化が高さ $${h}$$ で無視できる場合にベルヌーイの定理から直ちに導かれるね。さっそくこの前に作った粒子法アルゴリズム（MSP法）で実験してみよう！

下の図は、横軸に高さ$${h}$$、縦軸に流出速度$${v_x}$$だよ。実線は先のトリチェリの定理の式で与えられる値だね。この程度の粗い実験でも概ね再現できているね。

トリチェリの定理の検証

これからもどんどん勉強していくよ。応援してください！

Pythonプログラム（粒子法：MSP法）

本実験のPythonnプログラムを販売いたします。良かったら遊んでみてください。なお、アルゴリズムの詳細はこちらにまとめているよ。