
レクチャー4:現価の計算
ひとことで言えば、ここまで見てきた利息の計算の逆を考えるのが現価計算です。現価は、「現在の価格」の略とおぼえてください。将来受け取る金額が先にわかっていて、利息分を取り除いて、現在の価格を考えるわけです。
例によってやさしく表現した例題で考えてみましょう。
ちょっと不自然ですが…
【例題4】
あなたが利率10%で貸したお金が1年後に110万円になって返ってきました。いくら貸していたでしょうか?
いくら貸したかくらいおぼえているだろ、という真っ当なコメントはちょっとおいといて…図で示してみると…

イメージ図1とそっくりですね。ちょっと比べてみましょう。

ほとんど間違い探しです。
そう、変わったのは数カ所だけ、「→」が「←」になっただけですね。
そして「×」が「÷」になっていますね。ここがポイントです。
「元本100万円に(100%+10%)を掛けて、元利合計110万円」の逆をすればよい、つまり、元利合計110万円を(100%+10%)で割れば、元本100万円とわかります。
もうちょっと数学っぽく説明し直しましょう。
一番初めに出てきた【単利計算の公式】を思い出してみてください。
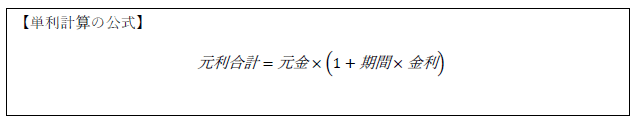
ここにわかっている数字を入れ込んでみましょう。
1年後に受け取れる金額は110万円、利率10%だから…

…となります。
赤の▢の部分が、図の「←」に当たるわけですね。
しっくりきたでしょうか。
今度はもっと長い期間でも考えてみましょう。
といっても同じパターンなので安心してください。
【例題5】
3年前にあなたが利率10%の複利で貸したお金が133万円になって返ってきました。いくら貸していたでしょうか?
またも無理のある設定ですが、3年も前に貸したのだから忘れていても仕方がないということにしてください。図で示してみると…

今度はイメージ図2とそっくりですね。ちょっと比べてみましょう。

今回も、そう、変わったのは「→」が「←」になっただけですね。
そして「×」が「÷」になっていますね。ここがポイントでした。先程の応用です。
「元本100万円に(100%+10%)を3回掛けて、元利合計133万円」の逆をすればよい、つまり、元利合計133万円を(100%+10%)で3回割れば、元本100万円とわかります。
では、さっそく数式にしてみましょう。
3年後に受け取った金額(元利合計)は133万円、利率10%だから…

…と計算することになります。
金利の計算の逆をするのが現価計算なので、
将来受け取れる金額に対して、貸している年数分、(100%+10%)で割るわけですね。ここから導ける公式はこうなります。

改めて、公式に当てはめて計算してみましょう。
【例題5】
3年前にあなたが利率10%の複利で貸したお金が133万円になって返ってきました。いくら貸していたでしょうか?
元利合計133万円、利率は10%、年数は3年なので…

さて、この数式の中から、赤の▢の部分だけを抜き出したのが、「現価係数」です。「貸したお金が現在いくらの価格になるかわかる係数」の略とおぼえましょう。

仕上げに、現価係数の表を使った計算も練習しておきましょう。
例題5をもう一度考えてみましょう。
【例題5】
3年前にあなたが利率10%の複利で貸したお金が133万円になって返ってきました。いくら貸していたでしょうか?

現価係数を使った計算、いかがだったでしょうか。
お分かりの通り、先程の計算式の青の▢の部分と同じですね。
現価係数を使うことで、ここでも面倒な累乗の計算をスキップすることができたわけです。
最後に演習問題を解いて、レクチャー4はおしまいです。
お疲れ様でした。



【免責事項】
<転載の禁止について>
当サイトに存在する、文章や画像、動画等の著作物の情報を転載することを禁止します。
<当サイトの情報の正確性について>
当サイトのコンテンツや情報において、可能な限り正確な情報を掲載するよう努めています。しかし、誤情報が入り込んだり、情報が古くなったりすることもあります。必ずしも正確性を保証するものではありません。
<損害等の責任について>
当サイトに掲載された内容によって生じた損害等の一切の責任を負いかねますので、ご了承ください。
また当サイトからリンクやバナーなどによって他のサイトに移動された場合、移動先サイトで提供される情報、サービス等について一切の責任も負いません。当サイトを利用する場合は、自己責任で行う必要があります。
*****関連リンク*****
