
黄金数…贅沢な名だねぇ。【数学解説#2】
【はじめに】
こんにちは、ぱぺです。
数学解説第2弾!
今回は黄金数の特徴について話していきます!
結構な長編となるので、閲覧頑張ってください! (おい
【 黄金数 の解説】
今回の解説対象は 黄金数 です!
〈必要知識〉
今回の解説を読むときに必要な知識としては、
比例式 (中1)
平方根 (中3)
二次方程式 (中3)
三角形の相似 (中3)
極限 (高校Ⅲ)
正則連分数展開 →後に簡単に解説します
フィボナッチ数 →後に簡単に解説します
〈黄金数とは〉
今回解説する黄金数、どんな値なのでしょうか。

うーん…見ただけでは、この値がどれだけなのか分からないですよね。
近似値としては、1.61803398874989484… です。
「1.618」くらいは覚えておきましょう。
この数は 円周率のπ , ネイピア数のe , 純虚数のi と同じように、
黄金比にも数学定数として文字が決まっています!
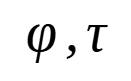
φ (ファイ)、またはτ(タウ)です。
僕はよく「φ」の大文字「Φ」の方を斜字体で使います。

ちなみにですが、それぞれの文字の名づけの理由は、
「φ」
→紀元前5世紀、パルテノン神殿に黄金比を使って分割をした古代ギリシアの彫刻家フィディアス(英語:Pheidias,ギリシャ語:Φειδίας)の頭文字を取った
「τ」
→黄金比に関連した、「黄金分割」という分割方法から「分割」「切断」を意味するギリシャ文字が「τ」(らしい)
という感じです。
〈黄金数の特徴① 正五角形〉
正五角形の何が黄金数かというと、それはズバリ、「対角線」です。

上図をご覧ください。
正五角形ABCDEの一辺の長さを1,対角線の長さをmとします。
AD,BD,CEを引き、ADとCEの交点をH,BDとCEの交点をIとすると、このようになります。
「・」の角度は36°,「○」の角度は72°であり、△ADEと△CDIはそれぞれ底角の等しい二等辺三角形なので相似です。また、△BICは二等辺三角形だからBI=1となります。
では、相似比はいくらでしょう。
まず、DI=BD-BI=m-1となりますね。線分の相似比はm:1であり、1:(m-1)でもあるので、比例式m:1=1:(m-1)を解きます。
m(m-1)=1
m²-m-1=0
m=(1±√5)/2
mは線分の長さなので、m>0より、m=(1+√5)/2に限定されます。
(1+√5)/2=φですので、正五角形の対角線の長さはφになります!
まさにヘッダーにあるような図形の関係なのです!

〈黄金数の特徴② 方程式〉
特徴①のところで出てきました、
m²-m-1=0
この解にm=φが含まれるわけですね。
つまり、この方程式にm=φを代入したこの式、

が成り立つわけですね!
そして、この式を変形して

とできます。
これは特徴③~⑥でも出てくるので、覚えておいてください。
〈黄金数の特徴③ 平方根マトリョーシカ〉
「平方根マトリョーシカ」
聞いたことないという人しかいませんよね。
だって僕が勝手に名付けたんだもん((殴

「えぇ…」ってなりますね。
こんなめんどくさい式がまさかの黄金数になるんです。
これはなぜなんでしょう。
特徴②で、φ²=φ+1が成り立つと言っていましたが、この式を今回使います。
φ>0であることを確認しているのは、√をしたときに+√になるか-√になるかを確かめるためです。

このように、φ=√(1+φ)の+φの部分に、さらにφ=√(1+φ)を代入して、
さらにその+φの部分にφ=√(1+φ)を代入して、、、
というようにしていくと、このようなマトリョーシカになるわけですね。
〈黄金数の特徴④ 正則連分数〉
えっ、正則連分数? なにそれ?
と思う人は少なからずいるかと思われます。
ここでとりあえず簡単に解説します。
まず連分数というのは、分母に分数を組み込んでいったような形のことを言います。
正則連分数は、連分数の中に組み込んだすべての分数の分子を1にした形を言います。
とは言っても、これじゃわかりませんよね。ということで、例示します。
今ここに、24/7という分数があります。

この数を、帯分数のように 整数+(1以下の分数)の形にします。

3/7は1以下の分数ですね。
今回は分子を1にしたいので、分母は7/3
これも同じように 整数+(1以下の分数)の形にします。

1/3は既に1以下の、分子が1の分数ですので、これが正則連分数です!
では、φを正則連分数にするとどうなるんでしょう。

こんな感じで、φ=1+1/φの右辺のφに、さらにφ=1+1/φを代入して、
さらにその右辺のφにφ=1+1/φを代入して、、、
というようにしていくと、このようなマトリョーシカになるわけですね。
…って、え??

全部1なの!?
はい、全部1だけなんですよ。なんてきれいなんでしょう。
〈黄金数の特徴⑤ 黄金長方形〉
黄金長方形とは何でしょうか。

この図のように、縦横比1:φの長方形のことを指します。
では、この長方形の特徴とは何でしょう。
①斜め折り
みなさん、A4用紙を出してください。
この折り方、皆さんも一度はやったことあるのではないでしょうか


辺が重なるように斜めに折る折り方です。
用紙が正方形でない限り、こう折ると長方形が余ってしまいます。
そして余った長方形でない、折った部分は正方形になっています(重要)。
これを黄金長方形でやってみましょう。

はい。これが何だ?と思う人もいるかもしれません。
では、この余った長方形の縦横比を見てみましょう。

1 : (φ-1)ですね。この比に何か特徴はないでしょうか。
φ-1がどんな値になるか考えてみましょう。

おやおや?? φ-1=1/φと出ました。
ということは…残ったあの長方形の縦横比は1:1/φ、つまりφ:1となります。
そしてこの長方形を90°回転させると縦横比1:φの長方形になるんですよね。

縦横比1:φの長方形ということは…黄金長方形ですよね?
ということは、ここからまた同じように正方形を作れますね。
黄金長方形から正方形を除くと黄金長方形が余り、その長方形から正方形を除くとまたもや黄金長方形が余ります。
とすると、黄金長方形は大きさの違う正方形を1つずつ敷き詰めたものでできているというわけです!

〈黄金数の特徴⑥ フィボナッチ数との関係 その1〉
フィボナッチって誰やねん!
まあそうなるでしょうね。フィボナッチが誰かは後で解説するとして、、、
とりあえずまずはこの「フィボナッチ数」について説明します。
皆さん、足し算はやったことありますよね。
[ 馬鹿にすんなよ } 読者
ならこの話は分かる筈です。
まず、この計算をしてください。

勿論、答えは2ですよね。では次に、この計算を。

答は3ですね。では今度はこれをやってみてください。

答は5ですね。ということで、要領はわかりましたかね?
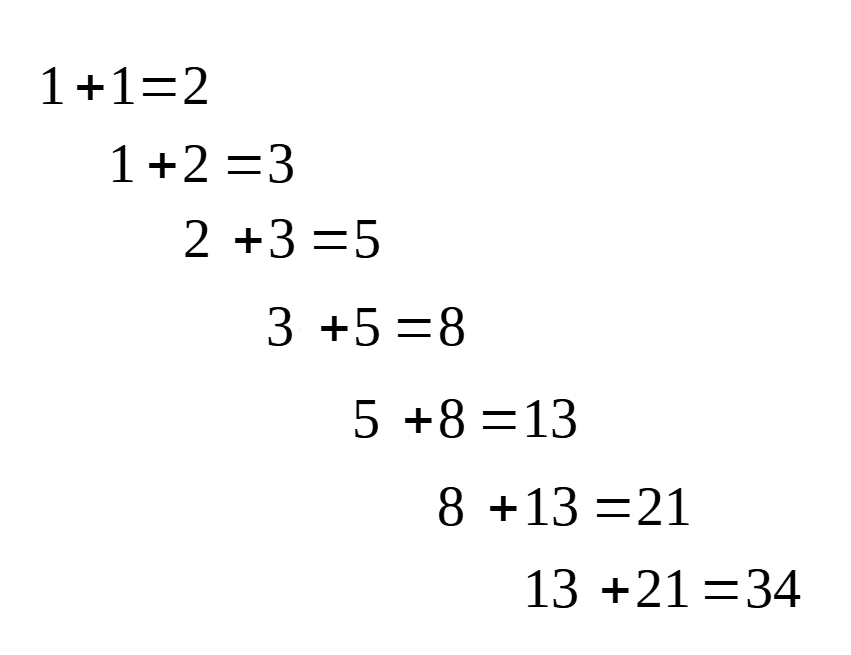
ひとつ前の足し算の足す数と答えの和を考えるんです。
そうして続けると…
1,1,2,3,5,8,13,21,34,55,89,144,233,…
というようになるんですね。これがフィボナッチ数です。
フィボナッチ数列の定義:初項, 第2項を1としたとき、直前の2つの項の和。
このフィボナッチ数列は、一般項というものがありまして、
「直前の2つの項の和がその項になる」ことから漸化式から求めると、
以下のようにできますねはい。

さて、さっき説明を後回しにしていたフィボナッチさん。
この人の本名はレオナルド・デ・ピサ(Leonardo de Pisa)、12世紀後半-13世紀前半を生きたイタリアの数学者で、ボナッチの息子(filius Bonacci)の略称からフィボナッチ(Fibonacci)と言われています。
さて、このフィボナッチ数と黄金数の特徴を紹介します。
適当に、隣り合うフィボナッチ数で割り算をしましょう。
5番目÷4番目 =5÷3 ≒1.6667
6番目÷5番目 =8÷5 =1.6
7番目÷6番目 =13÷8 =1.625
8番目÷7番目 =21÷13 ≒1.6154
9番目÷8番目 =34÷21 ≒1.6190
というように、計算してみます。

はい。とりあえずφとの差を見てみましょう。
だんだんと差が小さくなっているようですね。
これを無限にやっていくと、どんどんφに近づいていきます。
これは極限で求められますね。

まあこんな感じでφが出てきます。
3行目から4行目で-1と+φを消したのは、n→∞のとき
(-1)^(n+1) φ^(2n+2) と (-1)^(n+1) φ^(2n+1)の絶対値が無限に大きくなってしまうからですね。-1や+φなどは膨大な数の前では塵と化すのです。
〈黄金数の特徴⑥ フィボナッチ数との関係 その2〉
√2などの、平方根を用いた式は何乗しても1次式で表されます。
とにかく例を見てみましょう。

上の画像は2+√3の累乗を、(2+√3)の形を使って1次式のようにあらわしたものです。勿論黄金比も例外ではなく、累乗を1次式の形で表せます。
試しに計算してみましょう。
これの計算は、あの時の式(②)を使えばいいです。

例えば、φ^3の場合はこういう計算です。

となります。こんな感じでφの累乗は…

となります。ここで、φの係数と定数に注目しましょう。
0,1,1,2,3,5,…と1,0,1,1,2,3,…と並んでいますね。
これ、前に見たことありません?
そう、フィボナッチ数です!!
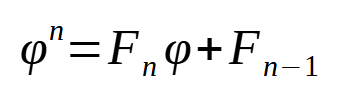
なんかスッキリした形になりましたね。
そう。フィボナッチ数の定義にφが出てきて、φの累乗にフィボナッチ数が出てくるんです。不思議ですね。
【おわりに】
いかがだったでしょうか。8月中旬に第1回をやったはずなのにいつのまにか第2回が10月になってしまうというMISTAKESが発生してました。申し訳ありません。早くても第3回は10月の下旬になるでしょうね。
【次回予告】
次回、第3回の数学解説のテーマは…
-エジプト分数-
1/a+1/b=1とかの問題の解法をまとめます。(2023/9/10)
【参考文献】
新学習指導要領における算数・数学内容系統一覧表
https://www.shinko-keirin.co.jp/keirinkan/topics/2011/data/math_keitouhyo.pdf
意外なところに黄金分割
http://shochandas.xsrv.jp/ratio/goldensection.htm
デザインを美しくする「黄金比」について理解しよう!(身の回りにある黄金比)
https://www.asobou.co.jp/blog/web/golden-rate
フィボナッチ数列とは -コトバンク
https://kotobank.jp/word/%E3%83%95%E3%82%A3%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81%E6%95%B0%E5%88%97-615599
フィボナッチとは -コトバンク
https://kotobank.jp/word/%E3%83%95%E3%82%A3%E3%83%9C%E3%83%8A%E3%83%83%E3%83%81-122731
