【読了】いちばんやさしい医療統計
はじめに
以下を理解した時、ブレイクスルーが起きた
・母集団と標本の関係
・誤差の概念(そもそも誤差があるので統計を使う必要が出てくる)
Ⅰ 統計の役割
よくある誤解(P値の濫用)
・統計解析とは、仮説検定を行なってP値を算出すること(どんな解析手法を使ってもP値は算出可能)
・P値が0.05を下回れば良い結果が出ていることを示している(P値は単純に解釈可能)
統計の役割
①要約:標本の特徴把握
②推定:母集団の推定
統計の「計」は計画の「計」
・目的に対応するデータを収集できなければ意味のある使い方ができない(目的も解らず収集されたデータを使って、どういう分析結果を出そうかと考えるのは、捏造に繋がる)
・必要なデータを取るための計画を考えるところから統計業務は始まる
代表的なデータ種別と要約統計量
・連続データ:平均値、標準偏差、標準誤差、中央値、四分位範囲、95%信頼区間
・離散データ(カテゴリカルデータ):例数、件数、割合
・生存時間データ:中央値、95%信頼区間
・カウントデータ:総件数、一定時間あたりの件数、発生例数
例数と件数
・被験者が100人いて、1人に対して3回の処置を行った場合:例数(Cases)は100、件数(Events)は300
母集団の推定
・母集団の平均値は必ず単一の値に確定する(真値)
・母集団から抽出した標本の平均値はバラつく
※各標本のサンプルサイズ(標本数ではない)を大きくすると、標本平均の分布は正規分布に近づく(中心極限定理)
II 要約統計量
連続データ
・間隔尺度(Interval Scale):
・比率尺度(Ratio Scale):
標本の特徴を把握する
・まずはヒストグラムを作ってみる:入手したデータのバラつきに特徴を見出せる(正規分布なのか?一様分布なのか?歪んでいるのか?)
典型的な代表値
・平均値:分布が左右対称でない場合(例:外れ値がある)、代表的とは見做せない
・中央値:カテゴリカルデータの場合、意味がない
・最頻値:カテゴリカルデータの場合でも使える
典型的なバラつき指標
・分布が左右対称である場合:分散、標準偏差
・分布が左右対称ではない場合:四分位数(quartile)
※第2四分位数(Q2)と中央値は同じ意味、前半データに対する中央値がQ1、後半データに対する中央値がQ3になる。Q1-Q3の3点でデータ全体が4分割される
・分布が左右対称である場合:平均値μと標準偏差σを示す
・分布が左右対称ではない場合:平均値だけではなく中央値も示す、標準偏差ではなく箱ひげ図を使う
離散データ(カテゴリカルデータ)
離散データ(カテゴリカルデータ)
・数値化できないデータ
・数値化してもその間隔に意味がないデータ
・順序に意味がある場合:順序尺度(Ordinal Scale)
・順序に意味がない場合:名義尺度(Nominal Scale)
カテゴリカルデータの要約方法は2種類のみ
・数をカウントする
・カテゴリ内で割合を算出する(クロス集計表を作る)
III 統計的推測
点推定から区間推定への拡張
標本誤差の代わりに信頼区間を示す
・母平均と標本平均は異なる
・標本平均はバラつく
以上の性質から、母平均は単一の値で推定する(点推定)だけでなく、区間で推定する(区間推定)ことを組み合わせた方が合理的だとわかる
仮説検定
・有意差あり/有意差なしのいずれかの結論を得るための手法
・P値は確率を表しているだけ
・一般的には「A群とB群には差がない」という帰無仮説を設定し、P値が有意水準よりも低いことを示し、帰無仮説を棄却して「A群とB群には差がある」と結論する(どれくらい差があるかには言及できない)
αエラー/βエラー
製薬プロセスにおける臨床試験(特に第3相P3などの検証的試験)では、エラー確率の目安が慣例的に決まっている
・αエラー率:5%
・βエラー率:10-20%
αエラー率が高いと、効果がないものを誤って効果ありと判定してしまう(患者は効果を得られない)
βエラー率が高いと、効果があるものを誤って効果なしと判定してしまう(製薬メーカーは薬を申請できない)
そのため、αエラーの方が厳しい基準値(一般的に規制当局が要請している)になっている
βエラーを小さくするためには、必要な症例数が増えるため、開発コストが上がる
有意水準
臨床試験における有意水準は、ICHガイドラインのTechnical Requirement(ICH E9)で以下のように定められている
・片側検定の場合:片側2.5%
・両側検定の場合:両側5.0%
実務的に、臨床試験では片側検定(新薬がプラセボよりも効果あるか)の結果にしか興味がないが、なぜか慣例的に両側検定を行なっている
パラメトリック検定/ノンパラメトリック検定
・パラメトリック検定:母集団が「何らかの分布」に従うことを前提としている検定
・t検定(正規分布)
・二項検定(二項分布)
・ポアソン検定(ポアソン分布)
・CochranのQ検定(二項分布)
・Χ二乗適合度検定(Χ二乗分布)
・ロジスティック回帰(ロジスティック分布)
・ポアソン回帰(ポアソン分布)
・ノンパラメトリック検定:母集団分布について制約がない検定
・Wilcoxon順位和検定
理論的には、母集団分布を仮定せず、常にノンパラメトリック検定を行なっても良い
しかし実務的には、計画段階で症例数を決めるために母集団分布を設定するので、それを使ってパラメトリック検定を行うことが多い(明らかに分布が仮定できない場合にはノンパラメトリック検定を使う)
P値(有意確率)
・ある事象が起こる確率(Probability)
・ここで事象とは、帰無仮説が正しいと仮定した場合に、検定統計量の実現値として、いま得られている値(またはより極端な値)が観測されるという事象
※「帰無仮説が正しい確率」ではなく、「あるデータが観測される確率」である
・数学的には、検定統計量分布(確率分布)における面積を示す
P値が非常に小さい(p<有意水準α)場合、以下の理由が考えられる
①非常に稀な事象が発生した
②仮定(帰無仮説が正しい)に誤りがあった
仮説検定では、②の考え方により、対立仮説が正しいと主張する
「(統計的に)有意差あり」≠「(臨床的に)意味がある」
P値が小さい(統計的に「有意差がある」)からといって、それがすなわち臨床的に「意味がある」とは限らない
なぜなら、以下の要因でP値は小さくなるため
①まぐれ
②サンプルサイズが大きい(症例数が多い)
③バイアスが隠れている
④本当に効果がある(臨床的に「意味がある」)
極端に言えば、膨大なコストを投じてサンプルサイズを増やせさえすれば、たとえ臨床的に意味のない効果(例:この薬を飲むと、血圧が0.0001mmHg下降する)についても、統計的には「有意差あり」という結論を出すことはできる
逆に、臨床的に意味がある効果があっても、症例数不足により統計的有意差は主張できない(P値を計算しても小さい値にならない)場合もある
この場合は、次の研究で症例数を増やせばOK
実務的には、実験計画の段階で、必要サンプル数(統計的有意差を出すためには最低何個の症例数が必要なのか)を算出しておく
サンプルサイズ設計の重要性
サンプルサイズでP値は操作できてしまうので、
事前に既知情報から効果量を設定し、効果量、有意差、検出力を基にサンプルサイズを算出すべき
IV 計画を立てることの重要性
①バイアスを避ける
②精度を確保する
バイアスを避ける
バイアスは全てのステップで混入するため、混入を減らすための対策を計画に組み込む必要がある
①計画
②実施
③解析
④結論
バイアスの種類
・選択バイアス(Selection Bias):母集団から偏った標本を取得してしまうことによる
・情報バイアス(Information Bias):不利な情報が入手できないことによる(例:健康に気を遣っている人からは、気を遣っていない人よりも、申告するデータが多くなる)
・交絡バイアス(Confounding Bias):交絡因子が存在することによる(例:高血圧な人は高収入である)
基本的に、関心事以外の条件は同じにする努力が必要
精度を確保する
信頼区間を狭くするために、
・標本誤差を小さくする(測定方法を厳密に揃える)
・サンプルサイズを多くする
バイアスを減らす計画
①無作為抽出:(Random Sampling)母集団から無作為抽出することで、選択バイアスを減らせる
②無作為割り付け(Random Assignment):介入対象をランダムに決めることで、交絡バイアスを減らせる
③盲目化(Blinding):非盲検/単盲検/二重盲検により、情報バイアスを減らせる
二重盲検化(Double Blinding)
・最も望ましい
・被験者/治験責任者(被験者評価を担当する医師)/治験依頼者(製薬会社)の三者全てが、被験者に割り付けられた試験治療(投与薬剤)を知れないようにすること
・被験者(患者)がプラセボ対象だと知ると、効果があるわけがないと健康に気を使わなくなる(逆に実薬対象だと知ると、効果を期待して無意識に健康に気を使うようになる)
・治験者(医師)が実薬対象だと知ると、何かしらの効果や副作用があるはずだと関連付けてしまう
・依頼者(製薬会社)が実薬対象だと知ると、解析手法を有利な結果が出るように変えてしまう
V さまざまな検定を理解する
検定結果を理解する際のポイント
帰無仮説と対立仮説を読む
・どの統計量に対する検定なのか判る(例:t検定なら母平均)
検定を選択する際のポイント
①対応の有無:同一のサンプル群から得られたデータか?
②アウトカム:連続データ/カテゴリカルデータ/生存時間データ、など
③正規性:母集団が正規分布に従っていると見做せるか?
④群の数:新薬群(高用量)/新薬群(低容量)/プラセボ群なら3群
t検定
・連続データに対する検定
・パラメトリック検定(正規分布)なので、正規分布に従っていない場合は有意差を出しにくい→Wilcoxon順位和検定を使うのがbetter
帰無仮説H0:A群の母平均=B群の母平均
これを棄却できた(有意差が出た)場合、
対立仮説H1:A群の母平均≠B群の母平均
が主張できる
しかし、棄却できなかった場合、
「A群の母平均=B群の母平均」と主張することはできない
主張できるのは、『「A群の母平均≠B群の母平均」とは言えない』ということのみ
t検定の手順
①t統計量を算出する
②t分布を参照してP値を算出する
③P値と有意水準を比較する
Wilcoxon順位和検定
・連続データに対する検定
・ノンパラメトリック検定(母集団の分布を仮定しない検定)なので、正規分布に従っている場合はt検定の方が有意差を出しやすい
・Mann-WhitneyのU検定と実質的に同じ(名称が違うだけ)
分散分析(ANOVA、ANalysis Of VAriance)
・3群以上の母平均に関する検定(目的はt検定と同じ、3群以上の場合はt検定が使えないため分散分析を使う)
・分散を使って母平均を検定しているので、「分散分析」と呼ばれている(分散を検定しているわけではないので要注意)
・分散分析で有意差が出ても、「3群のうち、いずれかの2群間で差がある」ことしか主張できない
・しかし、分散分析の後で2群のt検定を行うことは、「多重性の問題」を引き起こすため、推奨されない
・一元配置ANOVA:1個の因子の影響による、水準間の母平均の差を解析したい場合(例:血液型4種による母平均の差)
・二元配置ANOVA:2個の因子の影響による、水準間の母平均の差を解析したい場合(例:血液型4種×性別2種の組み合わせ=8水準による母平均の差)
分散分析表の見方
・一般的に、F値が大きいとP値が小さくなる(いずれかの群間に差がある可能性が高くなる)
F検定(等分散性の検定)
分割表に関する検定①:ピアソンχ二乗検定(独立性検定)
・この「独立性」とは、「2変数間で関連がないこと」
・例えば、「薬剤投与の有/無」と「回復の有/無」
ステップ
①期待度数を算出して分割表を作成する
②観測値と期待度数の差を算出する
③χ二乗値を算出する
④自由度を算出する
⑤χ二乗分布表を参照してP値を算出する
分割表に関する検定②:Fisher直接確率検定(正確検定)
やっていることはχ二乗検定と同じ
違うのは、P値の算出方法だけ
・χ二乗検定では、P値を算出するために近似値(χ二乗値)を使うため、データ数が少ないと精度が悪くなる(算出したP値の信頼性が落ちる)
・Fisher直接確率検定では、直接的にP値(確率)を計算するため、データ数が少なくても精度が高い(具体的には、分割表のセルが1つでも5以下であれば、Fisher直接確率検定を使うべき)
補足:2種のピアソンχ二乗検定
ピアソンχ二乗検定は、カテゴリによって2種類に区別される
・適合度検定:カテゴリは1つ(理論値 vs. 測定値)
・独立性検定:カテゴリが2つ(例:「投薬する/しない」と「発症する/しない」)
帰無仮説を比較すると、
・適合度検定のH0:測定値は理論値に従う
・独立性検定のH0:「投薬の有無」と「発症の有無」は独立である
検定の流れを比較すると、
①データをクロス集計表にまとめる
②
・適合度検定:理論値(比率)を決める
・独立性検定:「2群の差がない」と仮定した場合の理論値(比率)を算出
③理論値と実測値とのズレを計算
④カイ二乗分布を使って理論値とのズレが偶然である確率(p値)を算出
⑤p値が有意水準より小さければある群とある群に差があると判断
VI 多重性とはなにか
統計的検定を複数回実施すると、少なくとも1つの検定について、有意になる確率が増大してしまう問題
本当は差がないのに、誤って有意差があると結論づけてしまう(αエラー)
多重性を回避する方法
①検定を1回きりにする
②検定に順番を付ける(閉手順にする):検定をAND条件にする
③有意水準を小さくする:Bonfferroni法(検定1回の場合は有意水準α=5%なので、検定を2回にするなら各回2.5%、5回にするなら各回1%にする)
VII 生存時間解析
がん領域の製薬で使われることが多かったため、「生存時間」と呼ばれている
生存/死亡データ以外にも適用できる
生存時間データと連続データの違い(t検定やWilcoxon順位和検定を適用しない理由)
①生存時間データは「イベントが発生するまでの時間」を扱うため:イベントとは、一度きりしか起こらない事象(例:死亡、故障、離職、解約)
②「打ち切り」を考慮できるため:試験期間中にイベントが発生しない場合を区別できる
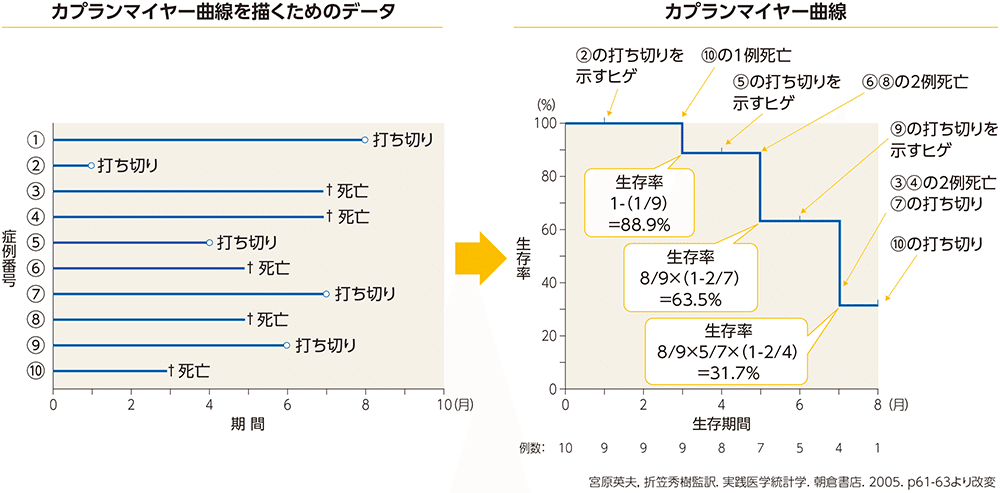
Kaplan-Meier曲線
生存時間解析のデータを可視化したもの
(「イベント」と「打ち切り」がどの時点で発生したかを可視化したもの)
・縦軸:イベント未発生の個体の割合
・横軸:時間
VIII 回帰分析・共分散分析
2個のフィールド(例:身長、体重)を持つデータを手に入れたらどんな解析をするか?
①各フィールドの要約統計量を算出してみる
②各フィールドのヒストグラムを作成して可視化してみる
③散布図を描いてみる
④回帰分析や相関を算出してみる
回帰分析
Y = a*X + b + 誤差
・Y:応答変数
・a:係数
・X:説明変数
・b:切片
共分散分析(ANCOVA、ANalysis of CO-VAriance)
・分散分析(ANOVA)に回帰分析を応用したもの
・共変量(平均値に影響を及ぼすデータ)の影響を取り除いて、3群以上の群間比較を行える
・交絡因子:交絡バイアスを引き起こす因子
・共変量:共分散分析で調整する説明変数(特に連続変数である場合)
そのため、交絡因子を共分散分析で調整するのであれば、その因子は交絡因子であり、かつ、共変量です。
ですが、交絡因子であっても共分散分析で調整しないのであれば、共変量ではない、ということになります。
例:2社の平均年収の比較
・単に平均年収について分散分析をしただけでは、例えば年齢が年収にどう影響しているか判らない
・年齢を共変量として共分散分析を行うと、平均年収×年齢上の回帰直線を比較することができるため、特定年齢における平均年収を比較することができる
IX 相関
相関と回帰分析の違い
・相関:2変数の散らばり傾向のみを見ている、xとyを交換しても相関係数r(ピアソン積率相関係数)の値は変わらない
・回帰分析:説明変数xから応答変数yを予測するために使う
相関に関する検定
「相関係数が大きい」ということと、「相関係数の検定が有意」ということは全く別の問題
無相関検定(相関係数の検定)
・帰無仮説H0:相関係数=0
・対立仮説H1:相関係数≠0
つまり、H0が棄却できたとしても、主張できるのは「相関係数≠0」のみ
P値は相関係数の大小だけではなく、データ数にも依存するため、P値だけを見て(有意差があるかどうかだけを見て)、相関係数の高低に言及することはできない
・相関係数が0.1(低相関)でも、P<5%(有意)の場合もあるし、
・相関係数が0.8(高相関)でも、P>5%(有意ではない)の場合もある
完
補足
なし
分類性能
混同行列(Confusion Matrix)
混同行列(クロス集計表の一種)情報から、分類性能に関する様々な指標を算出できる
※医療統計における所謂「検査の精度」は、統計学的には「分類器の性能」を意味する
感度と特異度(高い方が良い)
※「疾患がない」を帰無仮説とした場合
感度(Sensitivity)
・疾患がある人を正しく検出する力
・定義式:感度=陽性+と判定された人/疾患がある人
・同義語:感度(sensitivity)、再現率(recall)、真陽性率(TPR、True Positive Rate)
特異度(Specificity)
・疾患がない人を正しく検出する力
・定義式:特異度=陰性-と判定された人/疾患がない人
・同義語:真陰性率(TNR、True Negative Rate)
・感度(真陽性率、再現率)が高い検査(陽性が出やすい検査)は、除外診断(スクリーニング)に向く
・特異度(真陰性率)が高い検査(陽性が出にくい検査)は、確定診断に向く
つまり、実際の病気の診断においては、以下のアプローチをとる
・まず、感度の高い検査(たとえば便潜血:大腸癌で陽性になりやすいが、痔など他の腸疾患でも陽性となる、など)でスクリーニングを行い
・次に、怪しいと判断された被験者に対し特異度の高い検査(たとえば内視鏡:大腸癌を視認しないと陽性にならない、など)を行って確定診断する
偽陽性率と偽陰性率(低い方が良い)
偽陽性率(FPR)
・定義式:1-特異度
・疾患がないのに誤って「陽性+」と判定されてしまう割合
・同義語:偽陽性率(False Positive Rate)、第1種過誤(Type1 Error)、α過誤(あわて者の誤り)、過検知
偽陰性率(FNR)
・定義式:1-感度
・疾患があるのに誤って「陰性-」と判定(看過)されてしまう割合
・同義語:偽陰性率(False Negative Rate)、第2種過誤(Type2 Error)、β過誤(ぼんやり者の誤り)、検知漏れ(看過)
検査の感度(真陽性率TPR)を高めようとすると、同時に偽陽性率FPRも上がってしまうというトレードオフ関係がある
トレードオフを考慮して性能を評価する方法が、ROC曲線である
陽性的中率と陰性的中率(高い方が良い)
感度/特異度と偽陽性率/偽陰性率の分母は、疾患のある人/ない人の数
それに対して、
陽性的中率/陰性的中率(Predictive Value)の分母は、陽性/陰性の人の数
この違いにより、PPV/NPVには、有病率の影響を受けやすいという性質がある
陽性的中率(PPV)
・定義式:PPV=実際に疾患がある人/陽性+と判定された人
・同義語:陽性的中率、適合度(Precision)、精度
陰性的中率(NPV)
・定義式:NPV=実際に疾患がない人/陰性-と判定された人
・同義語:陽性的中率、適合度(Precision)、精度
検査の感度(真陽性率TPR、再現率Recall)を高めようとすると、同時に適合率Presicionが下がってしまうというトレードオフ関係がある
トレードオフを考慮して性能を評価する方法が、PR曲線である
F値
適合率Presicionと再現率Recallの調和平均
陽性尤度比と陰性尤度比
英:Positive/Negative Likelihood Ratio
陽性尤度比が高く、陰性尤度比が低いとき、良い検査であることを意味します。
性質
陽性尤度比/陰性尤度比は、検査の結果を見た後に被検者が実際に病気である確率(=検査後確率)を求めるために使用されます。
検査前確率
「検査をする前に被験者が病気である確率」を検査前確率といいます。
これは有病率に等しくなります。
有病率(Prevalence)
・検査を受けた全員のうち、実際に陽性であるべき人の割合
・定義式:有病率=(TP+FN)/全員
検査自体は同じでも、有病率によって正確度や適合度は変わる
疾患の深刻度などにも応じて、各種指標のバランスのよい検査が求められる
正確度(Accuracy)
・正しく検出する力(疾患の有無は無関係)
・定義式:正確度=(TP+TN)/全員
・同義語:正確度(Accuracy)、正解率
AUC評価(ROC曲線とPR曲線)
悪魔の証明(非存在の直接証明)の困難性
科学の分野では、悪魔の証明は仮説の否定が困難である場合に問題となる。例えば、「ある物質が人体に有害である」という仮説が立てられた場合、その物質が無害であることを証明することは難しい(無限に想定し得るあらゆる条件下で、その物質の有害性が存在しないことを証明する必要があるため)。このような場合、科学者は帰無仮説(「ある物質は人体に有害ではない」)を立て、実験や観察によって有害性を示す証拠を集めることにより、帰無仮説を棄却して「ある物質が人体に有害である」という対立仮説を採択しようとする。
悪魔の証明は、日常生活や議論の中でも問題となることがある。例えば、ある人が他人に対して悪意を持っているという主張がなされた場合、その人が悪意を持っていないことを証明することは困難である。このような場合、悪魔の証明を避けるためには、主張を立証する責任を持つ者が具体的な証拠を示すことが求められる。
論理的にも、非存在を証明するためには、その対象がどこにも存在しないという全称的な主張を立証する必要がある。これに対する反例が一つでも見つかれば、その主張は簡単に崩れる。このため、非存在の証明は論理的に非常に脆弱である。
「効かないことの証明」が難しい3つの理由
医学領域において「効かないこと」を直接的に示すのが困難である理由としては,以下の3点が挙げられます。
①統計学的仮説検定の手続き上、「効かないこと」の直接証明は難しい(検定の結果が「有意差なし」となっても帰無仮説「効かない」を採択することはできない)
②無益性を示すための試験は倫理的に不可能
③「あなた個人の未来は誰にも分からない」問題
