
Pythonを使ってキャビネットIRの波形と周波数特性を見てみよう
要旨
Pythonを用いて、キャビネットIRの周波数特性を求めます。
導入
お久しぶりです。大学院試験に受かり、来春から大学院生です。学部で必要な単位はあと卒業研究だけなので、多分卒業できます。
研究室にいると音楽や機材製作に対するモチベーションが湧きにくいですが、軽音サークルの人と連んでいるとモチベーションが湧いてきますね。このネタも半月くらい暖めていましたが、久しぶりに長い時間話してたら何かしら機材関係でアウトプットしたくなってきたので、帰宅して熱が冷めないうちに一気呵成していきます。
動機
さて、本題ですが、Pythonを使って手持ちのIRデータの波形を周波数特性を抽出します。動機としては、わざわざIRをマルチエフェクターにロードして試奏せずとも傾向を掴みたいことに加え、好きなIRの周波数特性を把握することで、IR探しや音作りの役に立つのではないかと考えたからです。
そもそもIRとは?
キャビネットIRは、アンプのキャビネットから出力され、マイクで拾った音を再現するために用いる短い音声データを指します。
IRはImpulse Responseの略で、(一部)日本語に訳すとインパルス応答といいます。インパルスとは、要するにパルス信号のことで、身近な例だと風船の割れる音がそれに近いです。人によってはデルタ関数と言った方が伝わるかもしれません。実際に、キャビネットIRの入ったwavファイルを再生してみると、パツン!という音が聴けます。
ここで重要なことは、パルス信号(デルタ関数)を基準の信号とするということです。突然ですがデルタ関数をフーリエ変換(周波数分解)するとどうなるでしょうか?その答えは以下のサイトの『フーリエ変換』項にあります。
デルタ関数のフーリエ変換は1という定数関数になることが示されています。このことはつまり、『パルス信号には全ての周波数成分が一様に含んでいる』ことを表しています。このことが非常に重要で、『理想的なパルス信号で構成されるIRに信号を通したとしても、出力される音に全く変化はない』ということが言えます。これはフラットなEQを通した音、と同じことです。
キャビネットIRはこのパルス信号を加工して、周波数成分を調整したものです。要するに調整済みEQです。もし仮に十分細かく調整できるEQがあれば、IRの音は全く再現可能です。
IRとは調整済みEQである、ということは以下の二つの特性を併せ持つことも同時に示しています。一つ目は、歪みの情報を持たないこと。二つ目は、どんな音量に対しても特性は同じ、ということです。これらの特性は現実のキャビネットやマイクの特性と乖離を生む要因となっていますが、ここでは深入りしないことにします。(3Blue1BrownJapan風)
コード
仕様について簡単にまとめると、 指定したフォルダのパスに入れたIRデータを全て読み込んで、グラフにプロットしていく流れになります。
表示するグラフは①IRデータの生波形、②FFT結果の二つです。ファイルの数だけプロットされます。
オマケ仕様として、コード末尾のplotter.plot(mode='XX')のXXの部分にadjustedと入力すると、波形のピーク位置が揃ったグラフが描画されます。ピーク位置が異なる波形同士の比較をする際はこちらを設定するといいです。
Pythonは始めたてということで全く詳しくないので、内容の解説は省略しますが、コメントを読めばある程度の改造はできると思います。
実行環境がある方はこれをコピペしてフォルダパスを指定するだけで使えますし、実行環境なんて無いよ!!という方は後述のGoogle Colabを用いる方法を使うと簡単に実行できます。
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as wavfile
import os
from matplotlib.ticker import EngFormatter, MultipleLocator
class ImpulseResponsePlotter:
def __init__(self, original_data, adjusted_data, rates, time_axes, file_names):
self.original_data = original_data
self.adjusted_data = adjusted_data
self.rates = rates
self.time_axes = time_axes
self.file_names = file_names
def plot(self, mode='original'): # modeを追加して波形の種類を選択
fig, axs = plt.subplots(2, 1, figsize=(15, 8))
self._plot_waveform(axs[0], mode)
self._plot_fft(axs[1])
plt.tight_layout()
plt.show()
def _plot_waveform(self, ax, mode): # 波形プロット(originalまたはadjustedを選択)
if mode == 'original':
data_set = self.original_data
title = 'Impulse Responses (Original)'
elif mode == 'adjusted':
data_set = self.adjusted_data
title = 'Impulse Responses (Adjusted)'
else:
raise ValueError("Invalid mode. Choose 'original' or 'adjusted'.")
ax.set_title(title) # タイトル
ax.set_xlabel('Time (ms)') # x軸ラベル
ax.set_ylabel('Amplitude (Normalized)') # y軸ラベル
ax.set_xlim(0, 5) # x軸の表示範囲の設定
ax.set_xticks(np.arange(0, 10.1, step=1)) # x軸の目盛り
ax.set_yticks(np.arange(-1, 1.1, step=0.5)) # y軸の目盛り
ax.xaxis.set_minor_locator(MultipleLocator(0.1)) # サブグリッド(x軸)
ax.yaxis.set_minor_locator(MultipleLocator(0.1)) # サブグリッド(y軸)
ax.grid(True, which='major', linestyle='-') # メジャーグリッド線
ax.grid(True, which='minor', linestyle=':') # マイナーグリッド線
for i, data in enumerate(data_set): # 選択されたデータのプロット
ax.plot(self.time_axes[i], data, label=self.file_names[i])
ax.legend(bbox_to_anchor=(1.02, 1), loc='upper left', fontsize='small') # 凡例の設定
def _plot_fft(self, ax): # インパルス応答のFFTプロット
# グラフにプロットする周波数範囲
min_freq = 20 # 最小周波数
max_freq = 20000 # 最大周波数
ax.set_title('FFT of Impulse Responses') # タイトル
ax.set_xlabel('Frequency (Hz)') # x軸ラベル
ax.set_ylabel('Magnitude (dB)') # y軸ラベル
ax.set_xscale('log') # x軸を対数スケールに設定
ax.set_xticks([min_freq, 50, 100, 500, 1000, 5000, 10000, max_freq]) # 対数スケール用の目盛り
ax.set_xlim(min_freq, max_freq) # x軸の表示範囲の設定
ax.set_ylim(-60, 5) # y軸の表示範囲の設定
ax.grid(True, which='both', linestyle='-') # メジャー&マイナーグリッド線
formatter = EngFormatter(unit='', sep='') # 工学形式のフォーマッタ
ax.xaxis.set_major_formatter(formatter) # x軸フォーマットの設定
# FFTを実行しグラフにプロット
for i, data in enumerate(self.original_data):
N = len(data)
fft_result = np.fft.fft(data)
freqs = np.fft.fftfreq(N, 1 / self.rates[i])[:N // 2]
fft_magnitude = np.abs(fft_result)[:N // 2] # 絶対値を取得
# 指定周波数範囲内のインデックスを取得
valid_indices = np.logical_and(freqs >= min_freq, freqs <= max_freq)
max_in_range = np.max(fft_magnitude[valid_indices]) # 周波数範囲内の最大値で正規化
fft_magnitude_db = 20 * np.log10(fft_magnitude / max_in_range) # デシベル変換
ax.plot(freqs, fft_magnitude_db, label=self.file_names[i]) # データのプロット
ax.legend(bbox_to_anchor=(1.02, 1), loc='upper left', fontsize='small') # 凡例の設定
# データを保持するリスト
original_data = []
adjusted_data = []
rates = []
time_axes = []
peak_positions = []
file_name_x = []
# 対象のフォルダ
folder_path = '/Users/~/' #任意のフォルダパスを設定する
# フォルダ内のすべてのWAVファイルを処理
for file_name in os.listdir(folder_path):
if file_name.endswith('.wav'):
file_path = os.path.join(folder_path, file_name)
rate, data = wavfile.read(file_path)
if data.ndim > 1: #ステレオの場合、片方のチャンネルを取得
data = data[:, 0]
data = data / np.max(np.abs(data)) # データの規格化
time_axis = np.arange(len(data)) / rate * 1000 #時間軸をmsに
#ピーク位置を合わせるためのデータを取得
peak_index = np.argmax(data)
peak_time = time_axis[peak_index]
original_data.append(data)
rates.append(rate)
time_axes.append(time_axis)
peak_positions.append(peak_time)
file_name_x.append(file_name)
# 基準となる最速のピーク位置を取得
min_peak_time = min(peak_positions)
# 時間軸を調整
for i, data in enumerate(original_data):
shift_ms = peak_positions[i] - min_peak_time
shift_samples = int(shift_ms * rates[i] / 1000)
adjusted = np.roll(data, -shift_samples)
adjusted_data.append(adjusted)
# 描画
plotter = ImpulseResponsePlotter(original_data, adjusted_data, rates, time_axes, file_name_x)
plotter.plot(mode='original') # 'original' または 'adjusted' を指定 以下のサイトを参考にしつつ、ChatGPTに投げまくりながら作りました。多分100回弱くらいやりとりしています。
ChatGPTを使うと実力が育たない!とか言われますが、まあコードを書くのが仕事ではないのでいいでしょう。
ちなみに研究ではExcelのグラフのフォーマットを統一するためのVBAを書かせてますが、地味に便利なのでおすすめです。色とか、フォントサイズとか、一々調整するのは面倒ですからね。
出力例
実行してみるとこんな感じのグラフが表示されます。
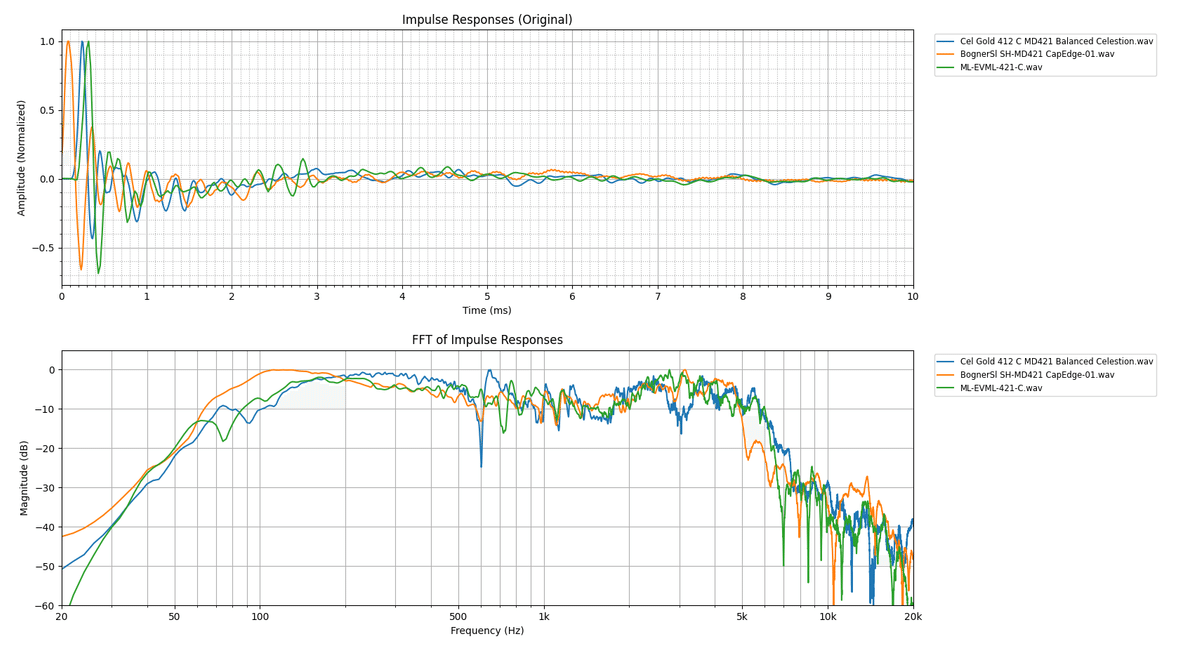
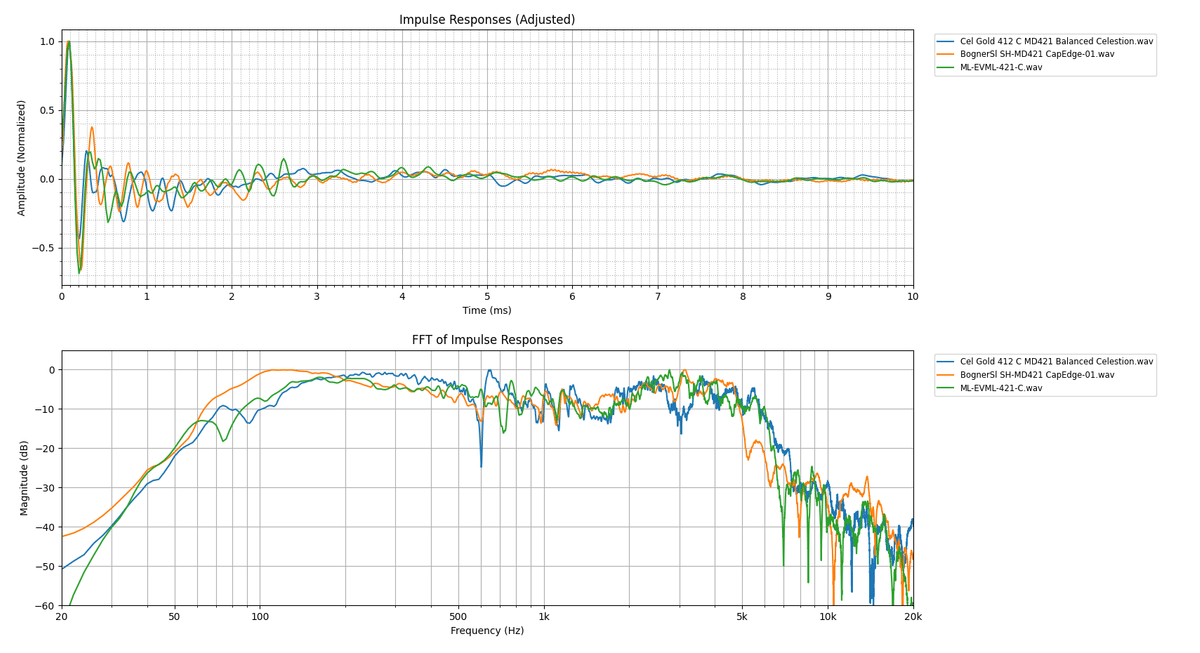
コードの章でも説明しましたが、一番上がwavファイルの規格化した波形、二番目が周波数特性です。是非拡大してご覧ください。
Google Colabを使って実行する
実行環境がない方向けにGoogle Colabを用いた利用方法を紹介していきます。
まず、以下のサイトにアクセスしてください。上記のコードとほぼ同じ内容があります。
次に、ご自身のGoogleアカウントでログインして、左上の『ファイル』→『ドライブにコピーを保存』を選択してください。そうすると、ファイル名が『IR_FFT.ipynbのコピー』となるので、これで第一段階は完成です。

第二段階として、IRをインポートするためのフォルダを作成していきます。先ほどログインしたアカウントでGoogleドライブを開いてください。
左のマイドライブを選択してから左上の『+ 新規』を選択し、新しいフォルダを作成します。フォルダ名は写真のように『IR』としてください。

そして、そのフォルダの中に、解析したいIRファイルをいくつか入れてください。これでGoogleドライブでの操作は完了です。
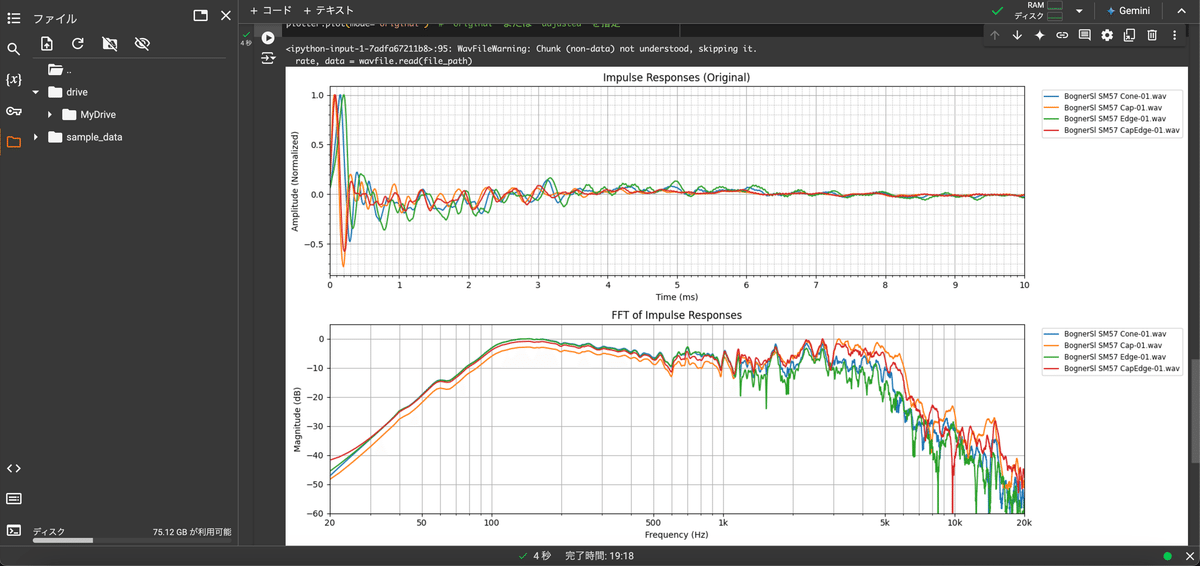
最後にもう一度、『IR_FFT.ipynbのコピー』を開き、左端にあるフォルダのアイコンをクリックすると『ファイル』という領域が開くので、下写真の赤丸部分『ドライブをマウント』を選択します。そうすると、色々操作が要求されるので、許可してください。

そうすると、MyDriveが表示され、IRのフォルダとその中身が確認できるようになります。

この状態になれば実行可能です。▶ボタンを押して実行すると、結果が下に表示されるはずです。
遊んでみた
Celestion系
まずは手持ちのCelestionのキャビネットを比較します。アルニコ系(+Vintage30)とそれ以外に分けています。A-typeだけオープンバックです。マイクやチューニングの条件は揃えています。

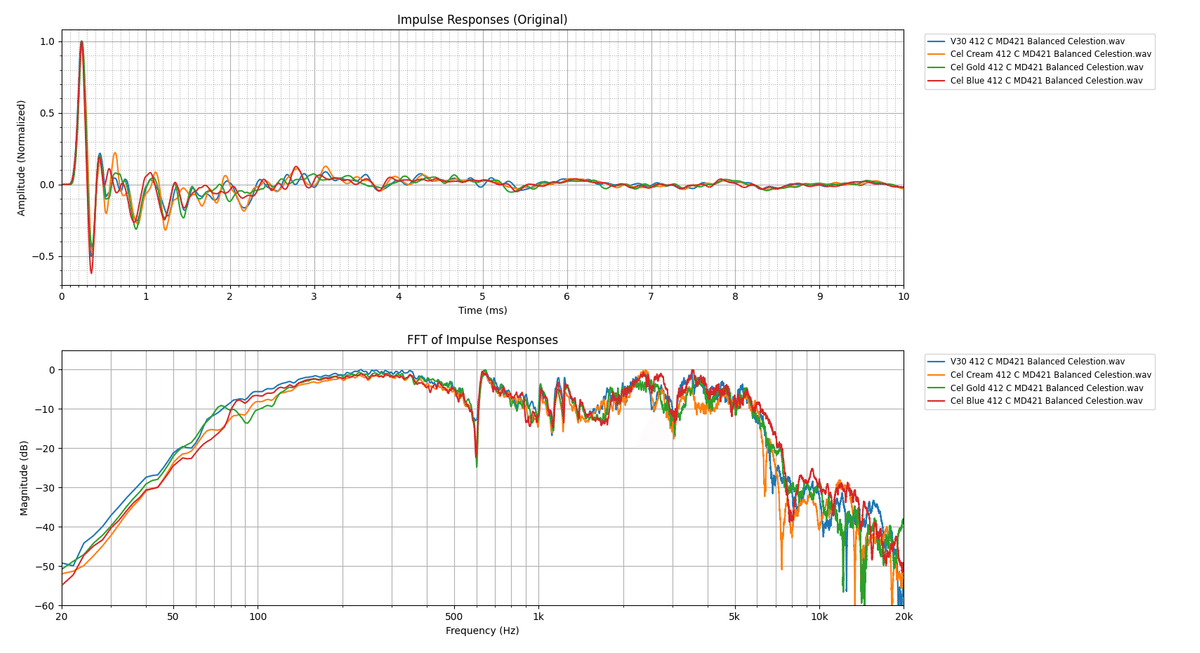
やはり、アルニコ系は似たような傾向を示しますね。A-type以外は割と似たり寄ったりですが、これは明らかに私の好みが影響してますね…
一つ特徴的な傾向として、クローズドバックのキャビネットでは600Hzでシャープな谷が形成されています。キャビネットのサイズは違いますが、Goldは212オープンと412クローズの2種類を持っているので、波形を比較してみます。マイク依存性を排除するため、Royer R-121のIRデータも示しています。

やはり600Hzに特徴的な谷が見られますね。
何故600Hzだけ凹んでしまうのかは計算からも説明することができて、600 Hzの波長$${\lambda\,\mathrm{[m]}}$$は
$$
\begin{equation} \begin{split}
\lambda &=\frac{1}{f\,\mathrm{[Hz]}}\times v\,\mathrm{[m/s]} \\ &=\frac{1}{600\,\mathrm{Hz}}\times340\,\mathrm{m/s} \approx 0.57\,\mathrm{m}
\end{split} \end{equation}
$$
音波は固定端反射ですから、反射波の位相が$${\pi}$$変化することを考慮すると入射波と反射波が互いに弱め合う節となる条件$${l_{node}\,\mathrm{[m]}}$$は
$$
l_{node}=N\times\frac{\lambda}{2}\approx0.28N\,\mathrm{[m]}\,\,(N\in\mathbb{N)}
$$
となり、600HzがN=1条件とすると、スピーカーユニットの端⇔キャビネット内壁の距離が30cm程度となることが分かりますね。一般的なキャビネットの奥行き(外寸)が40cm弱であることを考慮するとそれが原因であると考察できます。
https://www.soundhouse.co.jp/products/detail/item/52232/
https://www.soundhouse.co.jp/products/detail/item/88526/
オープン・クローズドの話はここら辺にしておいて、次はマイクによってどのように特性が変化していくか見ていきましょう。
CelestionのキャビネットIRでは基本的にSennheiserのMD 421とSHUREのSM57、RoyerのR-121でキャプチャしたIRデータがバンドルされています(ルームマイクを除いて)。R-121だけリボンマイクで他はダイナミックですね。リボンの121とダイナミックをミックスして使うことを想定していると思われます。

リボンマイクはやはり低域が持ち上がった特性になりますね。これはイメージ通りですし、実際使ってみるとかなり暗い音に感じます。
対してダイナミックマイクのMD421とSM57はかなり似ているように感じますね。もう少し細かく特性を見たいのでコードを弄って差分を求めてみました。(コードはおまけ項にあります)

この結果を見るに、MD 421の方が中低域が強いと言えそうですね。IRや実機で比較したことある多くの方もそういった印象を持たれていると思います。 SM57は5~10kの高音部分が顕著に強いですから抜け感のある音を作りやすい印象です。
次に、同一マイクのチューニング違いを見ていきます。Celestionの各マイクには
Balanced
Bright
Dark
Dark2
Fat
Thin
の6種類がバンドルされています。なので3種類のマイク$${\times}$$6種類のキャラクターで計18種類、それに加えて、ルームマイクサウンドが3種類、ミックスされたファイルが12種類くらいありますから、1つのキャビを買うだけで結構楽しめます。今回はMD421で見ていきます。

全部ひとまとめにするとわかりにくいので半分ずつプロットしてみます。また、わかりやすいようにFFT結果のy軸の範囲を-40から5dBにしています。
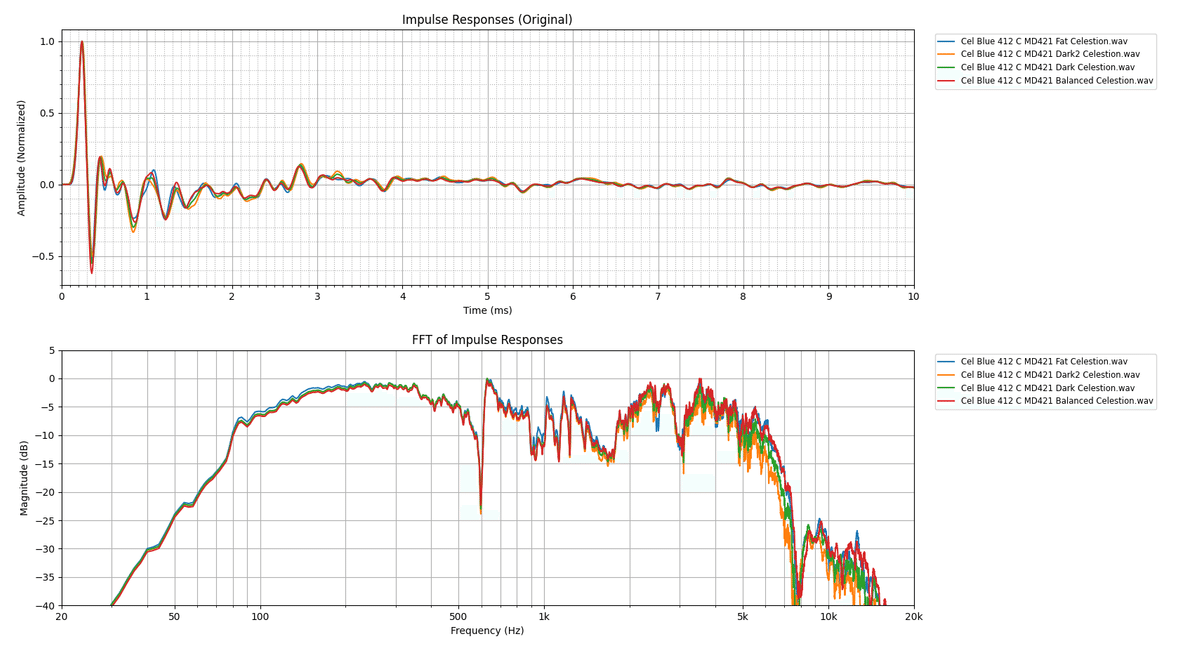
BalancedとFatはそこまで大きな違いはないですね。やや低域と中域が持ち上がっている程度でしょうか。Darkは結構高音域が削れています。1よりも2の方が削れ方が大きいです。
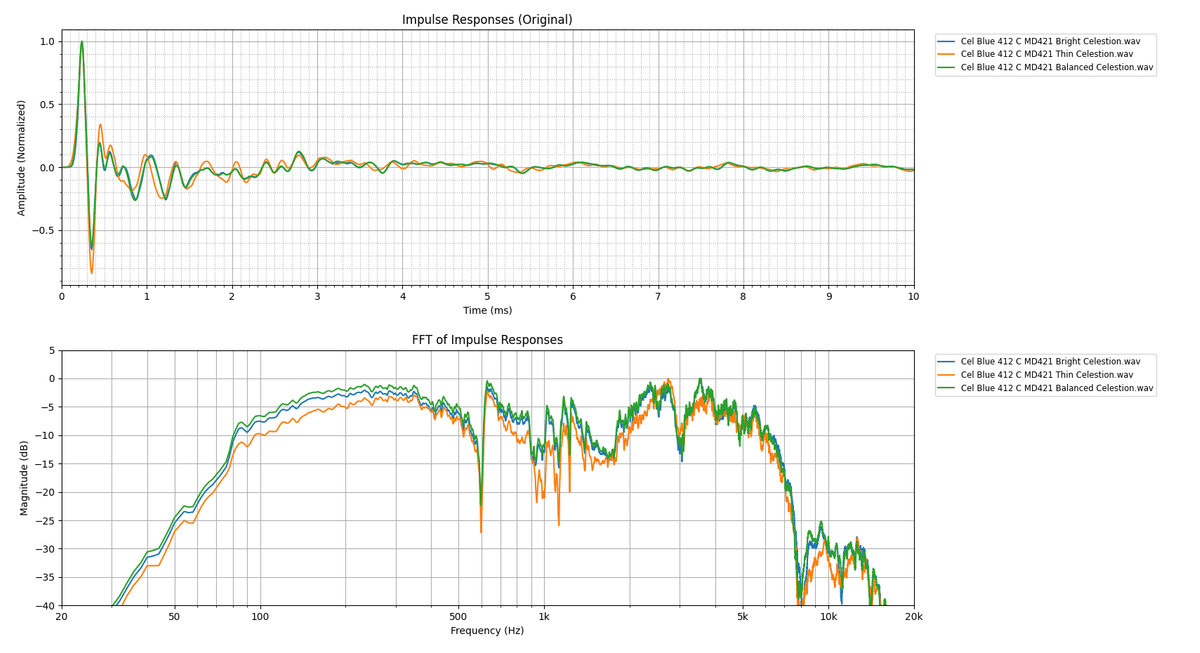
Thinは結構Balancedから離れていますね。また、EQで補正した感じではなく、マイキングが他のキャラクターのものとは違ってそうですね。BrightはBalancedから中低音を調整したような特性です。
縦軸の幅が大きいためあまり違いが無いように見えますが、3,4dB変わっただけでも音質には大きな影響がありますから、かなり印象は変わってきます。これらの傾向を頭に入れながら音作りやIR作りをするのがいいと思います。
DYNAX IR
DYNAXは日本でIRを作製しているメーカーです。「独自の手法」を用いてリアルなサウンドを追求しているとのことです。
DYNAXのいいところは扱っているキャビネットの種類が多いことと、1つのパッケージに含まれるサウンドの数は100種類以上とボリューミーなことです(私が所有しているBognerキャビは102種類でした)。使われているマイクも20種類くらいあります。
では、私の所有しているBogner 412SL SlantのIRモデリングについて一部見ていきましょう。ちなみにスピーカーはVintage 30みたいです。
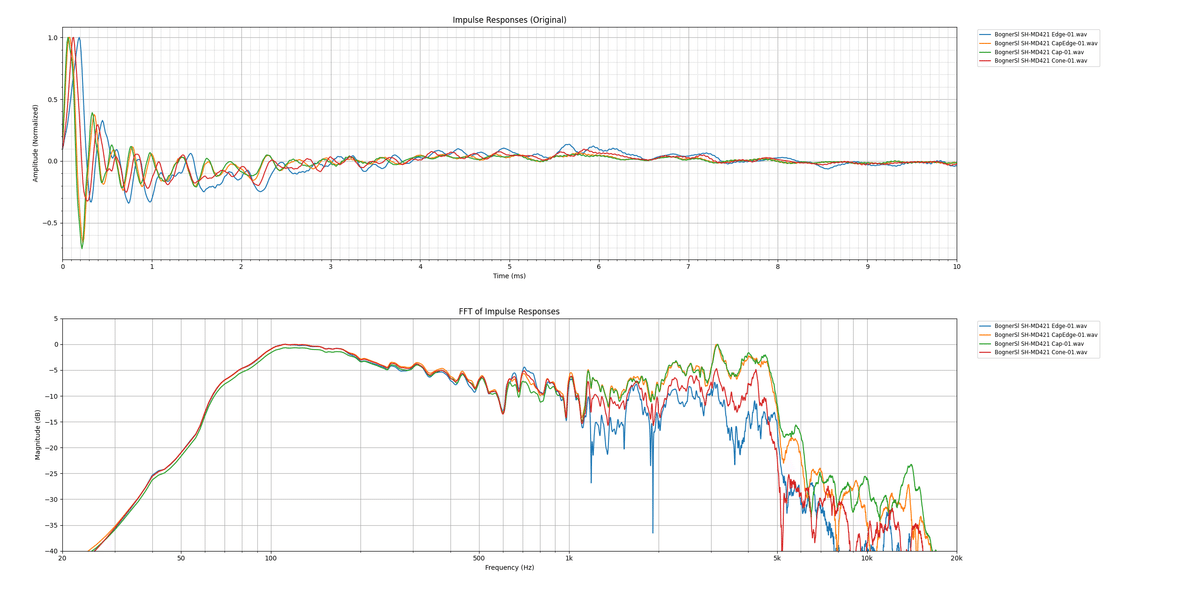
波形を見てみてると、Celestionよりレスポンスが速いです。恐らく、タッチレスポンスを良くするために調整しているのだと思います。0.何msecの差なので認識するのは難しいですが、もしかすると、音が良く感じる一因になっているのかもしれません。
また、Celestionとは違い、マイキングの位置がファイル名となっています。なので、マイキングの勉強にも役立つと思います。一般論としてCapに近いほどブライト、コーンに寄れば寄るほど暗い音、といわれてますし、実際そのような傾向になっていることが分かるかと思います。
次に、マイク違いを見ていこうと思います。収録されているマイク全部を投げるとこうなりますが、訳わかんないのでとりあえずいくつかピックアップしてみます。
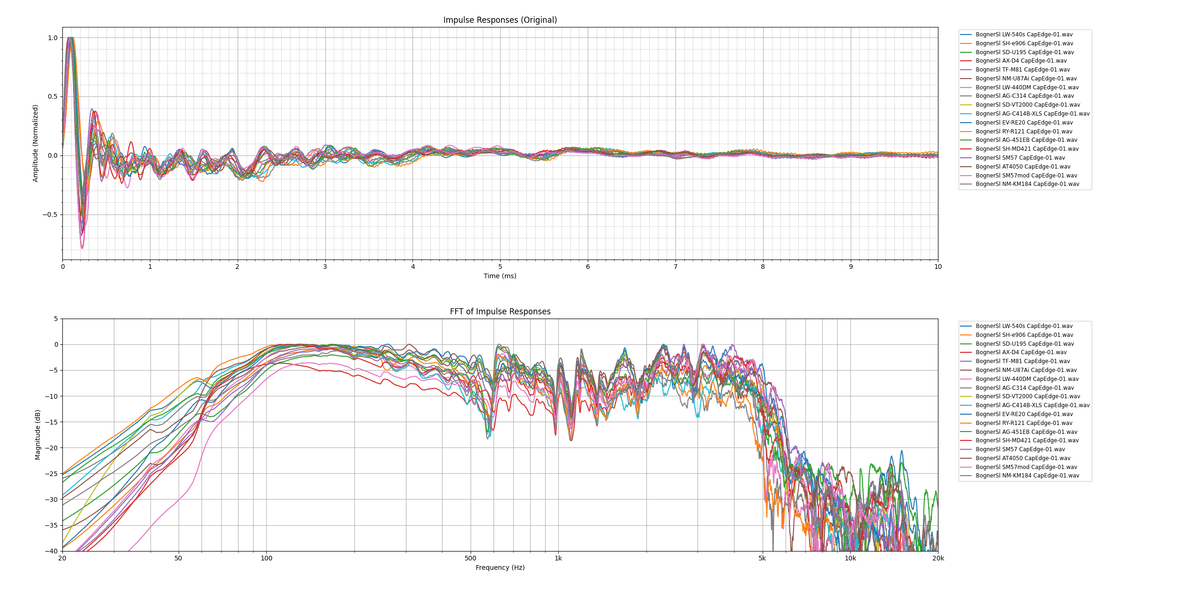

とりあえず、構造別に代表的な機種をピックアップしてみました
Sennheiser MD 421 / ダイナミック(単一指向性)
TELEFUNKEN M81 / ダイナミック(超単一指向性)
NEUMANN U 87 Ai / コンデンサ(ラージダイアフラム)
AKG C451EB / コンデンサ(スモールダイアフラム)
Royer R121 /リボン
こうしてみると、特徴をよく抑えてる特性になっていると思います。
低域が豊かなリボン、4k5kが強いダイナミック、レンジの広いスモールダイアフラムと、バランス型のラージダイアフラムと使い分けると一歩進んだ音作りが出来ますね。
個人的に一番好きなIR
私自身10種類くらいしかIRを持っておらず、オタクの中では少ない方かもしれませんが、個人的に今一番気に入っているIRがあります。それはいままで紹介したCelestionやDYNAXではなく、ML Sound labから出ているEVML Classic Cab Packです。ステマではありません。
これを買った経緯としては、どうしてもElectro VoiceのEVM-12LのキャビIRが欲しくて探してたら見つけた、というシンプルな理由です。EVM-12Lはダンブルアンプの一部に採用されていたらしく、UAFXのDreamやEnigmaticにもキャビシミュとして収録されています。
音の傾向としてはアルニコ系らしくかなりブライトですが、Celestionのアルニコ系よりもミッドのバランスがいいと感じて扱いやすいです。下によく使う3種類をピックアップしましたが、その中でもよく使うのはRoyer R-121のCapと思われるもので、かなりドンシャリ気味であり、モデリングアンプの歪みとの相性が抜群に優れてますし、かなりユニークな音ですが扱いやすいです。
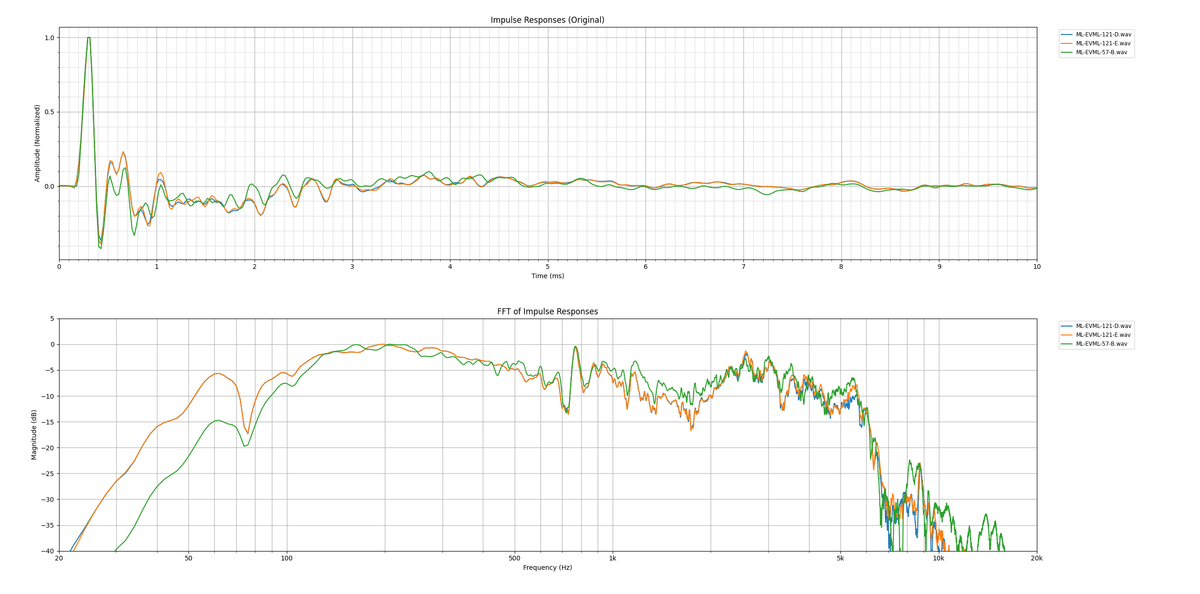

他のIRとの比較を見てもらえば分かり易いですが、アルニコ特有のレンジの広さもありつつ、ミッドもしっかり出ていることが分かると思います。特に5,6k辺り特有のギラギラ感がたまりません。
GT-1000やGX-100系を持っている方は試して欲しいのですが、EVM-12LとX-CRUNCHプリアンプの相性は最高です。私自身、周りの人間に布教しまくっている組み合わせです。個性と音の良さを両立出来る最強の組み合わせだと思っています。
最後に
この時点で11,000字に到達しています(コード込みなので実際の文字数はこれよりも少ない)。卒論もこれくらいの勢いで書きたいものです。
買うと意外と高いIRの分析用ソフトをPythonでChatGPTを活用しながら作ってみました。プログラミングの知識が無くても、結構簡単にできるので改造など是非チャレンジしてみてください。
あと、リバーブIRを分析するとなると、時間軸方向のプロットも必要になります。つまり3次元プロットです。大変です。頑張ってみます。
おまけ
周波数特性の差を見るコード
フォルダ内に2つ以上IRファイルがあるとエラーになるので注意してください。
import numpy as np
import matplotlib.pyplot as plt
import scipy.io.wavfile as wavfile
import os
from matplotlib.ticker import EngFormatter, MultipleLocator
class FFTDifferencePlotter:
def __init__(self, original_data, rates, file_names):
self.original_data = original_data
self.rates = rates
self.file_names = file_names
@staticmethod
def smooth(data, window_size=5):
"""移動平均によるスムージング"""
return np.convolve(data, np.ones(window_size) / window_size, mode='same')
def plot_fft_difference(self):
fig, axs = plt.subplots(2, 1, figsize=(15, 10)) # スムージング前後の2つのグラフエリア
self._plot_fft_difference(axs[0], smooth=False) # スムージング前
self._plot_fft_difference(axs[1], smooth=True) # スムージング後
axs[0].set_title("FFT Difference (Original)")
axs[1].set_title("FFT Difference (Smoothed)")
plt.tight_layout()
plt.show()
def _plot_fft_difference(self, ax, smooth):
min_freq = 20 # 最小周波数
max_freq = 20000 # 最大周波数
ax.set_xlabel('Frequency (Hz)')
ax.set_ylabel('Difference (dB)')
ax.set_xscale('log')
ax.set_xticks([min_freq, 50, 100, 500, 1000, 5000, 10000, max_freq])
ax.set_xlim(min_freq, max_freq)
ax.set_ylim(-20, 20)
ax.grid(True, which='major', linestyle='-')
ax.grid(True, which='minor', linestyle=':')
formatter = EngFormatter(unit='', sep='')
ax.xaxis.set_major_formatter(formatter)
# 最初のデータを基準に他のデータとの差を計算
base_data = self.original_data[0]
base_rate = self.rates[0]
N = len(base_data)
base_fft = np.fft.fft(base_data * np.hanning(N))
base_freqs = np.fft.fftfreq(N, 1 / base_rate)[:N // 2]
base_magnitude = np.abs(base_fft)[:N // 2]
base_magnitude_db = 20 * np.log10(base_magnitude / np.max(base_magnitude))
for i, data in enumerate(self.original_data[1:]): # 2つ目以降のデータと比較
N = len(data)
fft_result = np.fft.fft(data * np.hanning(N))
freqs = np.fft.fftfreq(N, 1 / self.rates[i + 1])[:N // 2]
fft_magnitude = np.abs(fft_result)[:N // 2]
fft_magnitude_db = 20 * np.log10(fft_magnitude / np.max(fft_magnitude))
# 差分の計算
valid_indices = np.logical_and(base_freqs >= min_freq, base_freqs <= max_freq)
freq_diff = base_freqs[valid_indices]
magnitude_diff = base_magnitude_db[valid_indices] - fft_magnitude_db[valid_indices]
# スムージング
if smooth:
magnitude_diff = self.smooth(magnitude_diff, window_size=20)
# 差分のプロット
ax.plot(freq_diff, magnitude_diff, label=f'{self.file_names[0]} - {self.file_names[i + 1]}')
ax.legend(bbox_to_anchor=(0.5, -0.1), loc='upper center', fontsize='medium', ncol=2)
# データを保持するリスト
original_data = []
rates = []
file_name_x = []
# 対象のフォルダ
folder_path = '/Users/~フォルダのパス'
# フォルダ内のすべてのWAVファイルを処理
for file_name in os.listdir(folder_path):
if file_name.endswith('.wav'):
file_path = os.path.join(folder_path, file_name)
rate, data = wavfile.read(file_path)
if data.ndim > 1: # ステレオの場合、片方のチャンネルを取得
data = data[:, 0]
data = data / np.max(np.abs(data)) # データの規格化
original_data.append(data)
rates.append(rate)
file_name_x.append(file_name)
# 描画
plotter = FFTDifferencePlotter(original_data, rates, file_name_x)
plotter.plot_fft_difference()