
【マクロ経済学note】IS-LMモデル演習
『マクロ経済学note』シリーズでは、経済学の初学者、特に文系出身の(あるいは数学が苦手な)学生を対象として、マクロ経済学の解説を行う。このnoteは『IS-LMモデル演習』と題し、学部マクロの最初の山場、IS-LMモデルの計算問題を中心とした問題演習および解説を行う。IS-LMモデルは多くの大学の入門~中級レベルのマクロ経済学で学習することになる代表的なマクロ経済モデルであるとともに、資格試験・公務員試験から大学院入試まで、経済学を課する幅広い試験で極めて高い頻度で出題される最重要論点でもある。そのため、単に理論を理解するだけでなく、実際の手計算を必要とするような練習問題をたくさん解きたいという需要も大きいだろう。このnoteはそのような需要に応えるために作成している。
なお、このnoteではIS-LM分析に向けての前提となる各知識について一から解説はしない。『マクロ経済学note』シリーズは本noteを足がかりに順次拡大していく予定であるが、この文章が読者に表示されている現時点においてはまだ鋭意執筆中の段階である。そのため、もし完全な理解を望むのであれば、公刊されているテキストを頼る必要がある。読者が経済学部生で、大学で指定のテキストがあるのであれば、それを利用するのも良いだろう。もし、これから何らかのマクロ経済学の教科書を購入する必要があるという方がいるならば、特におすすめできる本として齊藤他『マクロ経済学』を挙げる。本書は初学者にはやや難しいものの、この一冊があればIS-LMモデルのみならず学部レベルのマクロ経済学で必要な知識は網羅されているため、コスパに優れている。また、索引が非常に丁寧なため、各内容を辞書的に調べる際にも重宝できる。ただしDSGEなど大学院のコア・マクロで学ぶ内容までは、当然だが十分にカバーされていないため、大学院進学希望者は本書を足がかりにして、次のステップに進むと良いだろう。
1. IS-LM分析の基本知識
1.1 IS-LM分析とは
IS-LMモデルは、ケインズの『雇用・利子および貨幣の一般理論』(いわゆる一般理論)のトイ・モデルの一つで、新古典派の経済学者ヒックスによって開発された(Hicks(1937))ものである。ヒックスのモデルを拡張した経済学者ハンセンの名と合わせて、ヒックス=ハンセンモデルとも呼ばれている。一般理論はそれまでの古典派経済学の考え方(=自由放任主義)を打ち崩すセンセーショナルな大論文であったが、随所に様々な新しいアイデアが散りばめられた複雑難解なものであったため、それが今までの古典派経済学とどう違っているのかという「解説」が求められていた。IS-LMモデルはその「解説」の一つであり、一般理論のトイ・モデルは他にも45度線モデル、AD-ASモデル、それらの派生モデルなど、多数存在している。

右:Hicks (1937)より引用 オリジナルのモデルでは所得水準をIとしている
1.2 IS-LM分析で用いられている理論の整理
IS-LMモデルは、一般理論から生産物市場の理論と資産市場(=貨幣・債券市場)の理論を抽出し、両市場の相互作用を分析するモデルである。まずは各市場の理論として、どのようなアイデアが用いられているかを整理しよう。
生産物市場の理論(概要)
A. 有効需要の原理
生産物の供給は、その有効需要の大きさによって決定される。また、有効需要の内訳は、閉鎖経済においては家計の消費支出、企業の投資支出、政府の政府支出に分けられる。
B. GDP三面等価の原則
生産物の総産出量と国民所得は事後的に一致する。
C. 絶対所得仮説(ケインズの消費理論)
消費支出の水準は現在の国民所得水準に依存する。
※A〜Cの理論で45度線モデルの主張の一つである『乗数効果』が導かれる。
D. 乗数効果
有効需要が増加すると、消費の波及的増加を経て、国民所得はその何倍も増加する。
E. 資本の限界効率理論(ケインズの投資理論)
投資支出の水準は利子率に依存する。利子率が低下すると採算のとれるプロジェクトが増えるため、投資支出が増える。
※A〜Eの理論を統合した結果として、IS曲線が導出される。
F. IS曲線
政府支出が一定のもとで利子率が低下すると、生産物市場が均衡する国民所得水準が増加する。よって生産物市場が均衡するときの利子率と国民所得の関係として右下がりのグラフが描かれる。
(IS曲線のメカニズム)
利子率低下⇨投資支出増加⇨有効需要増加⇨総産出量増加⇨国民所得増加
*政府支出が増加する(財政出動)と、IS曲線が右方シフトする。

IS曲線の左下側では生産物市場は超過需要(超過投資)
IS曲線の右上側では生産物市場は超過供給(超過貯蓄)
資産市場の理論(概要)
G. 資産価格決定理論(効率的市場仮説)
利子率が低下すると国債など資産価格は上昇する。
H. 流動性選好説
公衆が貨幣を需要する動機には、取引動機・予備的動機に基づく取引需要と投機的動機に基づく資産需要がある。取引需要は所得水準と正の相関がある一方、資産需要は資産価格と正の相関がある(投機家は債券や株式の価格が安値のときに拾い買い、高値のときに売り抜けようとするため)。また、貨幣供給が増加したときには、原則として資産需要が増加する形で貨幣市場の需給が保たれる。
※G,Hの理論を統合した結果として、LM曲線が導出される。
I. LM曲線
実質貨幣供給量が一定のもとで利子率が低下すると、貨幣市場が均衡する国民所得水準が減少する。よって貨幣市場が均衡するときの利子率と国民所得の関係として右上がりのグラフが描かれる。
(LM曲線のメカニズム)
利子率低下⇨債券価格上昇⇨債券需要減少⇨資産需要増加⇨取引需要減少⇨国民所得減少(生産物市場に対する国民所得減少の圧力となる)
*物価水準が一定のもとでマネー・サプライ(名目貨幣供給量)が増加する(金融緩和)と、LM曲線が右方シフトする。
※中央銀行がマネー・サプライをコントロール可能であることを明示するために次の理論も用いられる。
J. 信用創造
ハイパワード・マネーが増加すると、マネー・サプライはその何倍も増加する。
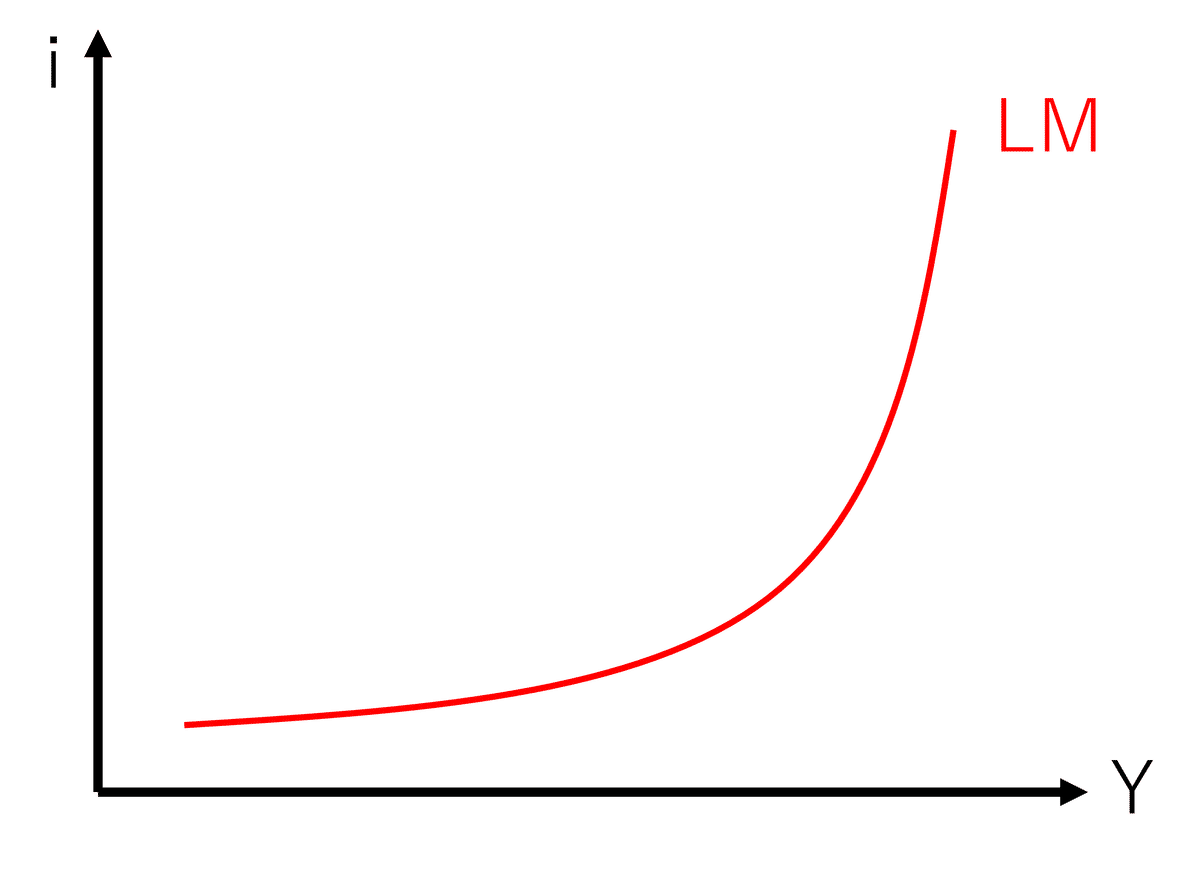
LM曲線の右下側では貨幣市場は超過需要(債券市場超過供給)
LM曲線の左上側では貨幣市場は超過供給(債券市場超過需要)
特に利子率が低い水準ではLM曲線は水平に近づく(流動性の罠)
これらの理論を統合して得られる、右下がりのIS曲線と右上がりのLM曲線の交点が生産物市場と金融市場の同時均衡と呼ばれる状態で、他の要素が一定のもとで生産物市場と金融市場がともに均衡するためには、特定の利子率水準(均衡利子率)と特定の国民所得水準(均衡国民所得)が成立しなければならないことを主張している。IS-LM分析とはすなわち、この同時均衡が政府支出やマネー・サプライをはじめとした各種外生変数の変化によってどのように遷移するかを分析するものである。
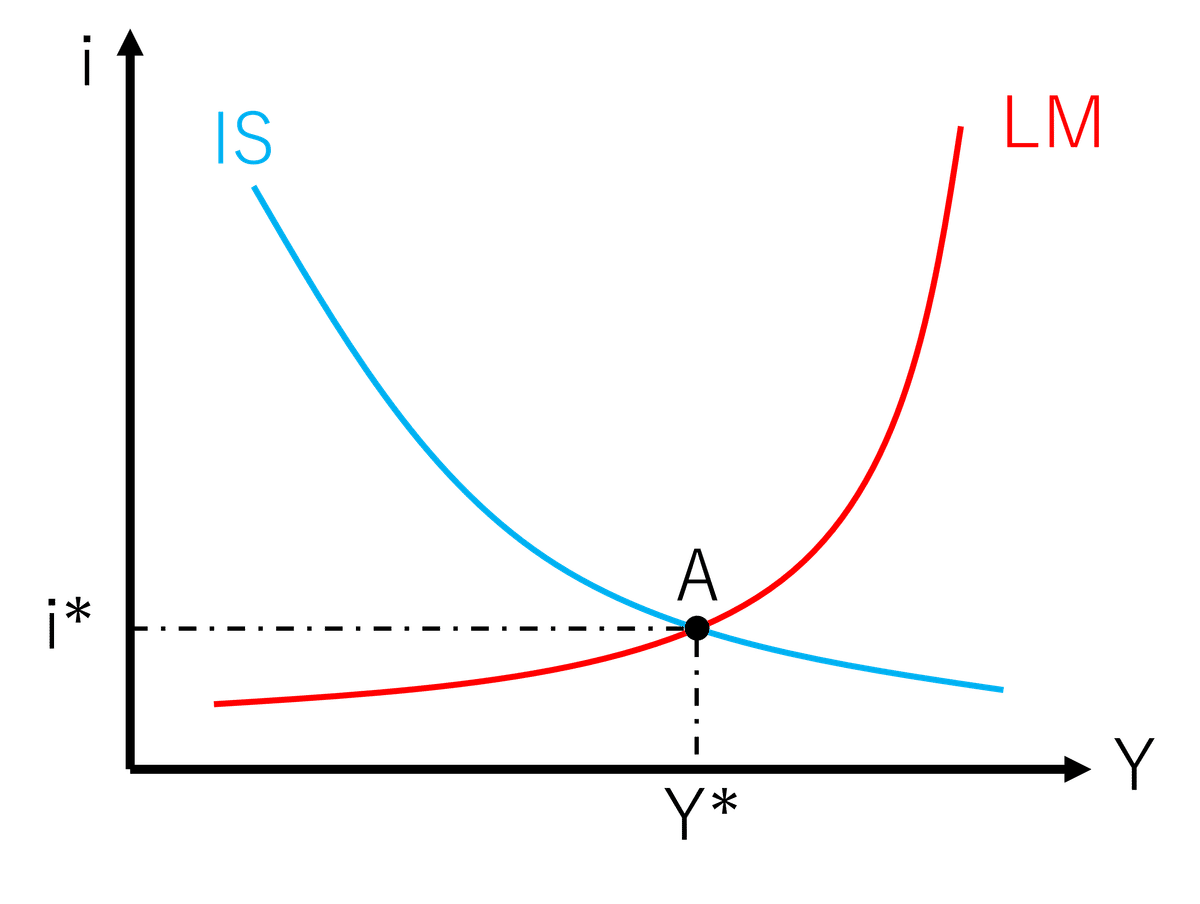
同時均衡における縦軸の値が均衡利子率
同時均衡における横軸の値が均衡国民所得
1.3 「標準モデル」
次に、IS-LMモデルで用いられる数式と記号について説明する。このnoteでは極力、現行の教科書の主流の記法に倣うことに努めるが、皆さんが直面することになる個別の問題では異なる記号が充てられている可能性もあるし、また問題では式に説明はついていないことが多いため、実戦の際には一問一問、式と記号の意味を指差し確認して欲しい。このnoteでは、以下の式のラインナップで表されるマクロ経済モデルを閉鎖経済の標準モデルと呼ぶことにする。
IS-LMモデル(閉鎖経済の標準モデル)
①$${Y=C+I+G}$$ 生産物市場の均衡条件
②$${C=C_{0}+c(Y-T)}$$ ケインズ型消費関数
③$${T=T_{0}+tY}$$ ケインズ型租税関数
④$${I=I_{0}-bi}$$ ケインズ型投資関数
⑤$${G=G_{0}}$$
⑥$${\frac{M_{S}}{P}=L_{1}(Y)+L_{2}(i)}$$ 金融市場の均衡条件
⑦$${M_{S}=M_{S0}}$$
⑧$${P=P_{0}}$$
⑨$${L_{1}(Y)+L_{2}(i)=\alpha +\beta Y-\gamma i}$$ 貨幣需要関数
記号一覧
$${Y}$$:国民所得 $${C}$$:消費支出 $${I}$$:投資支出 $${G}$$:政府支出
$${C_{0}}$$:基礎消費 $${c}$$:限界消費性向 $${Y-T}$$:可処分所得 $${T}$$:租税
$${T_{0}}$$:最低課税 $${t}$$:限界税率
$${I_{0}}$$:最大投資 $${b}$$:投資の利子弾力性(代理変数) $${i}$$:利子率
$${\frac{M_{S}}{P}}$$:実質貨幣供給量
$${M_{S}}$$:マネー・サプライ $${P}$$:物価水準
$${L_{1}(Y)}$$:取引需要 $${L_{2}(i)}$$:資産需要
$${\alpha}$$, $${\beta}$$, $${\gamma}$$:パラメータ
$${C_{0}}$$,$${T_{0}}$$,$${I_{0}}$$,$${G_{0}}$$,$${M_{S0}}$$,$${P_{0}}$$:外生変数
①〜④式が生産物市場に関する式で、これらの連立方程式を解いて$${i}$$と$${Y}$$の関係に表したものがIS曲線である。また、⑤,⑥式は金融市場に関する式で、これらの連立方程式を解いて$${i}$$と$${Y}$$の関係に表したものがLM曲線である。さらにIS曲線とLM曲線を連立方程式として解くと、その交点である同時均衡が求められる。
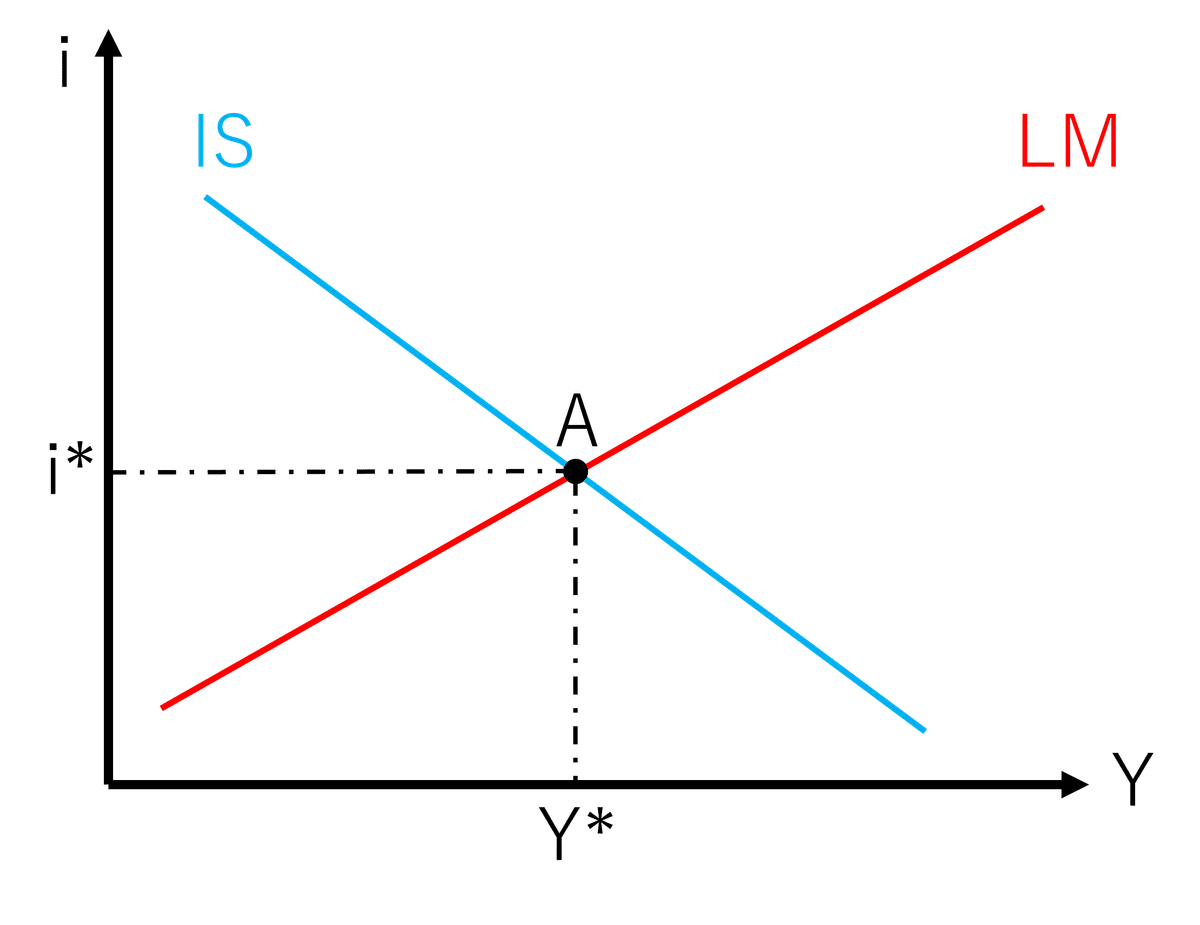
実際に同時均衡を求めてみよう。①~④式の連立方程式を解くとIS曲線が
⑦$${Y=\frac{1}{1-c+ct}(C_{0}+I_{0}+G-cT_{0}-bi)}$$
と導出される。また⑤,⑥式よりLM曲線が
$${i=\frac{\alpha}{\gamma}-\frac{1}{\gamma P}M_{S}+\frac{\beta}{\gamma}Y}$$
と導出される。ここで記号を単純化するために
$${\frac{\alpha}{\gamma}=A}$$,$${\frac{1}{\gamma P}=j}$$,$${\frac{\beta}{\gamma}=k}$$とするとLM曲線は
⑧$${i=A-jM_{S}+kY}$$
と置き換えられる。ここで⑦式と⑧式の連立方程式を解けば
⑨$${Y^{*}=\frac{1}{1-c+ct+bk}(C_{0}+I_{0}+G-cT_{0}+bjM_{s}-bA)}$$
が得られる。これが均衡国民所得である(さらにこれを⑧式に代入することで均衡利子率が得られるが、ここでは省略する)。
さて、先ほど書いた通り、IS-LM分析は同時均衡が外生変数の変化によってどう遷移するかを調べることが主目的である。この外生変数をXとすると、外生変数Xの変化に対する国民所得水準$${Y}$$の変化の比率のことをX乗数と呼ぶ。X乗数を求めたければ、⑨式に対して外生変数Xと$${Y^{*}}$$について差分を取る。たとえば政府支出乗数を求めたければ、⑨式に対して$${G}$$と$${Y^{*}}$$について差分を取り
$${\Delta Y^{*}=\frac{1}{1-c+ct+bk}\Delta G}$$
となることから、政府支出乗数は$${\frac{1}{1-c+ct+bk}}$$と求められる。
以上の工程をさまざまな外生変数に対して行うことで、以下の乗数のラインナップが得られる。ただし、定額税均衡予算乗数は政府支出の財源として同額の定額税の増税($${\Delta G=\Delta T_{0}}$$)をすることを、均衡予算乗数は政府支出の財源として同額の租税全体の増税($${\Delta G=\Delta T}$$)をすることを、中央銀行引き受け乗数は政府支出の財源として中央銀行引き受け方式の国債発行($${\Delta G=\Delta H}$$)を行うことをそれぞれ意味する。
乗数一覧(閉鎖経済の標準モデル)
独立投資乗数 $${\Delta Y=\frac{1}{1-c+bk+ct}\Delta I_{0}}$$
政府支出乗数 $${\Delta Y=\frac{1}{1-c+bk+ct}\Delta G}$$
定額税乗数 $${\Delta Y=\frac{-c}{1-c+bk+ct}\Delta T_{0}}$$
定額税均衡予算乗数 $${\Delta Y=\frac{1-c}{1-c+bk+ct}\Delta G(=\Delta T_{0})}$$
均衡予算乗数 $${\Delta Y=\frac{1-c}{1-c+ct}\Delta G(=\Delta T)}$$
マネー・サプライ乗数 $${\Delta Y=\frac{bj}{1-c+bk+ct}\Delta M_{S}}$$
中央銀行引き受け乗数 $${\Delta Y=\frac{1+bjμ}{1-c+bk+ct}\Delta G(=\Delta H)}$$
※$${μ}$$は貨幣乗数(信用乗数),$${H}$$はハイパワード・マネー
さらに、標準モデルに開放経済の要素が加わったモデルでケインズ型輸入関数$${IM=IM_{0}+mY}$$が導入されると、標準モデルは次のようなラインナップになる。このモデルは開放経済の標準モデルと呼ぶことにしよう。
IS-LMモデル(開放経済の標準モデル)
①$${Y=C+I+G+EX-IM}$$ 生産物市場の均衡条件
②$${C=C_{0}+c(Y-T)}$$ ケインズ型消費関数
③$${T=T_{0}+tY}$$ ケインズ型租税関数
④$${I=I_{0}-bi}$$ ケインズ型投資関数
⑤$${G=G_{0}}$$
⑥$${EX=EX_{0}}$$
⑦$${IM=IM_{0}+mY}$$ ケインズ型輸入関数
⑤$${\frac{M}{P}=L_{1}(Y)+L_{2}(i)}$$ 金融市場の均衡条件
⑥$${L_{1}(Y)+L_{2}(i)=\alpha +\beta Y-\gamma i}$$ 貨幣需要関数
記号一覧
$${Y}$$:国民所得 $${C}$$:消費支出 $${I}$$:投資支出 $${G}$$:政府支出 $${EX}$$:輸出 $${IM}$$:輸入
$${C_{0}}$$:基礎消費 $${c}$$:限界消費性向 $${Y-T}$$:可処分所得
$${T}$$:租税$${T_{0}}$$:最低課税 $${t}$$:限界税率
$${I_{0}}$$:最大投資 $${b}$$:投資の利子弾力性(代理変数) $${i}$$:利子率
$${EX_{0}}$$:独立輸出 $${IM_{0}}$$:独立輸入 $${m}$$:限界輸入性向
$${\frac{M_{s}}{P}}$$:実質貨幣供給量 $${M_{s}}$$:マネー・サプライ $${P}$$:物価水準$${L_{1}(Y)}$$:取引需要 $${L_{2}(i)}$$:資産需要$${\alpha}$$, $${\beta}$$, $${\gamma}$$:パラメータ
$${C_{0}}$$,$${T_{0}}$$,$${I_{0}}$$,$${G_{0}}$$,$${EX_{0}}$$,$${IM_{0}}$$,$${M_{S0}}$$,$${P_{0}}$$:外生変数
輸入関数の存在により、開放経済においては乗数効果が弱まり、限界輸入性向$${m}$$を用いて乗数は次のように改められる。ただし、これはマンデル=フレミングモデルのような外国為替市場や国際資本移動の存在は想定していないモデルでのみ用いることができる。
乗数一覧(開放経済の標準モデル)
独立投資乗数 $${\Delta Y=\frac{1}{1-c+bk+ct+m}\Delta I_{0}}$$
政府支出乗数 $${\Delta Y=\frac{1}{1-c+bk+ct+m}\Delta G}$$
独立輸出乗数 $${\Delta Y=\frac{1}{1-c+bk+ct+m}\Delta X}$$
独立輸入乗数 $${\Delta Y=\frac{-1}{1-c+bk+ct+m}\Delta M_{0}}$$
定額税乗数 $${\Delta Y=\frac{-c}{1-c+bk+ct+m}\Delta T_{0}}$$
定額税均衡予算乗数 $${\Delta Y=\frac{1-c}{1-c+bk+ct+m}\Delta G(=\Delta T_{0})}$$
均衡予算乗数 $${\Delta Y=\frac{1-c}{1-c+ct+m}\Delta G(=\Delta T)}$$
マネー・サプライ乗数 $${\Delta Y=\frac{bj}{1-c+bk+ct+m}\Delta M_{S}}$$
中央銀行引き受け乗数 $${\Delta Y=\frac{1+bjμ}{1-c+bk+ct+m}\Delta G(=\Delta H)}$$
標準モデルから外れる他の応用も色々あり得るが、簡単な応用としては限界投資性向が導入される
$${I=eY-bi}$$
パターンや、消費関数の代わりに貯蓄関数を与える
$${S=s(Y-T)-S_{0}}$$
パターンが考えられる。前者の場合には、乗数の分母に$${-e}$$を加えれば良く、後者の場合は限界消費性向と限界貯蓄性向の和が1($${c+s=1}$$)であることを利用して$${c}$$を求めれば良い(もしくは乗数の分母$${1-c}$$が限界貯蓄性向なので、そのまま代入しても良い)。
1.4 「3つのスイッチ」
実は最後の開放経済モデルの乗数を覚えておくだけで、45度線分析とIS-LM分析のほぼあらゆるタイプの乗数の問題に対応できる。その際、意識しなければいけないのは、「3つのスイッチ」をモデルごとにON/OFFするということだ。
「3つのスイッチ」
1⃣『IS-LM』スイッチ:IS-LMモデルでは乗数の分母に$${bk}$$がON
2⃣『所得税』スイッチ:租税関数モデルでは乗数の分母に$${ct}$$がON
3⃣『開放経済』スイッチ:開放経済モデルでは乗数の分母に$${m}$$がON
たとえば今から解く問題が、45度線分析、所得税あり、開放経済モデルの財政出動に関する問題であればスイッチ1⃣のみOFFにして政府支出乗数$${=\frac{1}{1-c+ct+m}}$$を用いれば良いし、IS-LM分析、所得税なし、閉鎖経済モデルの増税に関する問題であればスイッチ2⃣と3⃣をOFFにして定額税乗数$${=\frac{-c}{1-c+bk}}$$を用いれば良い。
また、3つのスイッチのそれぞれがONになると、各乗数は小さくなる。その中でもスイッチ1⃣$${bk}$$の効果は利子率の上昇に伴う投資の減少、いわゆるクラウディング・アウト効果によるもので、スイッチ2⃣$${ct}$$の効果は所得税の持つビルトイン・スタビライザー効果によるものである。
1.5 IS曲線、LM曲線の「シフト幅」
最後の準備として、財政政策や金融政策によってIS曲線やLM曲線がシフトする際の「シフト幅」について考えよう。先程導出した式からもう一度抜き出すと、標準モデルではIS曲線とLM曲線はそれぞれ
⑦$${Y=\frac{1}{1-c+ct}(C_{0}+I_{0}+G-cT_{0}-bi)}$$
⑧$${i=A-jM_{S}+kY}$$
と求められた。ここから財政出動によるIS曲線の右シフト幅を求めたければ、⑦式から$${Y}$$と$${G}$$について差分を取る(つまり$${\Delta i=0}$$することで$${Y}$$軸方向への移動のみを見ている)。すると
$${\Delta Y=\frac{1}{1-c+ct}\Delta G}$$
が得られる。同様に、金融緩和によるLM曲線の右シフト幅を求めたければ、⑧式から$${Y}$$と$${M_{S}}$$について差分を取る。すると
$${\Delta Y=\frac{j}{k}\Delta M_{S}}$$
が得られる。
IS曲線とLM曲線の「シフト幅」(閉鎖経済モデル)
財政出動によるIS曲線のシフト幅 $${\Delta Y=\frac{1}{1-c+ct}\Delta G}$$
金融緩和によるLM曲線のシフト幅 $${\Delta Y=\frac{j}{k}\Delta M_{S}}$$
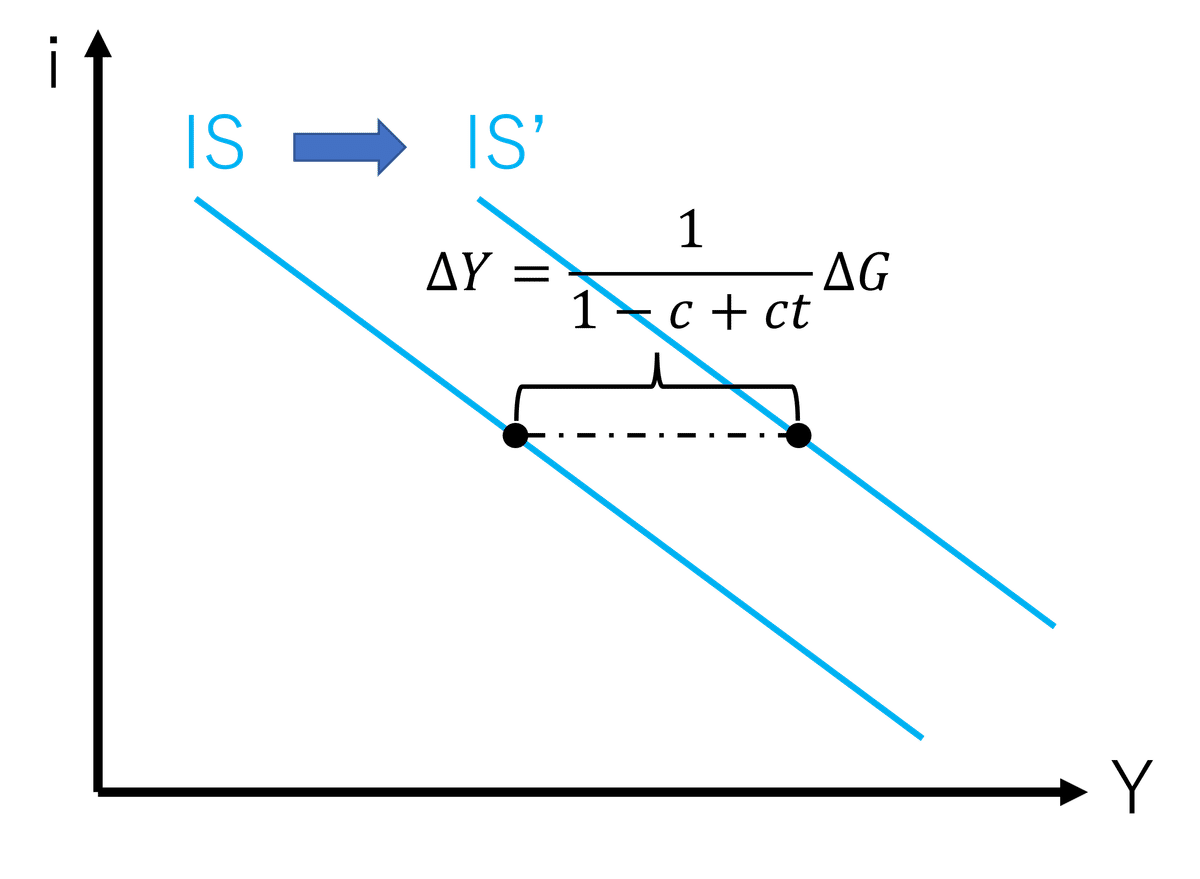

この「シフト幅」はIS-LMモデルの計算問題(特にクラウディング・アウト関連)を解く際にしばしばお世話になるので、できれば覚えておきたい。なお、IS曲線の右シフト幅に現れる$${\frac{1}{1-c+ct}}$$は45度線モデルにおける政府支出乗数と一致する(したがって、開放経済モデルにおいては$${\frac{1}{1-c+ct+m}}$$となる)。また、LM曲線の右シフト幅は$${j=\frac{1}{γP}\Delta M_{S}}$$であるが、この式を変形すると$${\Delta M_{S}=γkP\Delta Y}$$となる。この形は古典派貨幣理論を代表するケンブリッジ方程式(マーシャルの現金残高方程式)に対応する式になっている($${γk}$$がいわゆるマーシャルのk)。
以上の基本知識をもって、さまざまなIS-LMモデルの問題に取り組んでみよう。ここからは有料記事になるので、購入するかどうかはここまでの記事を読んで熟考してから決めてほしい。なお、用意されている問題のパターンは全部で10パターン、問題数は全30問ある。おそらく、市販の教科書や問題集でここまでIS-LMモデルばかりねちっこく扱っているものはないだろう。この演習をやり込めば、IS-LMモデルがあなたの得点源になることは間違いない。
ここから先は
¥ 300
この記事が気に入ったらチップで応援してみませんか?
