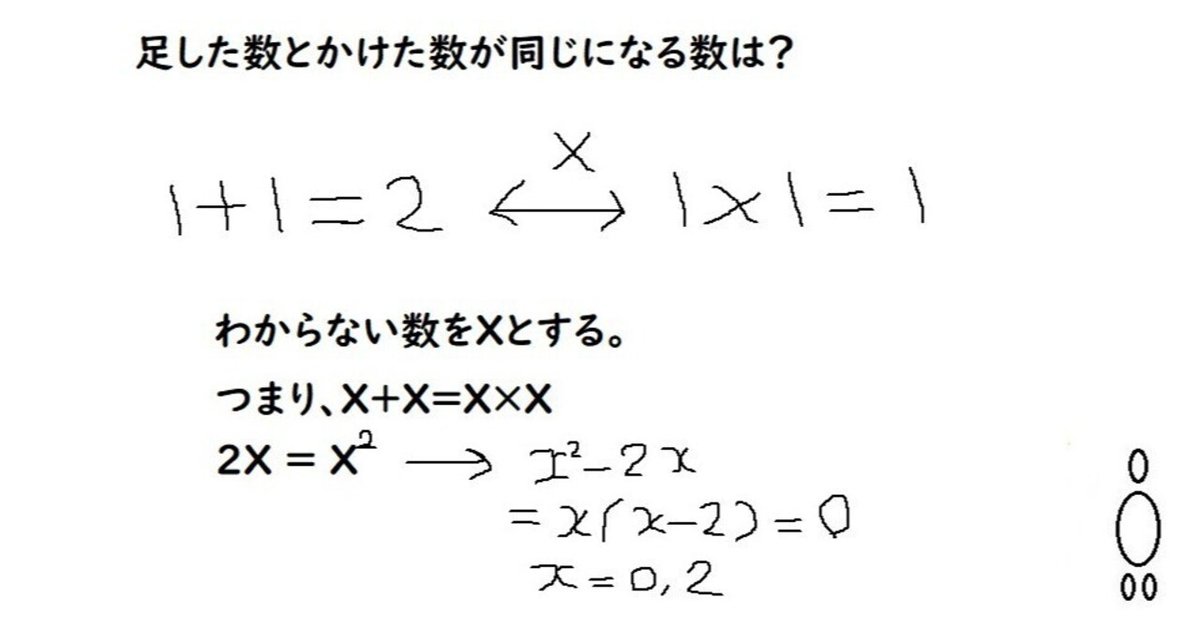
６歳の子供に説明できなければ理解したとは言えない＃２６「さんすうっておもしろい」

生きていて身の回りに出てくるのは、ほとんど数学ではなく、さんすうだ。なので、まず、さんすうを楽しみ、数字を楽しむ習慣をつけると生きるのも楽しくなるかも。
頭の中で、足しても、かけても同じ数になる数ってあるのかな？と疑問を持ったとしよう。答えなんかどうでもいい。疑問を持った、じゃあ、次なにする。数字遊びで考えてみよう。例えば、１。１足す１は２。１かける１は１。なので、足した場合とかけた場合で違う数になる。じゃあ、１０は？１０たす１０＝２０，１０かける１０＝１００。うわーどんどんチガくなってく。じゃあ、５。５たす５は１０。５かける５は２５だ。そんな数ないんじゃないの？

疑問を持った、ちょっと考えた、あきらめた。
おーい、あきらめが早すぎ。なんかよくわからない数（まあ、答え）を仮にAとしよう。このAはこんな感じでつかう。なにかわからない数を２倍すると６になった。じゃあ、わからない数はいくつ？わからない数Ａ × 2 (
つまり２倍）＝６　なので、Aは３だ！こういうふうにつかう。さっきのやつは、足した数とかけた数が同じ、ということなので、足した数 A + A = 2 A が、かけた数 A×A と同じ⇒ 2A = A×A ということだ。どちら側にもＡがついているので、Ａが「ふつう」の数だとおかしなことになる。だって、左側は２倍しているのに、右側はＡ倍している。これが同じになるはずがない。つまりふつうの数でない「０」ならばどうだろう。０を２倍すると０、０かける０は０、なので、同じになるではないか！
じゃあ、答えはそれだけか？よーくみると、左側に２がついている。なので、Ａが２のとき、２×２＝２×２となり、同じになる！
がっこーだと、X(X-2) = 0　のように「因数分解」できて、X = 0, 2 が答え。と教わるだろうが、そんなの知らないよ。よーくみるとわかる、そこから始めてみては。「考える」とはそういうこと。答えがでればいい、わけではない。