
ヤンキーでもわかる尤度と確率の違い
確率は事象の可能性
例えば君が大量にピカチュウをゲットした時
それらの体重を慎重にはかり、平均体重が32kgで標準偏差が2.5
の正規分布だと仮定する

これの分布を図に書くとこんな感じになると仮定する

ここでランダムにピカチュウを1匹とってきて
その体重が32kgから34kgだった時の確率は…
下図のように、曲線とx軸が囲む面積になる!
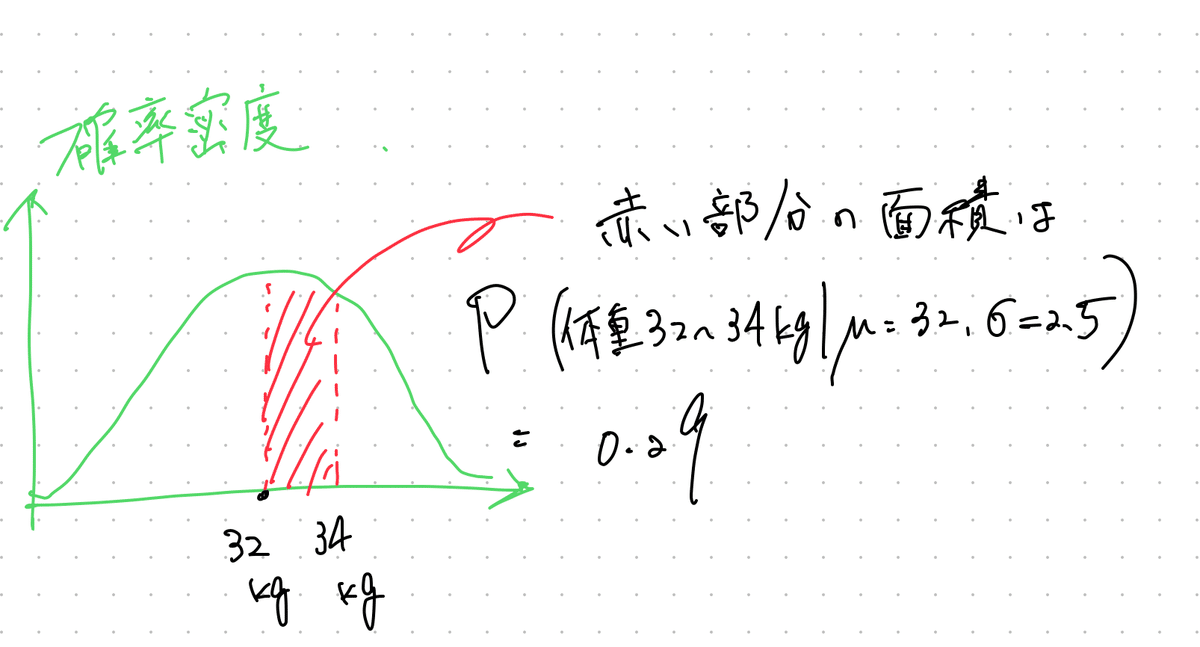
もし34kg以上確率を知りたい時はこの曲線を動かさないで
先ほどよりも右側の部分の面積が求める値になる
尤度は分布の可能性
尤度を考える場合は面積ではなく、点で考える
例えば、ピカチュウの体重が34kgだと仮定するとき
平均32kg、標準偏差が2.5の分布のy軸の値は0.12になる

これは面積ではなく点なので、確率ではない別の言葉「尤度」と呼ばれる
確率と尤度は論理が逆なだけ
さっき見てきたように確率は面積、尤度は点で見ていることが大きな違いだった
もう少し踏み込んで理解してみると違いがわかるようになる
確率の計算では
平均体重が32kgで標準偏差が2.5だと仮定することを先にして
尤度の計算では
ピカチュウの体重が34kgだと仮定した
仮定しているものがそれぞれ
確率;確率分布
尤度;事象
いうふうに違うのだ
つまり確率は
前提としてピカチュウの平均体重が32kgで標準偏差が2.5(確率分布)の時
34kgのピカチュウが出る(事象)可能性は
0.375(=確率)
尤度は
前提として34kgのピカチュウが出る(事象)の時
最終的にピカチュウの平均体重が32kgで標準偏差が2.5(確率分布)である可能性は
0.12(=尤度)
というふうに
前提と最後の結論の論理が逆になっているだけなのである
