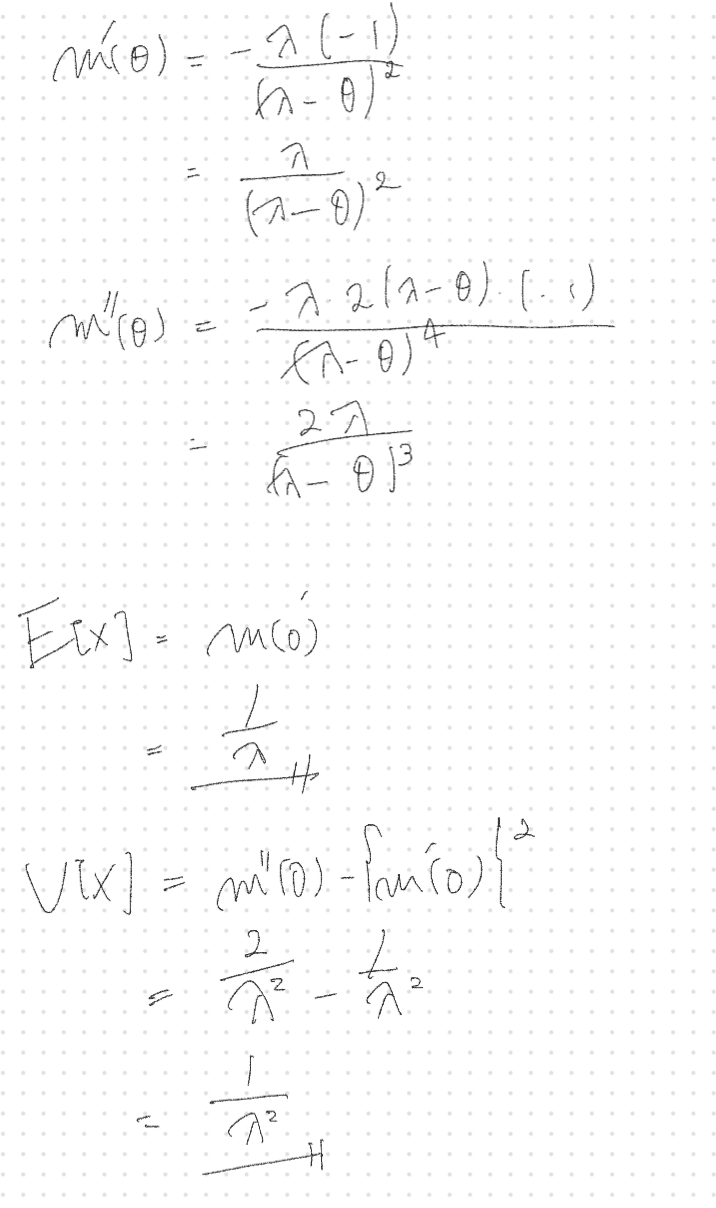統計準1級 第2章 確率分布と母関数 解説
確率分布の諸関数
確率(分布)関数
確率変数$${X}$$が値$${x}$$をとるときの確率$${p(x) = P(X = x)}$$を確率関数といい、離散型の場合は確率質量関数、連続型の場合は確率密度関数と呼ばれる
累積分布関数
確率密度関数を与えられた区間内で積分したもの
離散型確率密度関数だとシグマ
連続型確率密度関数だとインテグラルで積分する
同時確率関数・周辺確率関数・条件付き確率関数
同時確率関数 :
$${X = x}$$をとると同時に$${Y = y}$$をとるときの確率関数
周辺確率関数 :
同時確率関数の$${X = x}$$か$${Y = y}$$どちらか積分してやるだけ
条件付き確率関数 :
同時確率関数と周辺確率関数から求められる(下記式参照)
$$
f (y | x) (条件付き確率関数) \\{}\\ \\{}\\
= \frac{f(x,y) (x,yの同時確率関数)}{f_{X}(x) (xの周辺確率関数)}
$$
実施に計算してみればわかる
例題 :

母関数
確率変数の平均、分散などの統計量を計算するときに母関数という概念を用いる
確率変数が整数値をとる離散型のときは確率母関数を使い
確率変数が非整数値をとる連続型のときはモーメント母関数を使う
確率母関数
$${s}$$を任意の実数として
これと確率変数の指数関数の期待値が確率母関数となる
$$
G(s) = E[s^X] = \sum_{x} s^x p(x)
$$
この$${G(s)}$$の1階微分と2回微分を計算し
それぞれの$${s}$$に1を代入したものが平均と分散の計算に使える
$$
E[X] = G'(1)
$$
$$
V[X] = G''(1) + G'(1) - (G'(1))^2
$$


モーメント母関数
先ほどの確率母関数において$${s = e^\theta}$$と置換してやるだけ
$$
m(\theta) = E[e^{\theta X}] = G(e^{\theta})
$$
平均と分散は下記のように計算する
$$
E[X] = m'(0)
$$
$$
V[X] = m''(0) - (m'(0))^2
$$