
ヤンキーでもわかる中心極限定理
めっちゃデータとってきたら平均が正規分布
統計学で
中心極限定理が「素晴らしい定理」とよく言われるが
ヤンキーにとっては
「ちょっと何言ってるか分からない」

となるだろう(私もそう思っている)
ひとことで言うと
母集団がどんな分布(ポアソン分布だとか2峰性の分布)
に従ってても
そこからとってきた
大量のサンプルサイズの標本平均は
正規分布に従う
ピカチュウで例えると
ピカチュウの体重がどんな分布(例えば2峰性の分布)
に従ってても

大量のピカチュウ(10000匹くらい)の標本内の平均体重は正規分布に従う

実際のサンプルサイズ増やしていった時のイメージ
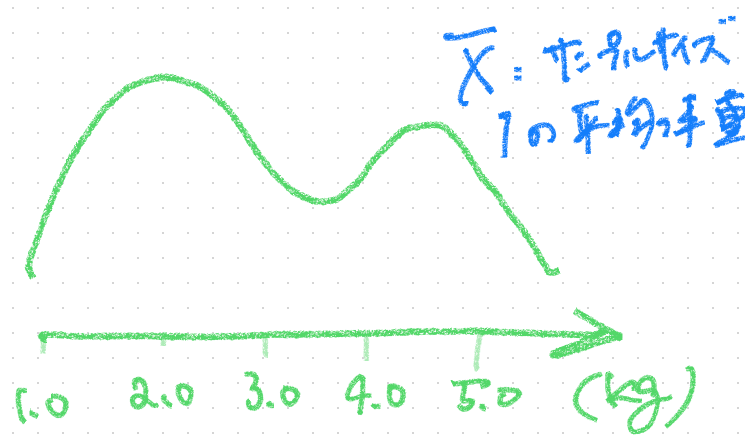
例としてサンプルサイズ1の時を考えてみよう
これは元データそのものと同じなので
標本平均の分布を書いても何も変わらない
次にサンプルサイズ2の時は
とくに右側と左側の点から平均をとった場合は平均が真ん中に来る

なので標本平均の分布は少し真ん中による
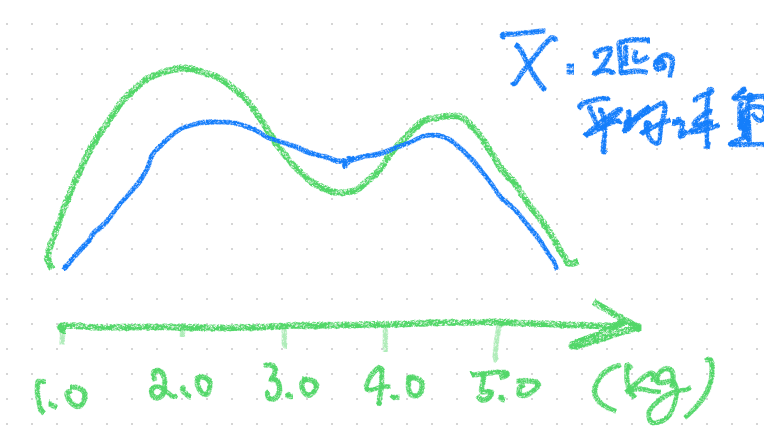
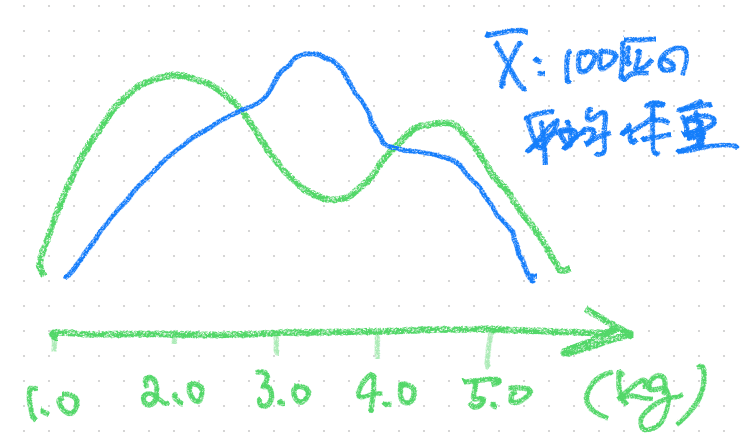
次にサンプルサイズ100の時は
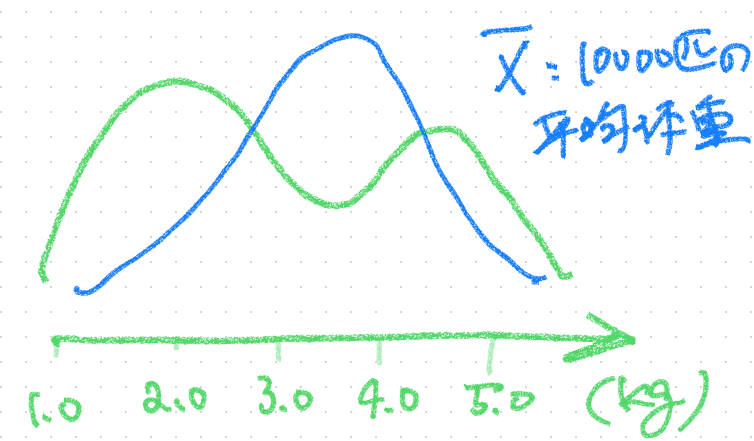
次にサンプルサイズ10000の時は
結局なんで正規分布になるの?
サンプルサイズを増やしたら
極端に小さな値を取る点が
極端に大きな値を取る点によって打ち消される
(サンプルサイズ2の時みたいに)
回数が多くなる
↓
標本平均の真ん中に点が集まって
山ができる
というイメージがあれば
中心極限定理のイメージは簡単になる
