統計準1級　第10章　検定の基礎と検定法の導出　解説

2024年4月12日 00:49

検定の過誤

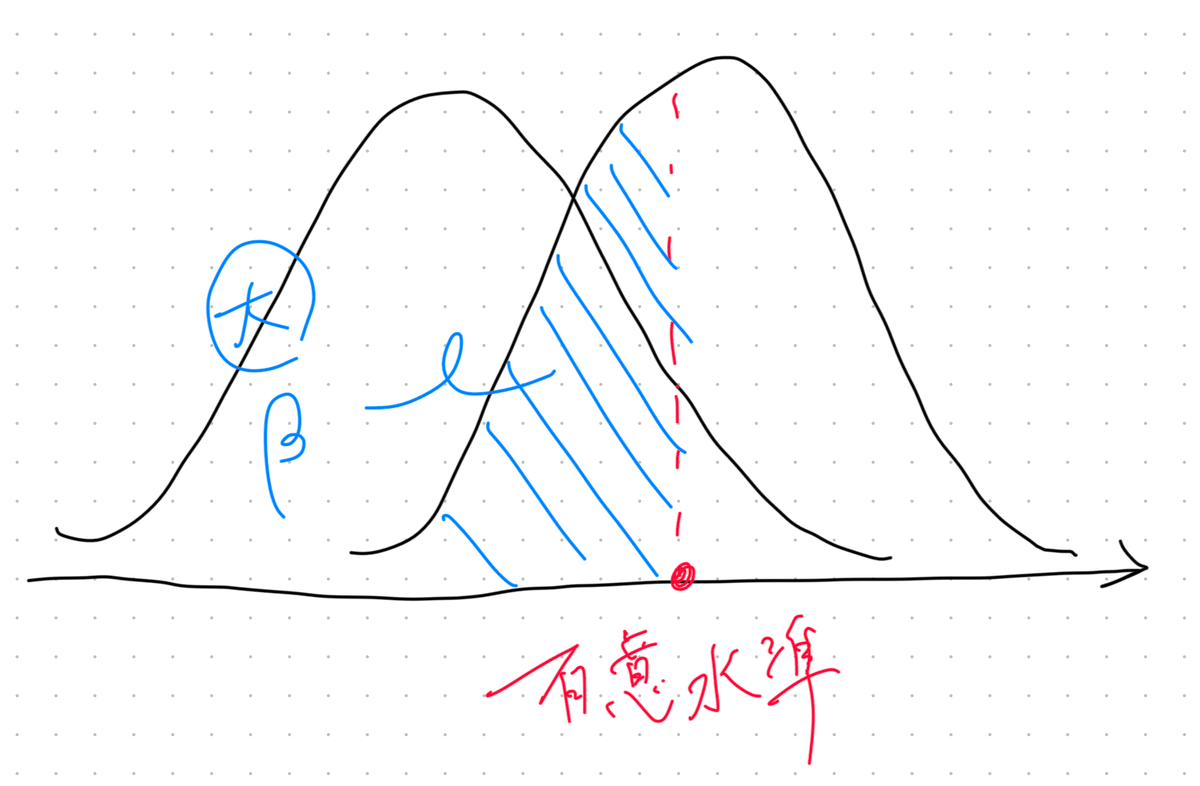
帰無仮説$${H_0}$$、対立仮説$${H_1}$$がそれぞれ正しいときの分布を描画して考える

有意差がないのにあるといってしまう確率、つまり仮説検定における棄却域と同じ

第1種の過誤は有意差がない（＝帰無仮説が正しい（左の分布））にも関わらず、有意水準を超える検定統計量を取り

実現確率が$${\alpha}$$(赤斜線部分)くらい小さな確率
↓
帰無仮説の分布より対立仮説の分布に従ってるっぽい
↓
帰無仮説棄却で（帰無仮説と）有意差ある対立仮説採用

これは普段の仮説検定でやってるので慣れているだろう

有意差があるのにないといってしまう確率、つまり第1種の過誤と逆

第2種の過誤は有意差がある（＝対立仮説が正しい（右の分布））にも関わらず、棄却域$${\alpha}$$に入らなかったので帰無仮説採用してしまう確率$${\beta}$$

サンプルサイズを固定した上でこの有意水準を大きくすれば
有意水準の点が左に行き
$${\alpha}$$は増え$${\beta}$$が減るので
第1種の過誤と第2種の過誤はトレードオフになる

サンプルサイズが一定のとき第1種の過誤と第2種の過誤はトレードオフだが
サンプルサイズを大きくしたらどうなるか

ここで有意水準を一定にしたときを考えよう
当然有意水準に依存する$${\alpha}$$の値は変わらないが
「有意なときに見逃す確率」である$${\beta}$$は小さくなる

これはサンプルが増えれば増える
↓
帰無仮説と対立仮説の分布が確立
↓
分布差がはっきりするので有意なときに見逃差ない
↓
$${\beta}$$は小さくなる

と考えれば定性的に理解できるだろう

効果の差とは帰無仮説と対立仮説の分布の差のことで
エフェクトサイズとも言われる

効果の差が大きいと双方の分布が離れていくので
$${\beta}$$は小さくなることが容易にわかるだろう

これまでの考察を踏まえてサンプルサイズと効果の差の関係をまとめる

エフェクトサイズが小さいときは
双方の分布が近づくので、$${\beta}$$は大きくなる

ここで有意な時に見逃さず有意と判断する
検出力と言われる$${1 - \beta}$$の値を大きくしたい
つまり$${\beta}$$の値を小さくしたいとする

サンプルサイズを大きくすると$${\beta}$$の値を小さくなるので
下図のように$${1 - \beta}$$の値を大きくなる

つまり、エフェクトサイズが小さいほど
検出力を担保するためにサンプルサイズが多く必要になってくる

大量に製造する工場では全ての製品を検査（＝全数検査）することは難しいそこで検査の基準（有意水準みたいなもの）として不良品率を定義し、製品の一部を抜き取って検査する「抜取検査」が多く用いられる

抜取検査には生産者危険と消費者危険がある

（基準より低い不良品率なので）合格とすべきものを不合格としてしまう
　→ 慎重すぎて生産者が損をする確率（第1種の過誤）

（基準より高い不良品率なので）不合格とすべきものを合格としてしまう
　→ うっかりしていて消費者に危険が及ぶ確率（第2種の過誤）