
ヤンキーでもわかる大数の法則
大数の法則のめっちゃざっくりな説明
大数の法則をwikiで調べると下記の呪文のような
文言が現れる
でも実際にはざっくりいうと
めっちゃデータを多く集めたら
標本の平均が母平均に近づくよ!
って言ってるだけなのである
これをピカチュウで例えると
現在ゲットしているピカチュウの平均体重が8.5kg(標本平均)と少し重くても
無限にゲットして体重の平均を測ってくと
一般的なピカチュウの体重6.0kg(母平均)に限りなく近づく
ということである

現実世界に当てはめるとデータをめっちゃ集めて平均出せばより正確な値になるよ!ってこと
例えばR社の新人研修では
100枚名刺交換してくるというものがある(根性)
そこで新人が名刺交換をして応じてくれる人の確率を調べるとする
新人3名にやらせて0.5%だったとしたどう思うか?
流石にもっと高い確率だろうと思うので、もっと人数を増やしたくなるだろう
新人30人にやらせたら確率が1.4%
新人300人にやらせたら確率が0.9%
新人3000人にやらせたら確率が1.1%
となったら、名刺交換コンバージョン率が大体1.0%くらいだろうと結論づけるだろう
これは無意識に大数の法則を使っているのである
ではこれを少し数学的に証明していこう
数学的にいうと、標本平均が母平均に近づいていくということ
まずとある母集団が
母平均$${\mu}$$、標準偏差$${\sigma}$$
の正規分布に従うとする
グラフで書くとこうなる
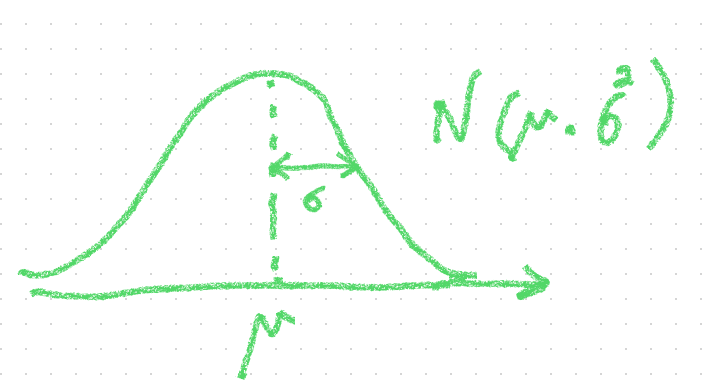
この母集団からデータを10個ランダムに取ってきて
その平均の標本平均を算出すると
その確率分布は赤線のように確率分布の幅が狭くなっている

これは標準偏差が$${\sigma}$$から$${\frac{\sigma}{\sqrt{10}}}$$
と小さくなっているからである (下記証明)
$$
Var(\bar{x}) \\
= Var(\frac{\sum_{1}^{10} x_i}{10})\\
= \frac{1}{10^2} (Var(x_1)+Var(x_1)+ \cdots + Var(x_{10}))\\
= \frac{1}{10}Var(x)\\
$$
なのでこれにルートをかけると標準偏差がもとまる
$$
\sqrt{Var(\bar{x})} \\
= \frac{\sqrt{V(x)}}{\sqrt{10}}\\
= \frac{\sqrt{\sigma^2}}{\sqrt{10}}\\
= \frac{\sigma}{\sqrt{10}}
$$
つまりデータを100個持ってきたら
標準偏差は$${\frac{\sigma}{\sqrt{100}}}$$となり
その確率分布は青線のように、さらに確率分布の幅が狭くなっている
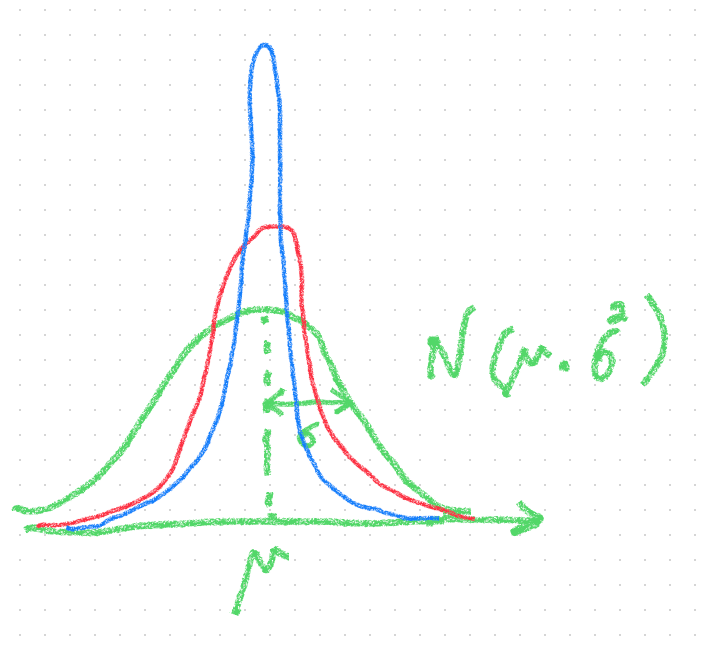
このように標本内のデータの個数を増やせば増やすほど
標本平均の確率分布の幅がどんどん狭くなっていき
母平均$${\mu}$$に近づいていく

