
統計準1級 第13章 ノンパラメトリック法 解説
本章で扱うもの
一般的に検定は以下のようなものがある
この章では、太字に記載している正規分布に関する検定を解説していく
パラメトリック検定
正規分布に関する検定(11章)
t検定
$${\chi^2}$$検定
F検定
二項分布に関する検定(12章)
母比率の(差の)検定
ポアソン分布などその他に関する検定(12章)
適合度検定
尤度比検定
ノンパラメトリック検定(13章)<----
(符号付き)順位和検定
並び替え(符号)検定
11章、12章で学んだ検定では、
母集団を正規分布や二項分布に母集団が従う仮定を置いていた
パラメトリック検定を学んでいた
しかし、特にスモールデータのときのように
母集団が特定の確率分布に従ってない時はどうしたらいいだろうか
例えばt検定を行うときに
サンプルサイズが十分に大きくなく、中心極限定理が使えなく
標本平均が正規分布に従うと仮定できないとき、、、とか
そこで本章では
母集団の仮定を置くことなくおこなえるノンパラメトリック検定
を学んでいく
以下帰無仮説を
帰無仮説:2群の分布は等しい
と考えて検定を行う
独立2群の差の検定
独立2群について考えるので
以下のような「関東と関西のお笑いスコア」例を題材にして考える

ウィルコクソンの順位和検定
ウィルコクソンの順位和検定では
以下の段階に沿って順位和から片側P値を計算していく
各群の小さい値から順位を与える
その順位和を検定統計量とし、順位和が少ない方の群の順位和以下の順位組み合わせを分子として計算
全てのの順位組み合わせを分母として計算
まず順位和を計算すると
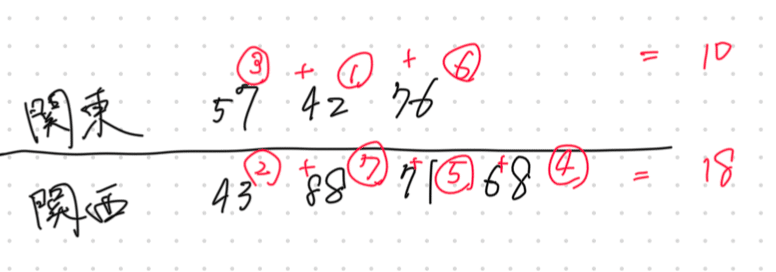
となるので、少ない方の順位和10について下記のように考える
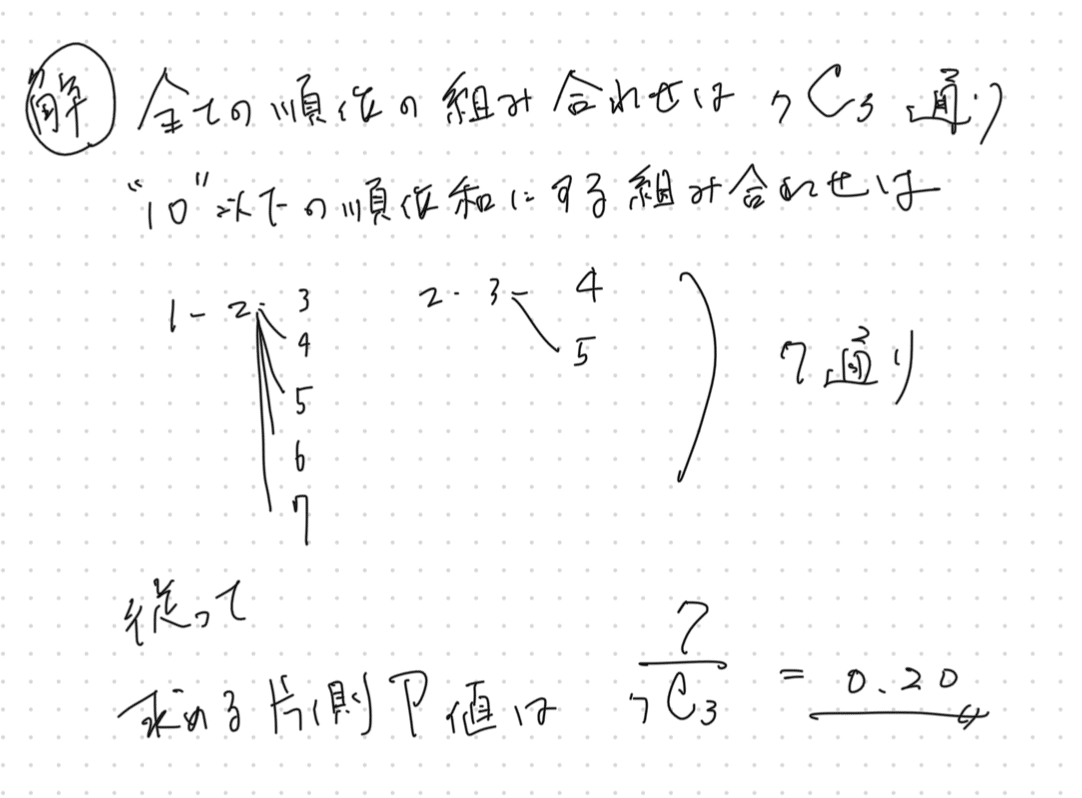
並べ替え検定
並び替え検定では
以下の段階に沿って平均値から片側P値を計算していく
各群の平均値を与える
その平均値を検定統計量とし、平均値が少ない方の群の平均値以下の組み合わせを分子として計算
全てのの組み合わせを分母として計算
まず各群の平均値を計算すると

となるので少ない方の平均値58以下について以下のように考える

対応のある2群の差の検定
対応のある2群について考えるので
以下のような「補習前と後によるテスト点数の差」例を題材にして考える

ウィルコクソンの符号付き順位検定
各群の絶対値の小さい値から符号付き順位を与える(0入れない)
その順位和の正の値を検定統計量とし、その順位和以下をとる組み合わせを分子として計算
順位和の正の値以上になるの組み合わせとして分母として計算
正の値を取っていた順位の和は15なので
これらの組み合わせと、全体の組み合わせを考えて

符号検定
各群の絶対値の小さい値から符号付き順位を与える(0入れない)
その順位和の正値の個数を検定統計量とし、その順位和の正値の個数以上になるの組み合わせを分子として計算
全ての組み合わせを分母として計算

独立3群以上の差の検定
クラスカル・ウォリス検定
各群の平均順位和$${\bar{R_i}}$$を計算する
それと各群の順位の中央値$${\bar{N}}$$との差の2乗和を計算
その2乗和に各群のサンプルサイズ$${n_i}$$をかけた和と全体のサンプルサイズ$${N}$$用いて下記のような検定統計量を計算する
$$
\begin{aligned}
T = \frac{12}{N(N + 1)} \sum_i n_i (\bar{R_i} - \bar{N})^2
\end{aligned}
$$
以下のような「3群のテスト点数」例を題材にして考える

これらの平均順位和を計算して検定統計量を求めてp値を求める

※ 対応のある3群以上の検定にはFriedman検定を用いる
