
グローバルSCMにおける生産配分・出荷計画の最適化(ナップサック問題)について
【はじめに】
本記事は、過去に掲載したSCM関連記事の続きです。
前回までの記事では、サプライチェーンの最終消費地となる各国の販売チャネルにおいて、最終需要地を起点に、モデル化した仮想のPSI計画(定期発注方式の在庫管理)を連鎖させて、供給元のマザープラントに向かって需要情報を伝達して、サプライチェーン計画を整合させるアプローチ(ここでは、Backward Planningと呼ぶことにします)をご紹介しました。
今回は、グローバル・サプライチェーンの供給元となるマザープラント側において、最終消費地から集まって来た需要情報(週次の出荷要求量)に対して、市場価値を最大化させる出荷ロット・仕向地の組合せを求めるという問題について考えてみたいと思います。
生産配分(出荷優先)の処理イメージは「図A マザープラントにおける生産配分(出荷優先)処理」のとおりです。
ここでの検討の対象範囲は、以前の記事で紹介したサプライチェーンの全体イメージに当てはめてみると「図1. マザープラントにおける生産配分・出荷優先の検討範囲」に示す赤枠の中の部分になります。
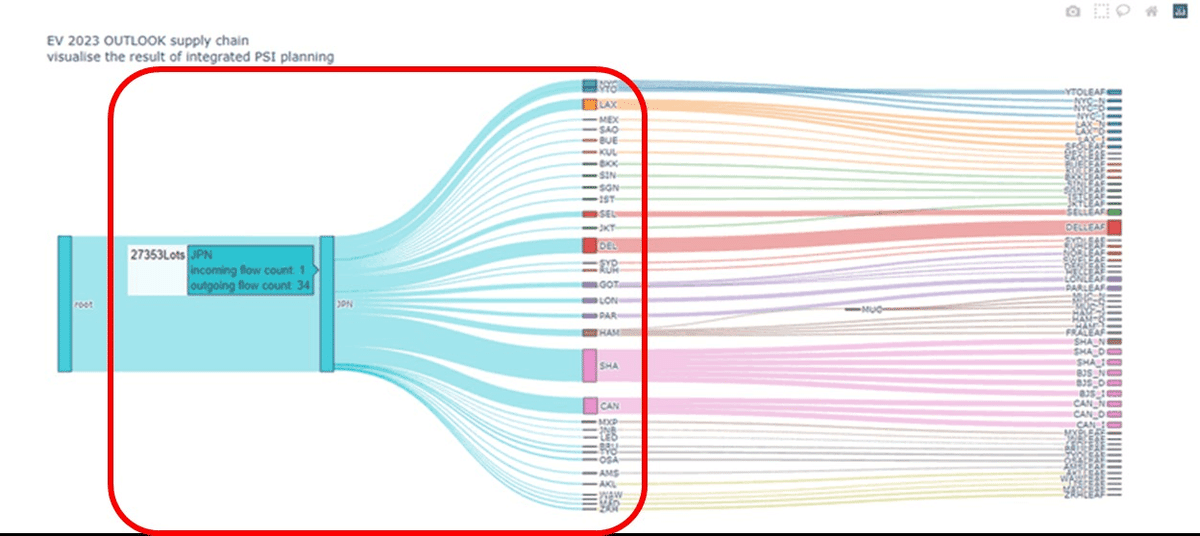
この問題は、実際の業務の観点からは、マザープラントの毎週の出荷計画における出荷優先度の決定、あるいは各仕向け地への生産配分といった問題に相当すると思います。ここでは以降、「生産配分の問題」と呼ぶことにしますが、出荷計画の優先度決定と同じと考えてよいと思います。
今回、この生産配分問題の簡易デモをpythonで実装するにあたって、どのような方法で解くのが良いか検討を進める中で、「表1. 生産配分とナップサック問題の問題特性」のとおり、問題の特性が類似している「ナップサック問題」に置き換えて解くことができるのではないかと考え、pythonの線形計画モジュール(PuLP)を使った簡単なナップサック問題のサンプルコードを参考に試作してみました。
※簡易デモのpythonのコードは、下記のgithubに公開しています。別途githubに掲載したいと思います。
Yasushi-Osugi/PySI_V0R3_mother_plant_Knapsack: PySI_V0R3 is demand plan on supply chain. and production allocation with Knapsack solver. (github.com)

pythonでの簡易デモの詳細については別途ご紹介させていただくとして、ここではまず、マザープラントの出荷時点での生産配分について、どのような処理が行われているのか、その処理の途中経過をイメージで見ていきたいと思います。
【生産配分の処理イメージ】
マザープラント側の出荷時点での生産配分の処理イメージを示したのが 「図2 マザープラントにおける生産配分・出荷優先の処理推移」です。
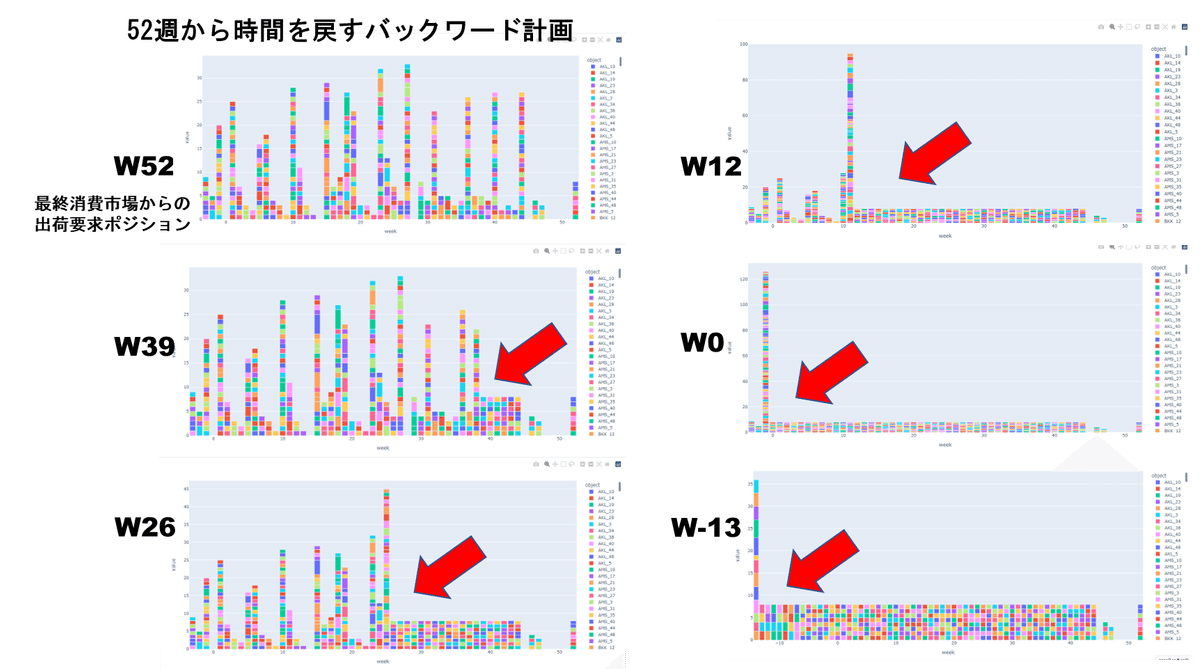
なお、実際の生産配分の処理は、ナップサック問題を解く線形計画法のモジュールに渡しているので、コンマ1秒以下で最適解を生成している部分ですが、毎週毎週の処理の様子が分かるように途中にグラフ出力処理を挟んでいます。
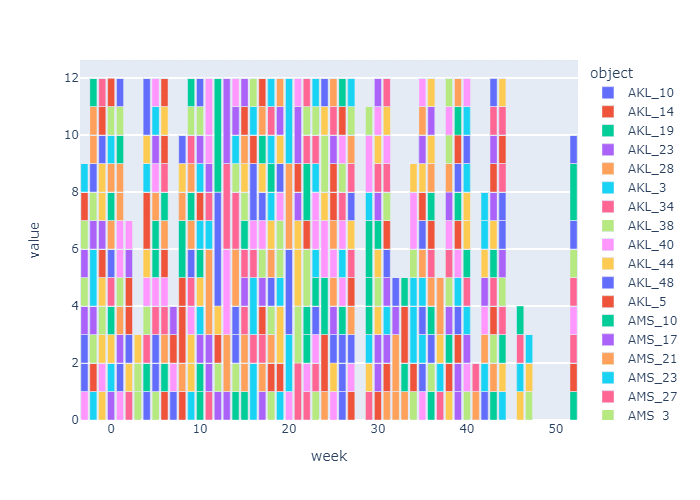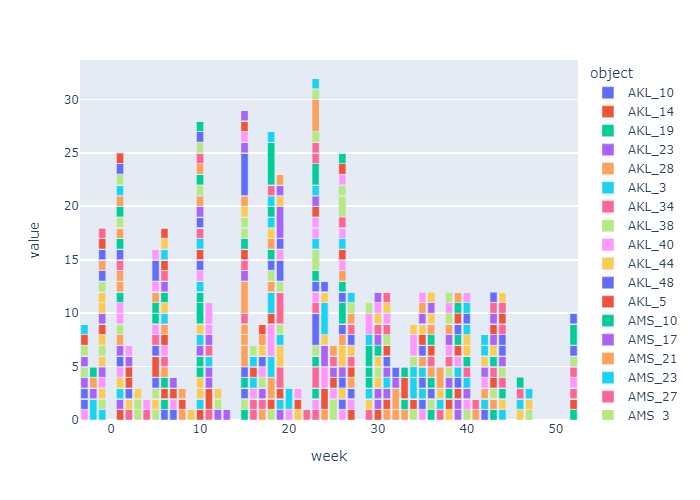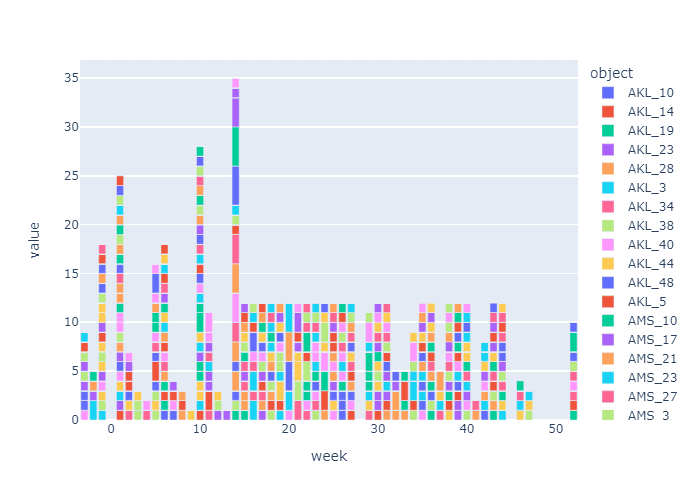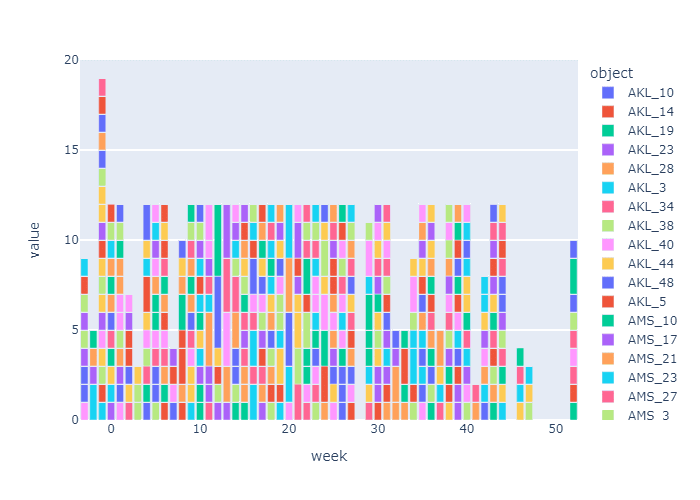
「図2. マザープラントにおける生産配分・出荷優先の処理推移」において、W52は、計画の初期状態です。生産配分の問題を週次で、52週から時間を戻る方向に、毎週毎週の生産配分問題を解いていきます。
図2では、生産配分(ナップサック)問題を週次で解いて、生産平準化している様子を、四半期(=13週)のスナップ・ショットで表示しています。
ここで、毎週の生産出荷枠から外れた出荷要求ロットは、「繰り戻し」して、前週の出荷枠に積み上がるというルールで実装しています。
図中、W39, W26, W12, W0, W-13と四半期の生産配分の途中経過を見ると、積み上がった出荷要求ロット群の中から価値を最大化するロットの組合せが選択されて、徐々に生産が平準化されていく様子が分かります。
このように、ナップサック問題を解くモジュール、knapsack solverを組み込んだ生産配分の動きをpythonの簡易デモとして実装しました。
余談になりますが、実は、以前の記事でご紹介したサプライチェーン計画では、このW52の初期状態に対して、単に「供給元(マザープラント)における生産を平準化する」という問題設定で、PSI計算に適当なパラメータを設定して生産配分の問題を処理していました。
今回は、「生産の平準化」と「市場に提供する価値を最大化する」という問題設定で、ナップサック問題に置き換えて生産配分しているので、「最重要顧客からの要請」と「自社の利益」とを考慮して価値を最大化する製品供給が行われることになります。
以下では、この生産配分問題の結果について、もう少し見ていきたいと思います。
【先行生産のスタート時期について】
供給元(マザープラント)では、例えば、2023年のグローバル需要に対応するためには、2022年の何時の時点から生産を開始するべきかという点が気になります。
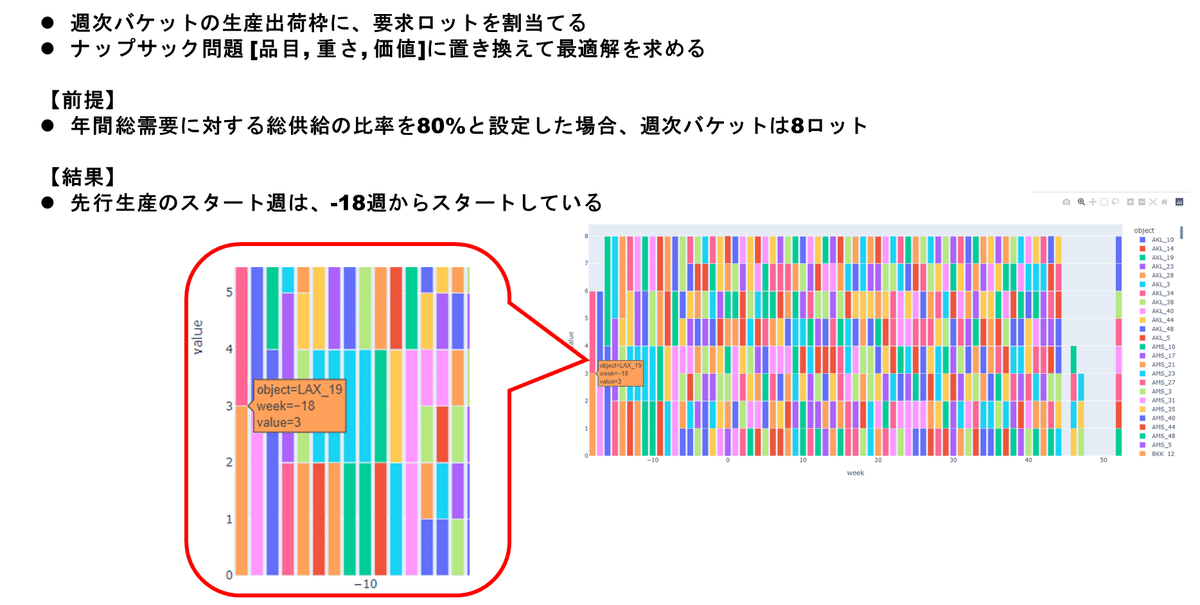
「図3. マザープラントの生産配分・優先出荷の結果」は、最終需要地に着荷する半年前、先行生産する年の26週から生産配分した結果です。
ここでは前提条件として、年間の総生産能力をグローバル総需要の80%に設定して、週次生産の能力を設定しています。この場合、先行生産のスタートは、2022年の年末52週から18週前、2022年の第34週 8月8日~8月14日の週からスタートする必要があることが分かります。
【想定されるシナリオ 在庫方針について】
供給元(マザープラント)における先行生産のスタート時期が分かると、次に問題となるのが、この先行生産の結果、発生する備蓄在庫をどこで保管するべきかという問題が浮かび上がってきます。
筆者の経験では、マザープラントの出荷ヤードにグローバル総需要に応える在庫保管を行うことは現実的ではなく、むしろ、マザープラント側では先行生産した製品でも、生産即出荷で、出荷ヤードに完成製品を滞留させない在庫方針を取る企業が多いようです。
一方で、最終需要地の前線の販売チャネルでは、例えば年末のクリスマス・シーズンの商品在庫を数か月前から在庫保管することは、保管費用や仕入れ費用が余分に発生するため考えにくく、週次や日次の納品要請に迅速に応えて、店舗に納品してくれる体制が望まれます。
結果、グローバルの域内在庫、あるいは大きな市場をかかえる国では国内の物流拠点在庫において、地域内の需要変動を吸収する保管スペースを確保して、最終需要地のリクエストに俊敏に対応する仕組み、直近の需要変化を予測しながら補充する仕組みなどを整備することになると想定されます。
このような域内在庫による商品補充の仕組みの中で、商品の売れ行きの良し悪し、商品在庫の流動の様子を供給元(マザープラント)の生産計画にフィードバックをかけることが、生産のアクセル・ブレーキをかける上で重要な判断材料になってくると思います。
ところで、以前の記事で、「海外の販売会社では、販社の出荷(=実販)情報の変化だけではなく、POSの消費情報(=実需)の動きと(販社から先の)市中在庫の流動が重要になる」というお話をしました。
つまり、グローバルSCMの在庫モデルとして、二段階(市中在庫と域内在庫)の在庫モデルを想定して、供給元(マザープラント)の需給調整を行うことはグローバル・オペレーションの実態に即していると思います。
【追記】
一方で近年、amazonや楽天などのネット販売、メーカーやファッションブランドなどの自社通販のように、市中在庫を排除して、消費者一人一人の個人のスマホからの注文(実需)が、域内や国内の物流拠点の在庫にダイレクトに引当られて、出荷配送指示に直結しているビジネスモデルが増えています。
EV、電気自動車のネット販売もその一つですが、完成品が市場に流れるアウトバウンド・サプライチェーンにおいては、グローバルに一段階の在庫(域内在庫)モデルで管理される商品が今後、増えていくと思います。
以上から、次のような取り組み仮説を定義することができます。
【グローバルSCMの供給元(マザープラント)における需給調整の仮説】
最前線の店舗のPOS情報を日々収集して、店舗ごとの日々の消費スピードなどから、実需の変化を予測するとともに、サプライチェーン上の中間在庫として、一段階または二段階の在庫、「市中在庫」または「域内在庫」の流動をシミュレーションすることで、マザープラントにおける製品生産のアクセル・ブレーキ、生産配分(仕向地)の変更など、需給調整の判断を的確に行うことができる。
少し大きな仮説を定義してしまいました。
ただ、問題の全体を把握するという点では、このようなサプライチェーンの全体イメージを持ちながら、グローバルSCMの中の個々の問題に入っていくのが良いのではないかと思います。
次回は、上記の「需給調整の仮説」を構成するいくつかの部分問題の中でも中心的な機能と思われる「生産配分の機能」について、python で実装した簡易デモの詳細を見ていきたいと思います。
ポイントは、サプライチェーンの供給システムを設計する立場からは、需要特性に応じた生産能力の上限と変化幅、中間在庫拠点の在庫バッファーを設定する際の考え方になると思います。
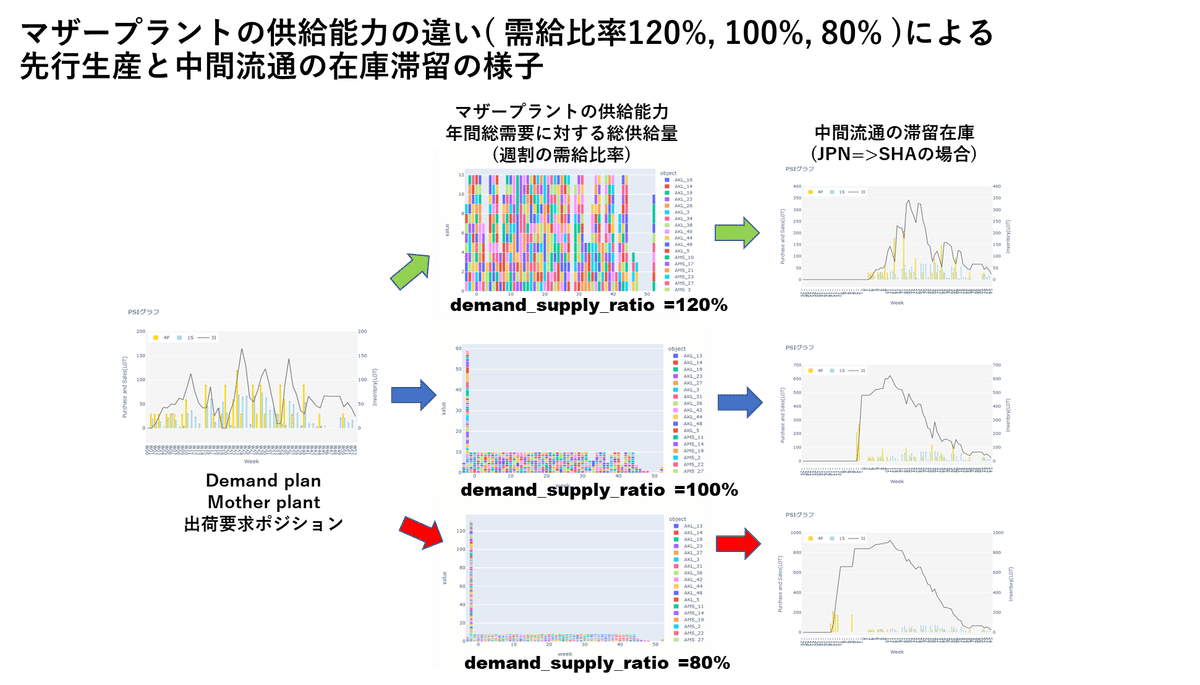
ご紹介してきた生産配分の結果から「図4. マザープラントの供給能力と中間流通の在庫滞留の関係」のように、出荷・流通の在庫変動の様子を可視化することができます。図4では、年間総需要に対して、マザープラントの総供給量が十分にある(120%)場合、等しい(100%)場合、 総供給量が不足している(80%)場合について、それぞれの需給比率=120%, 100%, 80%に対して、流通側の中間在庫(ここでは日本のマザープラントから上海の国内中間在庫の部分をビックアップ)がどのように在庫滞留を発生するのかをPSI計算でシミュレーションして、PSIグラフ表示しています。
また、ITシステムの実装の立場からは、まず「図5. サプライチェーン計画のBackward planとForward planの立案処理(仮説)」のようなサプライチェーン計画の処理の全体像を仮定した上で、サプライチェーン全体に共通する「共通計画単位」common plan unit(注1)を使って、生産配分をナップサック問題(線形計画法)で解くために必要な入力データ
●ナップサックの容量制約
●詰め込む品物の品名、数量、価値
を生成する際の考え方について、もう少し詳しく見ていきたいと思います。

(注1)前回までの記事で、PSI計画の連携デモで生成された約20万件の発注オーダー・ロット、「共通計画単位」common plan unitが生成されているので、これを使って生産配分問題を解きます。
