
『医学のための因果推論』のための統計学入門:10.正規線型モデル
『医学のための因果推論Ⅰ 一般化線形モデル』を勉強した時のまとめです。
結構難しい本でしたので自分なりの解釈を入れながらまとめました。
ここではベースライン値があるランダム化臨床試験におけるコントロール群の必要性や、共変量調整の意義について説明します。
また残差プロットが非線型によるモデルの誤特定を防ぐために有用であることを示します
正規線型モデルの構造
アウトカム変数 $${Y_i \ (i=1, \ldots, N)}$$ が、それぞれ異なる平均を持つ独立な正規分布に従うと仮定します。
このとき、平均 $${\mu_i}$$ と共変量 $${X_1, X_2, \ldots, X_p}$$ は恒等リンク関数を介して線型の関係にあります。
このモデルは、以下のように数式で表されます。
$$
\begin{aligned} Y_i &\sim N\left(\mu_i, \sigma^2\right) \\ \mathrm{E}\left(Y_i \mid \boldsymbol{X}_i\right) &= \mu_i = \boldsymbol{X}_i \boldsymbol{\beta} \end{aligned}
$$
ここで、
$${Y_i}$$:アウトカム変数
$${\boldsymbol{X}_i}$$:共変量のベクトル
$${\boldsymbol{\beta}}$$:回帰係数のベクトル
$${\sigma^2}$$:分散(共通)
このモデルは一般化線型モデルの一種であり、従来の分散分析や回帰分析もこのモデルに含まれます。
正規線型モデルの推定
正規線型モデルの対数尤度関数は以下のように表されます。
$$
l(\boldsymbol{\beta}, \sigma) = \sum_{i=1}^N -\frac{1}{2} \left( \frac{y_i - \boldsymbol{X}_i \boldsymbol{\beta}}{\sigma} \right)^2
$$
これは各データ点における観測値 $${y_i}$$ と予測値 $${\boldsymbol{X}_i \boldsymbol{\beta}}$$ の差の二乗和であり、対数尤度を最大化する操作は最小二乗法で解を求める計算と同じです。
最尤推定量の導出
対数尤度を最大化することで、最尤推定量 $${\widehat{\boldsymbol{\beta}}}$$ を求めます。
逆行列が存在する場合、以下の明示的な解が得られます。
$$
\widehat{\boldsymbol{\beta}} = \left( \boldsymbol{X}^\top \boldsymbol{X} \right)^{-1} \boldsymbol{X}^\top \boldsymbol{Y}
$$
$${\boldsymbol{X}}$$:デザイン行列(各行が $\boldsymbol{X}_i$)
$${\boldsymbol{Y}}$$:アウトカムのベクトル
分散の推定
分散 $${\sigma^2}$$ の推定は、以下の式を用いることが一般的です。
$$
\widehat{\sigma}^2 = \frac{1}{N - p - 1} (\boldsymbol{Y} - \boldsymbol{X} \widehat{\boldsymbol{\beta}})^\top (\boldsymbol{Y} - \boldsymbol{X} \widehat{\boldsymbol{\beta}})
$$
$${p}$$は説明変数の数です。
最尤推定量の性質
正規線型モデルにおいて、最尤推定量 $${\widehat{\boldsymbol{\beta}}}$$ は以下のような漸近正規性を持ちます。
$$
\widehat{\boldsymbol{\beta}} \xrightarrow{d} N\left( \boldsymbol{\beta}, \sigma^2 \left( \boldsymbol{X}^\top \boldsymbol{X} \right)^{-1} \right)
$$
また、小標本の場合でも不偏性が成り立ちます。
$$
\mathrm{E}(\widehat{\boldsymbol{\beta}}) = \boldsymbol{\beta}
$$
データの非線型性によるモデルの誤特定
正規線型モデルは臨床検査で得られる測定値、例えば糸球体濾過率や血圧などの統計解析に広く用いられています。
Brochner-Mortensen et al. (1977) は、男性180人と女性200人を対象に、血漿クレアチニン濃度と糸球体濾過率の関係を調べました。
表11-1は、ランダムに選ばれた31人のデータです。

import pandas as pd
import matplotlib.pyplot as plt
# 表11-1のデータを手動で入力
data = {
'Subject': list(range(1, 32)),
'GFR (mL/min)': [90, 45, 103, 100, 93, 90, 70, 77, 47, 45, 60, 53, 35, 63, 55, 35,
38, 47, 45, 40, 27, 37, 25, 15, 20, 10, 5, 5, 5, 10, 12],
'Creatinine (mg/dL)': [0.85, 0.99, 1.13, 1.13, 1.13, 1.13, 1.13, 1.27, 1.41, 1.47,
1.47, 1.56, 1.69, 1.7, 1.75, 1.75, 1.83, 1.98, 2.03, 2.09,
2.77, 2.96, 3.11, 3.96, 4.69, 4.8, 5.93, 5.93, 5.93, 7.79, 11.02]
}
df = pd.DataFrame(data)
# 表示のためのフォーマット設定
fig, ax = plt.subplots(figsize=(10, 6))
ax.axis('off')
ax.axis('tight')
table = ax.table(cellText=df.values, colLabels=df.columns, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.auto_set_column_width(col=list(range(len(df.columns))))
plt.show()
図11-1はこのデータから描いた散布図です。

import matplotlib.pyplot as plt
plt.scatter(df['Creatinine'], df['GFR'])
plt.xlabel('Creatinine Concentration (mg/dL)')
plt.ylabel('Glomerular Filtration Rate (mL/min)')
plt.title('Figure 11-1 Left Top: Scatter Plot of Creatinine vs GFR')
plt.show()線形モデル
クレアチニン濃度を $${X_i}$$、糸球体濾過率を $${Y_i}$$ とすると、$${X_i}$$画像化すると $${Y_i}$$が減少していく関係が見られます。
最小二乗法により、線形モデル
$$
\mathrm{E}\left( Y_i \mid X_i \right) = \beta_0 + \beta_1 X_i
$$
を当てはめると、以下の推定値が得られます。
$$
\widehat{\beta}_0 = 71.1, \quad \widehat{\beta}_1 = -9.0
$$
図11-2は、この直線を散布図に重ねたものです。

# 説明変数と目的変数
X = df[['Creatinine']]
y = df['GFR']
# 線形回帰モデルの当てはめ
linear_model = LinearRegression()
linear_model.fit(X, y)
# 回帰直線のプロット
plt.scatter(df['Creatinine'], df['GFR'], label='Data')
plt.plot(df['Creatinine'], linear_model.predict(X), color='red', label='Linear Fit')
plt.xlabel('Creatinine (mg/dL)')
plt.ylabel('Glomerular Filtration Rate (mL/min)')
plt.title('Linear Regression Fit')
plt.legend()
plt.show()
# 回帰係数の表示
beta_0 = linear_model.intercept_
beta_1 = linear_model.coef_[0]
print(f'Linear Model: y = {beta_0:.2f} + {beta_1:.2f}x')残差プロットによる線形モデルの検討
この線形モデルがデータによく当てはまっているかを検討するために、残差プロットを作成します。
残差が小さいほど、モデルの予測が観測データに近く、モデルがデータにうまく当てはまっていることを示します。
横軸に説明変数を取ることで説明変数の水準ごとに残差のパターンが見られ、モデルの適合度に関する情報を得ることができます。
残差に一定の傾向やパターンが見られる場合、モデルが正確に当てはまっていない可能性があります。
線形回帰モデルでは説明変数と目的変数の間に線型関係があると仮定します。
この線型性の仮定を検証するために残差プロットを用います。
理想的なモデルでは残差はランダムに散らばり、横軸に対して一定のパターンを示さないことが期待されます。
残差が平均してゼロの周りに分布していると、予測値が全体的に偏りなく観測値を再現していると考えることができます。
また、特定のパターンがなくランダムに散らばっていることは、説明変数と残差に相関がないことを示しており、モデルがデータの特徴を十分に捉えていることを示唆します。
図11-3は、横軸に $${X_i}$$、縦軸に残差 $${Y_i - \widehat{\mathrm{E}}\left( Y_i \mid X_i \right)}$$ をとったものです。

# 残差の計算
residuals = y - linear_model.predict(X)
# 残差プロット
plt.scatter(df['Creatinine'], residuals)
plt.axhline(y=0, color='red', linestyle='--')
plt.xlabel('Creatinine (mg/dL)')
plt.ylabel('Residuals')
plt.title('Residual Plot for Linear Model')
plt.show()残差プロットを見ると、残差とクレアチニン濃度の間にU字型の傾向が見られます。
U字型の傾向は、説明変数(クレアチニン濃度)と目的変数(糸球体濾過率)の関係が線型ではなく非線型であることを示唆しています。
つまりモデルがデータの実際の傾向を捉えきれておらず、モデルの線型性(linearity)の仮定が誤っていることを示しています。
逆数モデル
クレアチニンは筋肉で代謝されたクレアチンから生成される副産物です。
クレアチニンの生成速度は通常筋肉量や代謝によって決まるため、比較的安定しています。
クレアチニンは腎臓の糸球体と呼ばれる濾過装置を通じて尿中に排泄され、ほとんどが糸球体で濾過されます。
通常クレアチニンは腎臓での再吸収や分解をほとんど受けないため、クレアチニン濃度は腎機能の指標として利用されます。
腎臓の糸球体濾過率が正常である場合、クレアチニンは効率的に尿中に排泄され、血中のクレアチニン濃度は低くなります。
しかし糸球体濾過率が低下すると腎臓のろ過能力が低下し、血中に残るクレアチニンの量が増えるため、血清クレアチニン濃度が上昇します。
上記のように考えると、糸球体濾過率と血中クレアチニン濃度の関係は反比例の関係にあることが予想されます。
つまり以下のようなモデルがより適切です。
$$
\mathrm{E}\left( Y_i \mid X_i \right) = \beta_0 + \frac{\beta_1}{X_i}
$$
このモデルを当てはめるために、クレアチニン濃度の逆数 $${1 / X_i}$$ を計算し、それを説明変数として最小二乗法を行います。
その結果、以下の推定値が得られます。
$$
\widehat{\beta}_0 = -2.5, \quad \widehat{\beta}_1 = 88.3
$$
図11-4は、この逆数モデルを散布図に重ねたものです。

# 逆数を説明変数として追加
df['Creatinine_inv'] = 1 / df['Creatinine']
X_inv = df[['Creatinine_inv']]
# 逆数モデルの当てはめ
reciprocal_model = LinearRegression()
reciprocal_model.fit(X_inv, y)
# 逆数モデルのプロット
plt.scatter(df['Creatinine'], df['GFR'], label='Data')
plt.plot(df['Creatinine'], reciprocal_model.predict(X_inv), color='green', label='Reciprocal Fit')
plt.xlabel('Creatinine (mg/dL)')
plt.ylabel('Glomerular Filtration Rate (mL/min)')
plt.title('Reciprocal Model Fit')
plt.legend()
plt.show()
# 回帰係数の表示
beta_0_inv = reciprocal_model.intercept_
beta_1_inv = reciprocal_model.coef_[0]
print(f'Reciprocal Model: y = {beta_0_inv:.2f} + {beta_1_inv:.2f}/x')逆数モデルを用いることで、データへの当てはまりが改善していることがわかります。

# 逆数モデルの残差
residuals_inv = y - reciprocal_model.predict(X_inv)
# 逆数モデルの残差プロット
plt.scatter(df['Creatinine'], residuals_inv)
plt.axhline(y=0, color='red', linestyle='--')
plt.xlabel('Creatinine (mg/dL)')
plt.ylabel('Residuals')
plt.title('Residual Plot for Reciprocal Model')
plt.show()モデルのAIC比較
一次関数モデルと逆数モデルの当てはまりを客観的に比較するために、AIC(赤池情報量基準)を用います。
一次関数モデルのAIC:188.82
逆数モデルのAIC:163.24
import math
# AICの計算関数
def calculate_aic(n, rss, k):
return n * math.log(rss / n) + 2 * k
# 残差平方和(RSS)の計算
rss_linear = sum(residuals ** 2)
rss_inv = sum(residuals_inv ** 2)
n = len(df)
k = 2 # β₀とβ₁
# AICの計算
aic_linear = calculate_aic(n, rss_linear, k)
aic_inv = calculate_aic(n, rss_inv, k)
print(f'Linear Model AIC: {aic_linear:.2f}')
print(f'Reciprocal Model AIC: {aic_inv:.2f}')AICは値が小さいほどモデルの適合度が高いと評価されるため、逆数モデルを選択すべきであることがわかります。
ベースライン値のある臨床試験の解析
臨床試験でベースライン値(治療前の測定値)をどのように扱うかについて考えます。
表11-2は、アルブミン尿を呈する1型糖尿病・高血圧患者16人を対象に、カプトプリルまたはプラセボをランダムに割り付けた臨床試験のデータです(Hommel et al., 1986)。

# 表11-2のデータ
data_11_2 = {
'Treatment': ['Captopril'] * 9 + ['Placebo'] * 7,
'Baseline SBP (mmHg)': [147, 129, 158, 164, 134, 155, 151, 144, 153,
133, 129, 152, 161, 154, 141, 156],
'SBP at 1 Week (mmHg)': [137, 120, 141, 137, 140, 144, 134, 143, 142,
139, 134, 136, 151, 147, 137, 149]
}
df_11_2_english = pd.DataFrame(data_11_2)
# 表示のためのフォーマット設定
fig, ax = plt.subplots(figsize=(10, 4))
ax.axis('off')
ax.axis('tight')
table = ax.table(cellText=df_11_2_english.values, colLabels=df_11_2_english.columns, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.auto_set_column_width(col=list(range(len(df_11_2_english.columns))))
plt.title("Table 11-2 Antihypertensive Clinical Trial Data", pad=20, fontsize=14)
plt.show()この論文では、カプトプリル群9人は治療開始1週目の収縮期血圧がベースライン値に比べて有意に低下し(対応のあるt検定、p < 0.01)、プラセボ群7人では有意な変化がなかった(p = 0.17)ため、カプトプリルは有効であると述べられています。
しかし、この結論は正しいでしょうか。
平均への回帰とコントロール群の必要性
このようなベースライン値のあるランダム化臨床試験では、治療前後の変化量をアウトカムにすることができます。
しかし、ベースラインから有意な変化があったかどうかを主たる解析にすべきではありません。
平均への回帰(regression to the mean)という現象が存在するためです。
平均への回帰とは、特に極端な値(非常に高いまたは低い値)が観測された場合、その後の測定では平均に近づく傾向がある現象を指します。
例えばIQが高い人同士が子供を成したとしても、その次の世代は平均的なIQに近づく確率の方が高くなります。
このように、平均への回帰はランダムな変動が伴うデータで一般的に見られるものです。
今回のケースでは、たとえば血圧が非常に高い状態の患者が治療を受け、その後測定された血圧が少し低下した場合、それが治療の効果なのか、単に平均への回帰による変化なのかが曖昧になります。
極端な値をもつ被験者は治療なしでも平均に近づく傾向があるため、「治療群で測定値が変化した」という結果だけでは不十分であり、コントロール群と比較して治療による特別なな効果があったかどうかを確認することが必要です。
これにより、自然変動による変化と治療効果を区別できます。
モデル構築
治療後の測定値のみをアウトカムとした場合
いっぽうベースライン値を用いず、治療後の測定値のみをアウトカムとするモデルは以下の通りです。
$$
\mathrm{E}\left( \text{治療後の収縮期血圧} \mid \text{治療群} \right) = \text{切片} + \text{治療効果}
$$
このとき、データ行列は次のようになります。
$$
\boldsymbol{Y} = \begin{pmatrix} 137 \\ \vdots \\ 142 \\ 139 \\ \vdots \\ 149 \end{pmatrix}, \quad \boldsymbol{X} = \begin{pmatrix} 1 & 1 \\ \vdots & \vdots \\ 1 & 1 \\ 1 & 0 \\ \vdots & \vdots \\ 1 & 0 \end{pmatrix}
$$
治療前後の変化量をアウトカムとした場合
いっぽう治療前後の変化量をアウトカムとした正規線型モデルは以下のように表されます。
$$
\mathrm{E}\left( \text{治療前後の変化量} \mid \text{治療群} \right) = \text{切片} + \text{治療効果}
$$
このとき、データ行列は次のようになります。
$$
\boldsymbol{Y} = \begin{pmatrix} 137 - 147 \\ \vdots \\ 142 - 153 \\ 139 - 133 \\ \vdots \\ 149 - 156 \end{pmatrix}, \quad \boldsymbol{X} = \begin{pmatrix} 1 & 1 \\ \vdots & \vdots \\ 1 & 1 \\ 1 & 0 \\ \vdots & \vdots \\ 1 & 0 \end{pmatrix}
$$
変化量モデルの有効性
変化量のモデルがベースライン値を用いない解析より優れているのは、治療前後の測定値間の相関が高い場合です。
これを分散の観点から検討します。
ベースライン値の分散:$${\sigma_0^2}$$
治療後の測定値の分散:$${\sigma_1^2}$$
変化量の分散:$${\sigma_2^2}$$
ベースライン値と治療後の測定値の相関係数:$${\rho}$$
と置いたとき、変化量の分散は確率変数の和の分散ですから、$${\rho \sigma_0 \sigma_1}$$をベースラインと治療後の測定値の相関に基づいた補正項とすると、 $${\sigma_2^2}$$は以下のようになります。
$$
\begin{aligned} \sigma_2^2 &= \sigma_0^2 + \sigma_1^2 - 2 \rho \sigma_0 \sigma_1 \\ &= \sigma_1^2 \left( \left( \frac{\sigma_0}{\sigma_1} \right)^2 + 1 - 2 \rho \frac{\sigma_0}{\sigma_1} \right) \end{aligned}
$$
変化量の解析では、治療前後の差(変化量)をアウトカムとして取り扱います。
変化量の分散が小さいほど治療効果を測定する際のばらつきが少なくなり、統計的な検出力が向上します。
そのため、変化量のモデルが効果的かどうかは変化量の分散 $${\sigma_2^2}$$ が治療後の測定値の分散 $${\sigma_1^2}$$ よりも小さいかどうかで判断することが可能です。
$$
\sigma_2^2 < \sigma_1^2
$$
この不等式を変形すると、次の条件が得られます。
$$
\sigma_0^2 + \sigma_1^2 - 2 \rho \sigma_0 \sigma_1 < \sigma_1^2
$$
これをさらに整理すると、次のようになります:
$$
\sigma_0^2 - 2 \rho \sigma_0 \sigma_1 < 0
$$
両辺を $${\sigma_1^2}$$ で割ると、$${\rho > \frac{\sigma_0}{2 \sigma_1}}$$ という条件が導かれます。
この条件から、以下のような事柄を導くことができます。
分散が等しい場合($${\sigma_0^2 = \sigma_1^2}$$)
このとき、相関係数$${\rho}$$ が0.5より大きければ、変化量のモデルは有効であると判断できます。分散が等しくない場合($${\sigma_0^2 \neq \sigma_1^2}$$)
このとき、相関係数 $${\rho}$$ が $${\frac{\sigma_0}{2 \sigma_1}}$$ より大きいときに、変化量のモデルが有効になります。
2-A. ベースラインの分散が治療後の分散より小さい場合($${\sigma_0 < \sigma_1}$$)
このとき、相関係数のしきい値 $${\frac{\sigma_0}{2 \sigma_1}}$$は0.5未満になります。
つまり相関が0.5より小さくても、変化量モデルが有効となる場合があります。
直感的には、治療後の測定値の方がばらつきが大きい(治療後の影響に大きく個人差が出る)場合、変化量モデルを用いることで治療効果に関係ないばらつきを減らす効果があると考えられます。
2-B. ベースラインの分散が治療後の分散より大きい場合($${\sigma_0 > \sigma_1}$$)
このとき、相関係数のしきい値は0.5よりも大きくなります。
したがって相関がかなり強くないと変化量モデルは有効になりません
これは、治療後の測定値よりもベースラインの測定値の方がばらつきが大きい(個人差が大きい)場合、変化量モデルを用いることでばらつきが十分に減らせないことを意味します。
ベースライン値を共変量として調整した場合(共分散分析)
ベースライン値を共変量としてモデルに含めることもできます。
これは一般的に共分散分析(analysis of covariance)と呼ばれます。
$$
\mathrm{E}\left( \text{治療後の収縮期血圧} \mid \text{治療群}, \text{ベースライン値} \right) = \text{切片} + \text{治療効果} + \text{ベースライン効果}
$$
臨床試験の文脈では、ベースライン値を共変量としてモデルに含める解析のことを共変量調整(covariate adjustment)と呼びます。
このとき、データ行列は次のようになります。
$$
\boldsymbol{Y} = \begin{pmatrix} 137 \\ \vdots \\ 142 \\ 139 \\ \vdots \\ 149 \end{pmatrix}, \quad \boldsymbol{X} = \begin{pmatrix} 1 & 1 & 147 \\ \vdots & \vdots & \vdots \\ 1 & 1 & 153 \\ 1 & 0 & 133 \\ \vdots & \vdots & \vdots \\ 1 & 0 & 156 \end{pmatrix}
$$
共変量調整の主な目的は、共変量(ベースライン測定値)が目的変数の分散を説明する部分を増やすことです。
ベースライン測定値と治療後の測定値が強い相関を持つ場合、共変量としてベースライン測定値を取り入れることで、目的変数の分散の一部を共変量で説明できるため、残りの誤差項の分散が小さくなることが期待されます。
治療効果を持つ項$${\beta_1 \times \text{治療群}}$$は、治療を受けた群と受けていない群の平均の差に関する項です。
この項の分散は治療群とコントロール群の構成によって決まりますが、モデルの分散全体には影響を及ぼしません。
したがって、この項自体がモデル全体の分散の大きさに直接寄与するわけではないと考えられます。
従って、共変量としてベースライン測定値を追加したとき、治療後の測定値の分散は次のように表されます。
$$
\text{Var}(\text{治療後の測定値}) = \beta_2^2 \text{Var}(\text{ベースライン測定値}) + \text{Var}(\epsilon)
$$
ここで、$${\beta_2^2 \text{Var}(\text{ベースライン測定値})}$$はモデル全体の分散のうち、ベースライン測定値を用いて説明できる部分です。
これらの前提において、ベースライン測定値と治療後の測定値の相関$${/rho}$$と分散の比率($${\sigma_0^2 / \sigma_1^2}$$)が共変量調整の効果にどのように影響するのかをもう一度確認します。
ベースライン測定値と治療後の測定値の相関の影響
相関が高い場合($${\rho \to 1}$$)
ベースライン測定値と治療後の測定値の相関が高い場合、共変量としてのベースライン測定値によって治療後の測定値の分散の多くを説明できるため、共変量調整によって残差分散が大きく減少します。
この場合共変量調整の効果は高く、治療効果($${\beta_1}$$)の推定が精度良く行えることが期待できます。相関が低い場合($${\rho \to 0}$$)
ベースライン測定値と治療後の測定値の相関が低い場合、共変量は目的変数の分散をあまり説明できないため、共変量調整の効果は限定的です。
この場合誤差項の分散はあまり減少せず、治療効果の推定精度もあまり改善されません。
分散の比率($${\sigma_0^2 / \sigma_1^2}$$)の影響
ベースラインと治療後の測定値の分散比率も共変量調整の有効性に影響を与えます。ベースラインの分散が治療後の分散より小さい場合($${ \sigma_0^2 < \sigma_1^2}$$)
治療後の測定値のばらつきが大きいため、ベースラインを用いることでばらつきを抑える効果が期待でき、共変量調整の効果がより顕著になります。ベースラインの分散が治療後の分散より大きい場合($${\sigma_0^2 > \sigma_1^2}$$)
ベースラインのばらつきが大きいため、ベースラインを共変量として含めてもばらつきを抑える効果は限定的であり、共変量調整の効果も限定的になります。
なお、ここでの共変量調整は推定精度や検出力の向上が目的であり、バイアスの排除が目的ではありません。
解析結果の比較
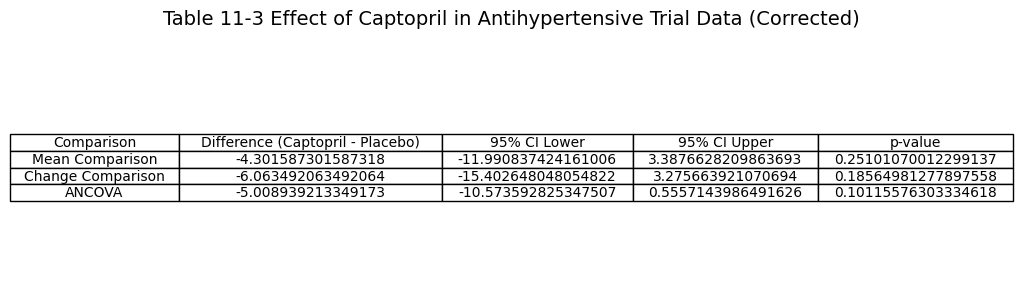
表11-3に、上記の3つのモデルで解析した結果を示します。
このデータではベースライン値と治療後の測定値の相関係数は0.60であり、ベースライン値を用いることで検出力の上昇が期待できます。
import pandas as pd
import numpy as np
import statsmodels.api as sm
from scipy import stats
import matplotlib.pyplot as plt
# 表11-2のデータ
data_11_2_corrected = {
'Treatment': ['Captopril'] * 9 + ['Placebo'] * 7,
'Baseline SBP': [147, 129, 158, 164, 134, 155, 151, 144, 153,
133, 129, 152, 161, 154, 141, 156],
'SBP at 1 Week': [137, 120, 141, 137, 140, 144, 134, 143, 142,
139, 134, 136, 151, 147, 137, 149]
}
df_11_2_corrected = pd.DataFrame(data_11_2_corrected)
# カプトプリル群とプラセボ群に分ける
captopril_corrected = df_11_2_corrected[df_11_2_corrected['Treatment'] == 'Captopril']
placebo_corrected = df_11_2_corrected[df_11_2_corrected['Treatment'] == 'Placebo']
# 1. 平均の比較
mean_diff_corrected = captopril_corrected['SBP at 1 Week'].mean() - placebo_corrected['SBP at 1 Week'].mean()
mean_se_corrected = np.sqrt(captopril_corrected['SBP at 1 Week'].var()/len(captopril_corrected) + placebo_corrected['SBP at 1 Week'].var()/len(placebo_corrected))
mean_ci_corrected = stats.t.interval(0.95, len(captopril_corrected) + len(placebo_corrected) - 2, loc=mean_diff_corrected, scale=mean_se_corrected)
mean_p_corrected = stats.ttest_ind(captopril_corrected['SBP at 1 Week'], placebo_corrected['SBP at 1 Week'], equal_var=False).pvalue
# 2. 変化量の比較
captopril_change_corrected = captopril_corrected['SBP at 1 Week'] - captopril_corrected['Baseline SBP']
placebo_change_corrected = placebo_corrected['SBP at 1 Week'] - placebo_corrected['Baseline SBP']
change_diff_corrected = captopril_change_corrected.mean() - placebo_change_corrected.mean()
change_se_corrected = np.sqrt(captopril_change_corrected.var()/len(captopril_change_corrected) + placebo_change_corrected.var()/len(placebo_change_corrected))
change_ci_corrected = stats.t.interval(0.95, len(captopril_change_corrected) + len(placebo_change_corrected) - 2, loc=change_diff_corrected, scale=change_se_corrected)
change_p_corrected = stats.ttest_ind(captopril_change_corrected, placebo_change_corrected, equal_var=False).pvalue
# 3. 共分散分析(ANCOVA)
df_11_2_corrected['Treatment_binary'] = df_11_2_corrected['Treatment'].apply(lambda x: 1 if x == 'Captopril' else 0)
X_corrected = sm.add_constant(df_11_2_corrected[['Treatment_binary', 'Baseline SBP']])
y_corrected = df_11_2_corrected['SBP at 1 Week']
model_corrected = sm.OLS(y_corrected, X_corrected).fit()
ancova_diff_corrected = model_corrected.params['Treatment_binary']
ancova_se_corrected = model_corrected.bse['Treatment_binary']
ancova_ci_corrected = (ancova_diff_corrected - 1.96 * ancova_se_corrected, ancova_diff_corrected + 1.96 * ancova_se_corrected)
ancova_p_corrected = model_corrected.pvalues['Treatment_binary']
# 結果をデータフレームにまとめる
results_corrected = pd.DataFrame({
'Comparison': ['Mean Comparison', 'Change Comparison', 'ANCOVA'],
'Difference (Captopril - Placebo)': [mean_diff_corrected, change_diff_corrected, ancova_diff_corrected],
'95% CI Lower': [mean_ci_corrected[0], change_ci_corrected[0], ancova_ci_corrected[0]],
'95% CI Upper': [mean_ci_corrected[1], change_ci_corrected[1], ancova_ci_corrected[1]],
'p-value': [mean_p_corrected, change_p_corrected, ancova_p_corrected]
})
# 出力の表示を調整して図として表示
fig, ax = plt.subplots(figsize=(10, 3))
ax.axis('off')
ax.axis('tight')
table = ax.table(cellText=results_corrected.values, colLabels=results_corrected.columns, cellLoc='center', loc='center')
table.auto_set_font_size(False)
table.set_fontsize(10)
table.auto_set_column_width(col=list(range(len(results_corrected.columns))))
plt.title("Table 11-3 Effect of Captopril in Antihypertensive Trial Data (Corrected)", pad=20, fontsize=14)
plt.show()
# 表のデータも表示
results_corrected
この結果から、共分散分析が最も狭い信頼区間を出すことがわかりました。
参考文献
『医学のための因果推論Ⅰ 一般化線形モデル』
