
『医学のための因果推論』のための統計学入門:8.分散分析と回帰分析
『医学のための因果推論Ⅰ 一般化線形モデル』を勉強した時のまとめです。
結構難しい本でしたので自分なりの解釈を入れながらまとめました。
統計学の基礎である線形回帰と分散分析(ANOVA)は、データ間の関係性を理解し、仮説を検証するための強力なツールです。
しかし、その背後にある数学的な概念やデザイン行列の直交性といった特性は難解です。
本記事は最小二乗法の原理から始め、直交性が統計モデルに与える影響、正規性、一次従属と多重共線性についてまとめます。
線形回帰と分散分析
分散分析の目的
分散分析(ANOVA)は、複数のグループ間で平均値の差が統計的に有意かどうかを検定する手法です。
データの変動を要因(因子)に分解し、それぞれの要因がどの程度変動に寄与しているかを評価します。
分散分析の基本原理は、アウトカム変数の総平方和(Total Sum of Squares: $${SS_T}$$)を、要因の主効果による平方和(Model Sum of Squares: $${SS_M}$$)と残差平方和(Residual Sum of Squares: $${SS_R}$$)に分解することです。
これは変動の起源を特定し、それぞれの要因がアウトカムの変動をどの程度説明できるかを示します。
数式で表現すると、$${SS_T}$$は次のように定義されます:
$$
SS_T = \sum_{i=1}^{N} (Y_i - \bar{Y})^2
$$
ここで、$${Y_i}$$ は観測値、$${\bar{Y}}$$ は平均値です。
$${SS_T}$$は、$${SS_M}$$と$${SS_R}$$に分解されます。
$$
SS_T = SS_M + SS_R
$$
後述しますが、分散分析は直交設計が成り立つ場合に最も効果的に機能します。
直交設計では各要因の効果が互いに独立に推定できるため、推定結果の解釈もわかりやすくなります。
例えば2因子の分散分析モデルにおいて、Factor1とFactor2が直交している場合、主効果と交互作用は次のようにモデル化されます。
$$
\text{E}(Y) = \beta_0 + \beta_1 X_{Factor1} + \beta_2 X_{Factor2} + \beta_3 X_{Factor1} X_{Factor2}
$$
ここで、$${X_{Factor1}}$$ と $${X_{Factor2}}$$ はそれぞれの因子のダミー変数であり、$${\beta_3}$$ は交互作用効果を示します。
このモデルにおけるパラメータの推定は、最尤法と一致する性質を持つ最小二乗法を用いて行われます。
線形回帰モデルの構造
線形回帰モデルは、目的変数 $${Y}$$ と一つまたは複数の説明変数 $${X_1, X_2, \dots, X_p}$$ との線形関係をモデル化します。
回帰分析の主な目的は、アウトカム(従属変数)と1つまたは複数の共変量(独立変数)との線形関係を推定することです。
一般的な形は以下の通りです。
$$
Y_i = \beta_0 + \beta_1 X_{i1} + \beta_2 X_{i2} + \dots + \beta_p X_{ip} + \varepsilon_i = \beta_0+\sum_{j=1}^p \beta_j X_{i j}+\varepsilon_i
$$
$${\beta_0}$$ は切片(定数項)
$${\beta_j}$$ は説明変数 $${X_j}$$ の回帰係数 (j = 1,…,p)
$${\varepsilon_i}$$は誤差項で、平均0の正規分布に従うと仮定します
このモデルの目的は、データから回帰係数 $${\beta_j}$$ を推定し、説明変数が目的変数に与える影響を明らかにすることです。
モデルの適合度は決定係数($${R^2}$$)によって評価されます。
$${R^2}$$は次のように定義されます。
$$
R^2 = \frac{SS_M}{SS_T}
$$
最小二乗法の原理
残差平方和の最小化
分散分析は複数のグループ間での平均の差異を評価するのに特化しており、要因がカテゴリ変数であり、アウトカムが連続変数である場合に適用されます。
一方回帰分析は、連続的な共変量とアウトカムの関係を定量的に評価する手法です。
これらの手法に共通するのは、尤度原理に基づいてモデルの適合度を評価し、平方和を通じて変動を分解するという点です。
最小二乗法は、観測値とモデルによる予測値の差(残差)の二乗和を最小化することで、最適な回帰係数を求める方法です。
$$
\text{残差平方和 (RSS)} = \sum_{i=1}^n (Y_i - \hat{Y}_i)^2 = (\boldsymbol{Y} - \boldsymbol{X} \boldsymbol{\beta})^\top (\boldsymbol{Y} - \boldsymbol{X} \boldsymbol{\beta})
$$
$${\boldsymbol{Y}}$$ は目的変数のベクトル
$${\boldsymbol{X}}$$ はデザイン行列
$${\boldsymbol{\beta}}$$ は回帰係数のベクトル
最小二乗推定量の導出
残差平方和を最小化する回帰係数の推定値は、以下の正規方程式から得られます。
$$
\hat{\boldsymbol{\beta}} = (\boldsymbol{X}^\top \boldsymbol{X})^{-1} \boldsymbol{X}^\top \boldsymbol{Y}
$$
この解は、デザイン行列 $${\boldsymbol{X}}$$ の列ベクトルが一次独立(後述)である場合に一意に存在します。
一次独立でない場合は逆行列が存在しないため、一般化逆行列を用いた推定が必要です。
平方和の一意性
回帰分析の共変量の単位を変換したり, 分散分析で同じ因子をコーディングだけ変えて指定したりしても平方和の計算結果に差が出ないことを平方和の一意性といいます(回帰係数には違いが生じ得ます)。
デザイン行列と直交性
デザイン行列の役割
デザイン行列はモデルの説明変数を整理した行列で、回帰分析や分散分析で重要な役割を果たします。
各列が説明変数、各行が観測を表し、例えば以下のように表現されます。
$$
\boldsymbol{X} = \begin{pmatrix} 1 & X_{11} & X_{12} \\ 1 & X_{21} & X_{22} \\ \vdots & \vdots & \vdots \\ 1 & X_{n1} & X_{n2} \end{pmatrix}
$$
ここで。1列目は切片項を表します。
直交性の定義
デザイン行列の直交性は、列ベクトル同士の内積がゼロであることを指します。
すなわち、$${\boldsymbol{X}_j^\top \boldsymbol{X}_k = 0 \quad (j \ne k)}$$です。
デザイン行列 $${\boldsymbol{X}}$$ の列が互いに直交している場合、共変量の効果は他の共変量の影響を受けることなく推定することができます。
直交性が成り立つ場合は、次のようにブロック対角行列として表現されます。
$$
\boldsymbol{X}^T \boldsymbol{X} = \left(\begin{array}{ccc} \boldsymbol{X}_1^T \boldsymbol{X}_1 & & \mathbf{0} \\ & \ddots & \\ \mathbf{0} & & \boldsymbol{X}_q^T \boldsymbol{X}_q \end{array}\right)
$$
この場合、回帰係数はそれぞれの共変量ごとに独立に推定されます。
直行性を想定すると、以下のような利点があります。
推定の独立性:各回帰係数の推定が他の説明変数の影響を受けず、解釈が容易になります。
計算の簡略化:直交性により、$${\boldsymbol{X}^\top \boldsymbol{X}}$$ が対角行列となり、逆行列の計算が容易になります。
主効果と交互作用
主効果の概念
主効果は、各因子(説明変数)が単独で目的変数に与える直接的な影響を指します。
例えば因子Aと因子Bがある場合、
$$
Y_i = \mu + \alpha_i + \beta_j + \varepsilon_i
$$
が主効果を表します。
ここで、
$${\mu}$$ は全体平均
$${\alpha_i}$$ は因子Aの主効果
$${\beta_j}$$ は因子Bの主効果
$${ \varepsilon_i}$$は誤差項
です。
交互作用とモデル化
交互作用は、一つの因子の効果が他の因子の水準によって非加法的に変化する現象を指します。
モデルに交互作用項を含めることで、この効果を捉えることができます。
$$
Y_i = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \varepsilon_i
$$
$${(\alpha\beta)_{ij}}$$ は因子Aと因子Bの交互作用効果です。
平方和の分解と分散分析表
分散分析では、全体の変動(総平方和)を要因や誤差に分解します。
$$
\text{総平方和}(SS_T) = \text{要因平方和} (SS_A, SS_B) + \text{交互作用平方和 }(SS_{AB}) + \text{誤差平方和} (SS_E)
$$
平方和の分解は、分散分析や回帰分析でモデルの適合度を評価する際にとくに重要です。
分散分析表
分散分析表は、各要因ごとに分解した要因の平方和、自由度、平均平方、F値などを整理したものです。

正規性の仮定と変数変換
多くの統計手法はデータの分布が正規分布に従う仮定に基づいているため、この正規性が満たされない場合、推定や検定の結果が信頼できなくなる可能性があります。
変数変換による正規性の修正
データの分布を正規分布に近づけるための方法としては以下が一般的です。
対数変換:データが右に歪んでいる場合に有効です。
$$
Y' = \log(Y)
$$
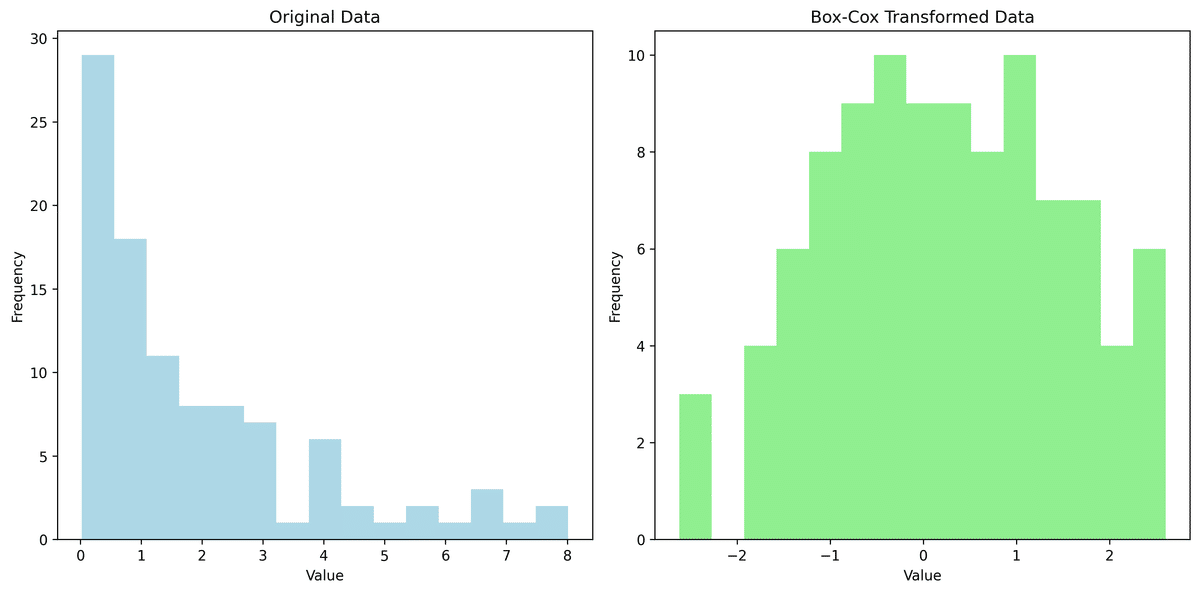
Box-Cox変換:最適な変換パラメータ $${\lambda}$$ をデータから推定します。
$$
Y' = \begin{cases} \dfrac{Y^\lambda - 1}{\lambda} & (\lambda \ne 0) \\ \log(Y) & (\lambda = 0) \end{cases}
$$
from scipy import stats
# ダミーデータの作成:正規分布に従わないデータ
data = np.random.exponential(scale=2, size=100)
# Box-Cox変換
data_transformed, lambda_opt = stats.boxcox(data)
# 結果の表示
print(f'最適なλ: {lambda_opt:.2f}')
# ヒストグラムで変換前後のデータを可視化
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.hist(data, bins=15, color='lightblue')
plt.title('Original Data')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.subplot(1, 2, 2)
plt.hist(data_transformed, bins=15, color='lightgreen')
plt.title('Box-Cox Transformed Data')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.tight_layout()
plt.savefig('boxcox_transform.png', dpi=300, bbox_inches='tight')
plt.close()
Image('boxcox_transform.png')一次従属性と多重共線性
一次従属性
共変量同士の関係が回帰係数の計算へもっとも強く影響するのは, ある共変量が他の共変量の線型結合で表されるときです。
このとき, デザイン行列 $${\boldsymbol{X}}$$ の列ベクトルは一次従属になるため、$${\boldsymbol{X}^T \boldsymbol{X}}$$ の逆行列を計算することができません。
このような場合、なんらかの制約をおいてパラメータの実質的な数を減らす必要があります。
医学研究で一次従属性が生じる状況は2つあり、 一つ目はある共変量が別の共変量から計算されるときです。
典型的なのは身長と体重から求められるBMI, 総コレステロールと HDLコレステロールの差である non-HDLコレステロール, クレアチニンから計算される推定糸球体濾過率 (eGFR) などです。
二つ目の状況はパラメータが冗長なときで、2 群しかないのに3つのパラメータを推定するケースなどが該当します.
多重共線性
多重共線性は、(一次従属ではないが)説明変数間に高い相関がある状態です。
例えば体重の予測式に身長と座高を同時に投入したりしたような場合に発生します。
多重共線性があると、以下のような問題を引き起こします。
回帰係数の推定値が不安定になる。
標準誤差が大きくなり、検定の信頼性が低下する。
分散拡大因子(VIF)
分散拡大因子(VIF)は、多重共線性の程度を測る指標です。
$$
\text{VIF}_j = \dfrac{1}{1 - R_j^2}
$$
$${R_j^2}$$ は、説明変数 $${X_j}$$ を他の説明変数で回帰したときの決定係数です。
一般的にはVIFが1に近いほど多重共線性の問題はほとんどないといえ、VIFが5を超えると多重共線性の可能性が高いといわれています。
VIFが10を超える場合は特に深刻な多重共線性であるといわれますが、あくまで目安の一つであり絶対的なものではありません。
VIFを用いた多重共線性の対処法としては、
高い相関を持つ変数を削除する
主成分分析などの次元削減手法を利用する
などがあります。
具体例:直交した実験計画の設計
性別(男性+1、女性-1)と治療(実薬+1、プラセボ-1)を要因とした実験を考えます。
このとき、デザイン行列が以下のようになったとします。

この場合、直交性を確認すると$${X_1^\top X_2 = 0}$$となりますから、これは直交性があるといえます。

import pandas as pd
import numpy as np
import statsmodels.api as sm
from statsmodels.formula.api import ols
import matplotlib.pyplot as plt
import seaborn as sns
from IPython.display import Image
# ダミーデータの作成:性別(男性/女性)と治療(実薬/プラセボ)の2因子
np.random.seed(0)
data = pd.DataFrame({
'Sex': np.tile(['Male', 'Female'], 20),
'Treatment': np.repeat(['Drug', 'Placebo'], 20),
'Outcome': np.random.normal(10, 2, 40)
})
# 2因子の分散分析のモデルを構築
model = ols('Outcome ~ C(Sex) + C(Treatment) + C(Sex):C(Treatment)', data=data).fit()
anova_table = sm.stats.anova_lm(model, typ=2)
# 分散分析表の表示
print("分散分析表:\n", anova_table)
# 直交性の検証:デザイン行列の作成
# 性別と治療を0/1に変換
data['Sex_code'] = np.where(data['Sex'] == 'Male', 1, 0)
data['Treatment_code'] = np.where(data['Treatment'] == 'Drug', 1, 0)
# 交互作用項の追加
data['Interaction'] = data['Sex_code'] * data['Treatment_code']
# 直交性の確認:相関行列の作成
cor_matrix = data[['Sex_code', 'Treatment_code', 'Interaction']].corr()
# 相関行列の表示
print("\n直交性を確認するための相関行列:\n", cor_matrix)
# 相関行列の可視化
plt.figure(figsize=(8, 6))
sns.heatmap(cor_matrix, annot=True, cmap='coolwarm', vmin=-1, vmax=1, center=0, linewidths=0.5)
plt.title('Correlation Matrix of Factors with Values')
plt.tight_layout()
plt.savefig('design_correlation_with_values.png', dpi=300, bbox_inches='tight')
plt.close()
Image('design_correlation_with_values.png')
# 箱ひげ図で分散分析の結果を可視化
plt.figure(figsize=(8, 6))
data.boxplot(column='Outcome', by=['Sex', 'Treatment'])
plt.title('Boxplot of Outcome by Sex and Treatment')
plt.suptitle('')
plt.xlabel('Group')
plt.ylabel('Outcome')
plt.tight_layout()
plt.savefig('anova_boxplot.png', dpi=300, bbox_inches='tight')
plt.close()
Image('anova_boxplot.png')


from patsy import dmatrix
# 性別と治療の直交デザイン
design_matrix = dmatrix('C(Sex) + C(Treatment) + C(Sex):C(Treatment)', data, return_type='dataframe')
# デザイン行列の表示
print(design_matrix.head())
# 直交性の検証
cor_matrix = design_matrix.corr()
print(cor_matrix)
# 相関行列の可視化
plt.figure(figsize=(8, 6))
plt.imshow(cor_matrix, cmap='coolwarm', interpolation='none')
plt.colorbar(label='Correlation')
plt.title('Correlation Matrix of Design Matrix')
plt.tight_layout()
plt.savefig('design_correlation.png', dpi=300, bbox_inches='tight')
plt.close()
Image('design_correlation.png')
医療研究での分散分析と回帰分析の応用
医療研究では、治療効果や疾患発生率の差異を評価するために分散分析と回帰分析が用いられます。
特にランダム化臨床試験(RCT)においては、直交デザインを適用することで共変量の調整なしに要因の効果を効率的に推定することができます。
観察研究での多重共線性
観察研究では共変量間に強い相関が存在することが多いため、多重共線性の影響を最小限にすることが重要です。
VIFを用いて共変量間の相関を測定し、必要に応じて変数選択や変数変換を行うことが推奨されます。
参考文献
『医学のための因果推論Ⅰ 一般化線形モデル』
