【高校受験　偏差値60を目指す】　関数を絶対に得意にするチャレンジ　part2 先生の出題例

こんにちは。今回は前回のお題作りの次のステップのお話になります。

前のnoteはこちら

テーマとしてカラオケ屋さんの料金の比較をネタに問題を作ろうという試みをしています。

今回は先生が作った問題のサンプルを公開します。

今回はレベルとして
福岡県の公立高校の入試問題レベルを想定しています。

少し福岡の公立高校入試問題についてお話しさせてください。

福岡の公立は大問6つの構成で大問4で関数の問題が出てくることは確定（配点　60点満点中9点）

大問の中の問題は関数では1〜3の3問構成になっています。

それぞれの問題はだいたいコレって決まっています。

ただし、近年この法則が変わっていて、本質がわかってないと戸惑って全滅しかねないほどの難易度に跳ね上がっています。

従来の出題パターン

（1）はただ数字を代入すれば答えられる基本問題

（2）は特定の範囲の直線をyをxの式で表すもの。あるいは適切なグラフを洗濯するもの

（3）で（2）で扱ってない直線の式を求めて、そこからさらに複数のグラフの交点の座標を求める問題。

となっております。

しかし、最近はこんな感じです。

令和3年度の入試問題

令和3年度の問題

変更点まとめ

（1）の時点でyをxの式で表すことが求められる。また、座標の意味することを言葉で説明させる

これはつまるところ、問題の本質、関数の本質を聞いているといっても過言ではありません。

ただ、計算ができるだけでなく、グラフの座標の持っている意味を正しく理解しておく必要があるわけですね。

問題集をがむしゃらに解いているだけではなかなか正答出来ないようになっています。

（2）グラフを描く能力も求められ、より深く関数やグラフの本質の理解を問う問題になっています。
年によってはこの（2）で説明として記述をさせることもあります。

(3)は例年通りのタイプの問題ですが、最近では
この問題を難しくするよりも、この問題にたどり着くまでの難易度をあげて、
相対的に正答率を落としに来ている、という印象です。

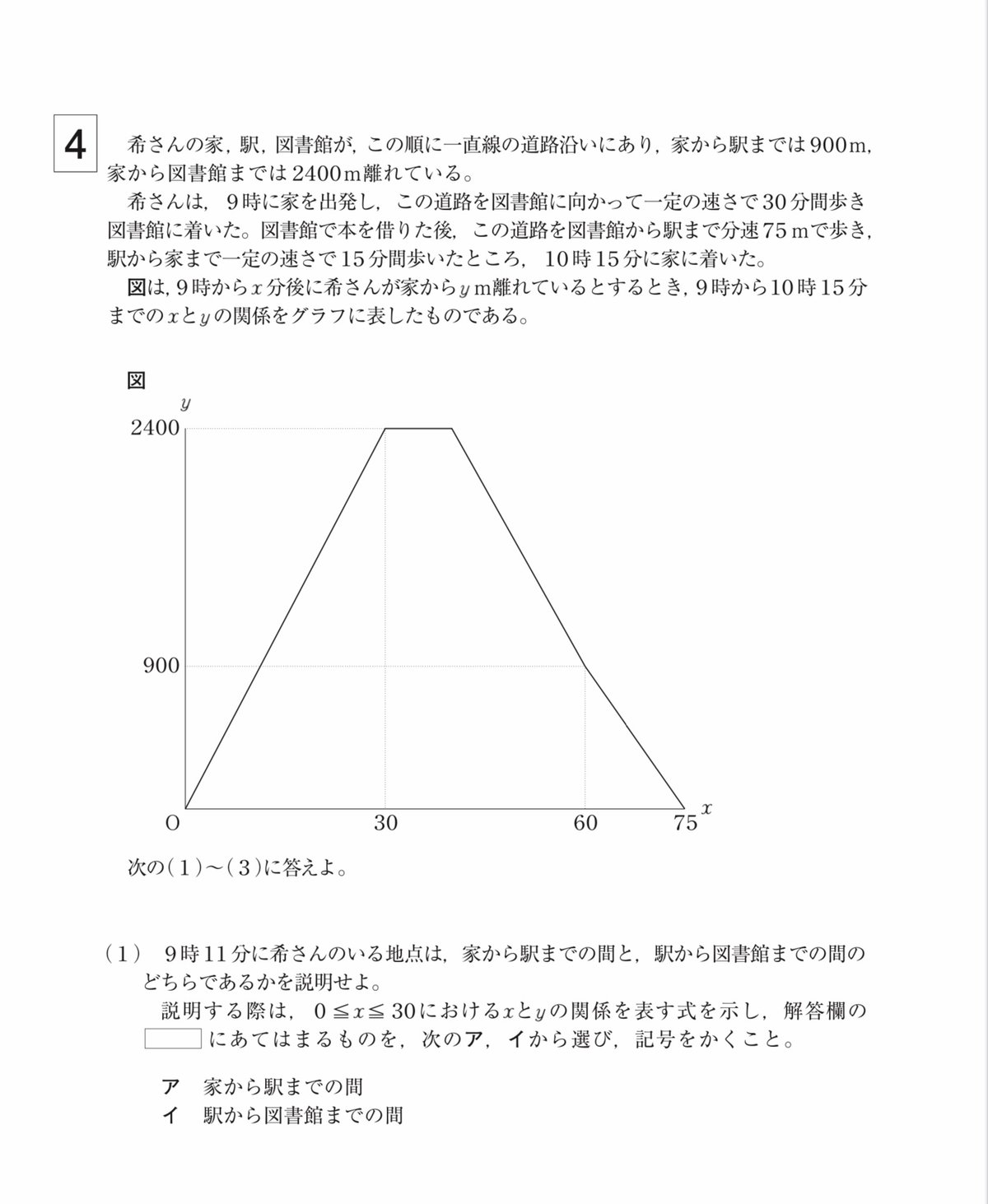
出題例サンプル（難易度　福岡県公立入試レベル）

というわけで今回先生が生徒に練習問題として解かせるために作ったサンプル問題がこちらになります。

実在の店舗名はネットにて公開するものになるため、伏せて作ってます。

(1)＝(3)まですべて過去の福岡県の公立入試問題チックな感じで出しています。

緑の枠の中は他にもこんな感じで問題が出せるよっていう例ですね。

いろいろ出そうと思えばいくらでも問題は作れますが、
作ったあとに自分で模範解答も作らないといけません。

この模範解答を作る段階で、作った問題の欠陥とか不具合が見つかるんですよね。

そこまでを見越して問題を作って出題しますから
生徒が自分で問題を作るというのは非常に効果的です。

ということで今回はここまでになります。

次回は生徒が作ってみた問題を僕の方で少し改定して（問題として成立する形にして）投稿したいと思います٩( 'ω' )و