
描く空間図形
直線と平面の位置関係
初めにちょっと頭の体操。
☆ ℓ , m , n は直線、 α , β , γ は平面である。次の(1)〜(5)から偽のものを選んで、反例を図に描いてみよう。
(1) ℓ ∥m , ℓ ∥n ⇒ m∥n
(2) ℓ ⊥m , ℓ ⊥n ⇒ m⊥n
(3) ℓ ⊥α , ℓ ⊥b ⇒ α∥β
(4) ℓ ⊥α , m⊥α ⇒ ℓ ∥m
(5) α⊥β , α⊥γ ⇒ β∥γ
※ ℓ ⊥m は、ℓ と m が交わっていなくてもかまいません。
平行移動して直角に交わるなら ⊥(垂直)です。
《答え》 偽のものは (2) と (5)
(反例) (2) (5)
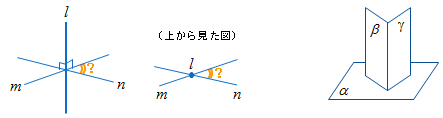
さて、次の課題は、上の(反例)に示した程度のスケッチをすることです。
空間図形を描く(その1)
ここでの目的は、数学の空間図形の問題を考えるために、空間図形を把握することです。ですから、製図の描き方のルールにとらわれず、それっぽく見える図を描ければよいこととします。
ところで、まず確認したいのは空間図形を正確に紙に描くのは無理だということです。それを承知の上で、それっぽくウソを描くしかありません。
さて、まず基本図形の描き方。直線や平面は無限に伸びるものですが、そんなものをそのまま紙に描けるはずがありません。また、球と円を区別して描かなければなりません。というわけで、次のように描きましょう。
直線 平面 球 円

それぞれ「線分、平行四辺形、円、だ円」ではありません。念のため。
それから、見取り図の中に式を立てるのに使える情報も盛り込みたいですね。数学の問題を解くには、そこがポイントです。では、お題です。
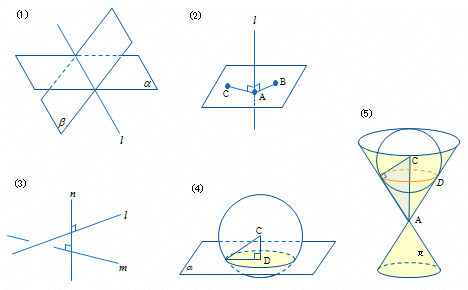
(1) 平行でない2平面 α , β の交線 ℓ
(2) 点 A を通り、平面 ABC に垂直な直線 ℓ
(3) ねじれの位置にある2直線 ℓ , m の両方に直交する直線 n
(4) 球面 C と平面 α の交円 D
(5) 点 A を通り、球面 C に接する直線群(曲面)ならびに接点群(曲線)
見取り図を描くのと合わせて、直角になるところには直角記号を入れておきたいですね。そうすれば「垂直 ⇔ 内積ゼロ」を使って式を立てたり、「三平方定理」 使って長さを求めたりできますから。
空間図形を描く(その2)
続いて、もうちょっと複雑なもの(おもしろいもの)を描いてみましょう。
数学の空間図形の問題でよく出てくるものですが、いきなり計算しようとせず、まず位置関係をつかみましょう。
(1) 2点 A , B が平面αに関して同じ側にあるとき、
「AP+BP が最小となるような平面α上の点 P」
(2) 2点 A , B が直線 ℓ 上になく、A , B と ℓ が同一平面上にもないとき、
「△ABP の面積が最小となるような直線 ℓ 上の点 P」
(3) 直線 m の周りに
(ねじれの位置にある)直線 ℓ を回転してできる回転体
(4) 円すい曲面(2つの円すい)を平面で切ったときの切り口が、
放物線(だ円、双曲線)になる
(5) 光源 A から発した光が、中心が z 軸上にある球に当たって、
その影が xy 平面上の放物線を描く
まずはじめに (4) に関連する(というより、そのまんまですが)話を少々。円すい曲面を平面で切るとき、
母線に平行 もっと寝かせる もっと立てる
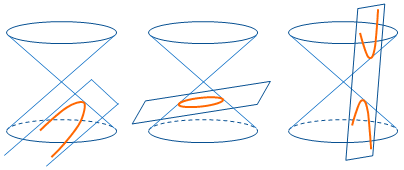
↓ ↓ ↓
放物線 だ円 双曲線
となります。放物線・だ円・双曲線をあわせて2次曲線と呼びますが、「円すいを平面で切ると、切り口は2次曲線になる」ということです。(5) はこのことをふまえて考えてください。
(1) 2点 A , B が平面αに関して同じ側にあるとき、
「AP+BP が最小となるような平面α上の点 P」
→ αに関してAと対称な点を A' とすると、AP+PB= A’P+PB
これが最小になるのは、A’, P , B が一直線上にあるとき。
(2) 2点 A , B が直線 ℓ 上にないとき、
「△ABP の面積が最小となるような直線 ℓ 上の点 P」
→ AB の長さは変わらないから、
三角形の高さが最小になるときを考えればよい。
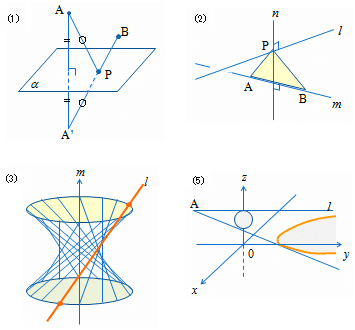
(3) 直線 m の周りに直線 ℓ を回転してできる回転体
→ つづみ形になる。
体積を求めるには、回転軸に沿って積分すればよい。
回転軸を通る平面でこの曲面を切ると、双曲線になる。
(4) 円すい曲面(2つの円すい)を平面で切ったときの
切り口が、放物線(だ円、双曲線)になる
→ 母線に平行な平面で切ると、放物線。
もっと寝かせると、だ円。
もっと立てると、双曲線。
(5) 光源 A から発した光が、中心が z 軸上にある球に
当たって、その影が xy 平面上の放物線を描く
→ 円すい(球の影)を平面(xy 平面)で切るのと同じこと。
切り口が放物線だということは、直線ℓと xy 平面は平行。
楽しんでお絵描きしてくださいませ。
◇ ◇ ◇
〜 立体図形の描き方 〜
▷ 見取り図3種
▷ 正多面体つながり
▷ 描く空間図形
▷ 立方体と正四面体の展開図
▷ 円柱どうし、角柱どうしの交わり
