（続）コラッツ予想解明への新解析手法の紹介７ー問題の意味が小学生でもわかる高額懸賞金数学歴史的未解決問題
「コラッツ予想解明への新解析手法の紹介」は「第１章 新手法の紹介の前に」からご覧ください。
新手法要約動画 ←クリック
「（続）コラッツ予想解明への新解析手法の紹介」では第Ｃ１章からご覧ください。
第Ｃ１章には（続）新解析手法の各Ｃ・章へのリンクが貼ってあります。
第Ｃ５章 ＣＳ直線式の美しい法則と公式
第Ｃ１章と第Ｃ２章はコラッツ予想の論法の是非に活用できる内容、第Ｃ３章は新手法を使ったコラッツ予想の解明のヒントとなる内容です。第Ｃ４章で連続関数に触れましたので、ＣＳ直線式の美しい法則と公式について触れておきます。
ＣＳ直線式：
$$
\begin{array}{}
&(c4.1)& & f_{c}(x)=\cfrac{3}{2}x+\cfrac{1}{2}& &(0\le x <1/3)& \\\
\\\
&(c4.2)& & f_{s}(x)=\cfrac{3}{4}x-\cfrac{1}{4}& &(1/3 \le x <1)
\end{array}
$$
（$${x \ge 0}$$ としていますが、ＣＳ直線式では$${(0, 1/2)}$$は含みません。$${(c(1), c(1))}$$は原点で、解析には$${x=0}$$も含みますので、それにあわせて、$${x \ge 0}$$としたまでです。）
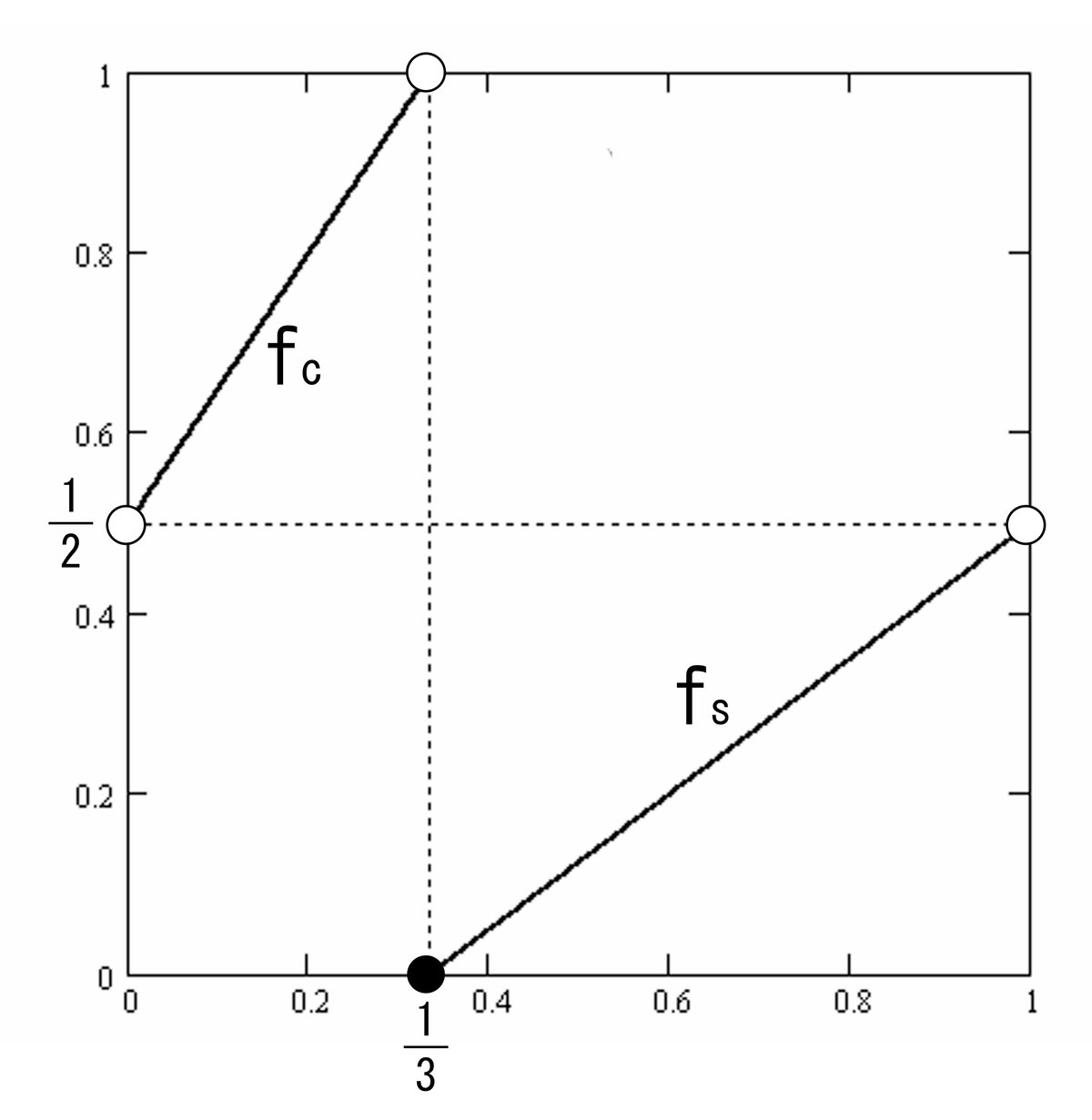
ＣＳ直線式には交換則が成立します。
$${(6.1) \bf f_{c}(f_{s}(x))=f_{s}(f_{c}(x))}$$（$${x}$$は実数）
$$
\begin{array}{}
& f_{c}(f_{s}(x))=\cfrac{3}{2} \Big (\cfrac{3}{4}x-\cfrac{1}{4}\Big)+\cfrac{1}{2}=\cfrac{9}{8}x+\cfrac{1}{8}& \\\
\\\
& f_{s}(f_{c}(x))=\cfrac{3}{4}\Big (\cfrac{3}{2}x+\cfrac{1}{2}\Big)-\cfrac{1}{4}=\cfrac{9}{8}x+\cfrac{1}{8}&
\end{array}
$$
交換則を使えば、$${f_{c}}$$を$${p}$$回、$${f_{s}}$$を$${q}$$回行った後の以下の公式を導くことができます。$${n=p+q}$$
$${(6.2) \bf F_{n}(x)= \Big(\cfrac{3}{2}\Big)^p\Big(\cfrac{3}{4}\Big)^q (x+1)-1}$$
$${f_{c}(x), f_{s}(x), F_{n}(x)}$$は全て$${(-1, -1)}$$を通ります。
式には分数は$${3/2}$$ と$${3/4}$$のべき乗しかなく、 $${p, q}$$が何回であろうと、どの直線も全て$${\bf (-1, -1)}$$を通る、とは美しいですね。
数学的帰納法で(6.2)を証明しておきます。
$${n=1}$$のとき$${(p,q)=(1,0)}$$もしくは$${(p,q)=(0,1)}$$を(6.2)に代入すれば、明らかに成立。
$${F_{n+1}(x)=\cfrac{3}{2}F_{n}(x)+\cfrac{1}{2}=\cfrac{3}{2} \Bigg( \Big(\cfrac{3}{2}\Big)^p\Big(\cfrac{3}{4}\Big)^q x+\Big(\cfrac{3}{2}\Big)^p\Big(\cfrac{3}{4}\Big)^q-1\Bigg)+\cfrac{1}{2}}$$
$${= \Big(\cfrac{3}{2}\Big)^{p+1}\Big(\cfrac{3}{4}\Big)^q x+\Big(\cfrac{3}{2}\Big)^{p+1}\Big(\cfrac{3}{4}\Big)^q-1}$$
$${F_{n+1}(x)=\cfrac{3}{4}F_{n}(x)-\cfrac{1}{4}=\cfrac{3}{4} \Bigg( \Big(\cfrac{3}{2}\Big)^p\Big(\cfrac{3}{4}\Big)^q x+\Big(\cfrac{3}{2}\Big)^p\Big(\cfrac{3}{4}\Big)^q-1\Bigg)-\cfrac{1}{4}}$$
$${= \Big(\cfrac{3}{2}\Big)^{p}\Big(\cfrac{3}{4}\Big)^{q+1} x+\Big(\cfrac{3}{2}\Big)^{p}\Big(\cfrac{3}{4}\Big)^{q+1}-1}$$
よって$${n+1}$$でも成立。
尚、ＣＳ直線式のグラフから以下は自明です。
$${\bf f_c}$$は２回以上は連続して続かない、$${\bf f_s}$$は３回以上は連続して続かない、です。
(6.2)式は最初は交換則を適用して、地道にゴリゴリ計算して導いたわけですが、導いてしまえば数学的帰納法を使えば簡単に証明できてしまいます。便利な証明法ですね。ほか、こんな式になるだろうと予想できれば、あとは数学的帰納法を使って証明する、もいいですね。
この公式も使って、今後諸解法を検討していくことも考えています。
新手法第１章から第８章および（続）新手法第Ｃ５章
までの変数・定義語・関数
$${N}$$、$${No}$$、総ステップ数、ステップ番号、
ＣＳ振動、Ｃ変換、ＣＳプロット、ＣＳ直線式、３Ｃ＋１変換、
３Ｓ＋１変換、Ｓ変換、（一般）コラッツ空間、ＣＳ空間、ｔツリー、
ローレンツプロット、周期軌道、周期点、不動点、究極的な周期点、クモの巣図法、ＣＳ交互変換プロット、不動点$${\left(\cfrac{1}{3},0\right)}$$、
ＣＳ写像、最終点、最終到達点、３Ｃー１変換、３Ｓー１変換、
Ｃグループ、Sグループ、ａ点、ｂ点、ｃ点、ｄ点、
シャルコフスキーの定理、シャルコフスキー順序
距離$${D}$$、$${c(N)}$$、
$${6t+5}$$型、$${6t+1}$$型、$${4t+3}$$型、$${8t+1}$$型、など
$${z_{s}}$$、$${f_{c}(x)}$$、$${f_{s}(x)}$$、$${Nc}$$、$${Ns}$$、$${Nv}$$、$${Nw}$$、$${m_{o}}$$、$${m_{c}}$$、$${m_{s}}$$、$${t_{c}}$$、$${t_{s}}$$、$${t}$$、$${Mo}$$、$${cs(mo)}$$、$${s(Mo)}$$、$${f}$$、$${g}$$
$${\epsilon_b}$$、$${\epsilon_c}$$、$${b_{\epsilon}}$$点、$${ c_{\epsilon}}$$点、
$${u_{cs}(x)}$$、$${u_{c}(x) (x<1/3)}$$、$${u_{s}(x) (x\ge 1/3)}$$、
$${d_{cs}(x)}$$、$${d_{c}(x) (x<1/3)}$$、$${d_{s}(x) (x\ge 1/3)}$$、
$${\bf F_{n}(x)}$$