
(続)コラッツ予想解明への新解析手法の紹介5ー問題の意味が小学生でもわかる高額懸賞金数学歴史的未解決問題
「コラッツ予想解明への新解析手法の紹介」は「第1章 新手法の紹介の前に」からご覧ください。
新手法要約動画 ←クリック
「(続)コラッツ予想解明への新解析手法の紹介」では第C1章からご覧ください。
第C1章には(続)新解析手法の各C・章へのリンクが貼ってあります。
第C4章 コラッツ予想のループについての考察
C4.1 用語の説明
最初に具体例で説明した方が、内容が把握しやすいので、初期値27(3S+1変換)を例にとって説明します。
図C4-1(左)は初期値27(3S+1変換)のCSプロットグラフで、CS直線$${f_c, f_s}$$および補助線$${x=1/3, y=1/2}$$も示してあります。 CSプロット点は全部で41個あります。
図C4-1(右)はCSプロット点のみを表示してあります。
$${f_c}$$より上に、近くに16個のプロット点があり、これをCグループと呼ぶことにします。また端のプロット点をそれぞれa点、b点と呼びます。 $${f_s}$$より上に、近くに24個のプロット点があり、これをSグループと呼ぶことにします。また端のプロット点をそれぞれc点、d点と呼びます。 x軸上に最終点$${(c(5), c(1))}$$が1個あります。
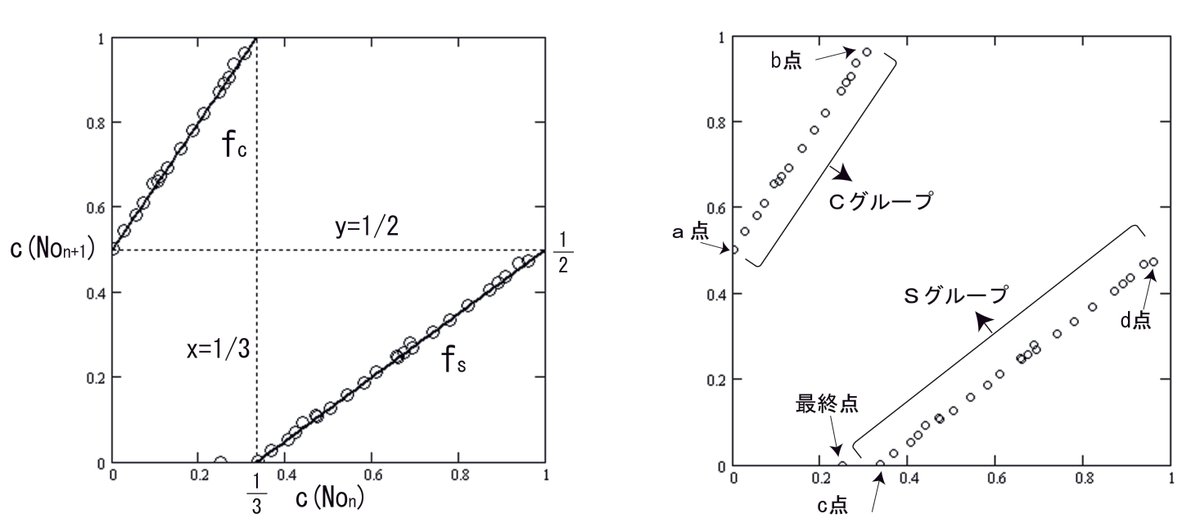
(右)用語の説明図
Cグループ、Sグループ、a点、b点、c点、d点は、初期値27に限らず一般化した場合にも用いることにします。
1以外のループの存在の有無を検討する場合、x軸上にある最終点は考慮する必要ありません。最終点も含んでいるのであれば1に到達する初期値となるからです。
従って1以外のループの存在の有無を検討する場合はCグループとSグループのCSプロット点のみ考慮すればOKです。
C4.2 連続関数の定義
なぜ連続関数(連続写像)を考えるかですが、カオス力学な定理(記事6)を適用したいからです。
図C4-2のグラフはCグループの全てのプロット点を直線で結び、Sグループの全てのプロット点を直線で結んだグラフです。最終点(x軸上)は除いてあります。
直線で結べばそのグラフは必ずCS直線より上にきますから直線で結ぶとしたわけですが、必ずCS直線より上にくる(ベスト)フィット関数でもよいです。

連続させるにはb点とc点を結びたいわけですが、一般化した場合(可算無限個:後述)にも適用できるように図C4-3のようにつなげます。

左図においてb点と$${(1/3, 1)}$$を直線で結びます。$${(1/3, 1)}$$からxの負の方向に正実数$${(\bf \epsilon_b>0)}$$だけ、$${b_x<1/3-\epsilon_b}$$となるようにとり、そこからy方向に直線を伸ばします。これと、b点と$${(1/3, 1)}$$を結んだ直線との交点を$${\bf b_{\epsilon}}$$点と呼ぶことにします。
同様に右図においてc点と$${(1/3, 0)}$$を直線で結びます。$${(1/3, 0)}$$からxの正の方向に正実数$${(\bf \epsilon_c>0)}$$だけ、$${1/3+\epsilon_c < c_x}$$となるようにとり、そこからy方向に直線を伸ばします。これと、c点と$${(1/3, 0)}$$を結んだ直線との交点を$${\bf c_{\epsilon}}$$点と呼ぶことにします。
b点と$${b_{\epsilon}}$$点、$${b_{\epsilon}}$$点と$${c_{\epsilon}}$$点、$${c_{\epsilon}}$$点とc点を結べば、全てのCSプロット点を通る連続な関数(連続写像)を得ることができます。
この全てのCSプロット点を通る連続な関数(連続写像)を
$${\bf u_{cs}(x)}$$、また$${\bf u_{c}(x) (x<1/3)}$$、$${\bf u_{s}(x) (x \ge 1/3)}$$
と呼ぶことにします。
全く同様にして3S-1変換でも、全てのCSプロット点を通る連続な関数を
$${\bf d_{cs}(x)}$$、また$${\bf d_{c}(x) (x<1/3)}$$、$${\bf d_{s}(x) (x \ge 1/3)}$$
と呼ぶことにします。
$${1/3}$$の等号はどちらに入れてもいいのですがCS直線の場合と同じにしました。
連続関数が定義されても、ループの存在の有無はあくまでも連続関数上のCSプロット点上での有無です。CSプロット点以外の実数の点でループが見つかったとしてもループが存在するとは言えません。
可算無限個のCSプロット点は表示できませんので初期値27(3S+1変換)と初期値153(3S-1変換)のグラフで上記諸関数を図C4-4に示しました。
$${\bf u_{c}(x)}$$、$${\bf u_{s}(x)}$$の示す範囲を$${\bf u_{cs}(x)}$$と共に左図に、また、$${\bf d_{c}(x)}$$、$${\bf d_{s}(x)}$$の示す範囲を$${\bf d_{cs}(x)}$$と共に右図に示しました。縦点線は$${x=1/3}$$です。
$${b_{\epsilon}}$$のx座標<$${c_{\epsilon}}$$のx座標ですので、2点を結ぶ直線の傾きは負です。またこの部分で$${x=1/3}$$と交わります。
$${\bf u_{cs}(x)}$$、$${\bf d_{cs}(x)}$$はxの一価連続関数となります。

(右)dcsのグラフとdc、dsの範囲
C4.3 可算無限個のCSプロット点と連続関数について
全ての初期値(無限個の正奇数$${No}$$)のCSプロット点を表示させた場合を考えます。
初期値が最終的に1に到達する、無限ステップ数となる、ループする(1以外)、のどれであっても関係ありません。CSプロット点は全て合わせれば
$${f_c}$$より上に、近くに可算無限個のプロット点が、
$${f_s}$$より上に、近くに可算無限個のプロット点が、
x軸上に可算無限個のプロット点(最終点)が、
現れます。
”近くに”とは、$${2^{68}}$$以上の奇数ではCS直線との差は高々$${10^{-21}}$$程度です(セクションC3.1、証明はC3.4)。
3種の可算無限個のプロット点は、全ての正奇数$${No}$$において
3S+1変換では、新手法第3章、3.1式
$${3No+1=m_{o} \cdot 2^n }$$ の $${(c(No), c(m_{o}))}$$ のことです。
3Sー1変換では、新手法第C2章、C2.1式
$${3No-1=m_{o} \cdot 2^n }$$ の $${(c(No), c(m_{o}))}$$ のことです。
ここで$${m_{o}}$$は正奇数、$${n}$$は正整数。
1以外のループの存在の有無を検討する場合、x軸上にある可算無限個のプロット点(最終点)は考慮する必要ありません。最終点を含むことは1に到達することだからです。
x軸上にある可算無限個のプロット点(最終点)のx座標は、
3S+1変換では、新手法第3章3.2の(3.13)式で$${t_s=0}$$と置いた奇数値のC値の集合、$${{c(1),\ c(5), \ c(21), \ c(85), \cdots}}$$のことです。
極限値は$${\cfrac{1}{3}}$$です。
$${(3.13) (再)cs(6t_s+1)={8t_s+1,\ 32t_s+5, \ 128t_s+21, \ 512t_s+85, \cdots}}$$
3Sー1変換では、第C2章の(c2.19)式で$${t_w=0}$$と置いた奇数値のC値の集合、$${{c(1),\ c(3), \ c(11), \ c(43), \cdots}}$$のことです。
極限値は$${\cfrac{1}{3}}$$です。
$${(c2.19) (再)cs(6t_w+1)=\{4t_w+1,\ 16t_w+3, \ 64t_w+11, \ 256t_w+43, \cdots\}}$$
可算無限とは可付番無限とも呼ばれ、高校数学の範囲を超えますが、無限の濃度にも濃さがあり、最小の濃度で、自然数全体の集合と1対1の対応が付く濃度です。
例えば、正奇数、$${1, 3, 5, 2n-1, \cdots}$$は自然数$${n}$$と1対1の対応が付くので可算無限集合の1つです。無限の世界では奇数と自然数の濃度が同じである、というのですから摩訶不思議です。尚、実数の集合は自然数と1対1の対応が付かないで、非可算無限といいます。
無限の不思議さですがリーマン予想に出てくるゼータ関数の自然数の和、$${1+2+3+\cdots =-\cfrac{1}{12}}$$ となります(オイラー、1749年)。
分数になるのも不思議ですが、さらにマイナスとは・・。
有理数は可算無限集合です。
C値は有限小数、有理数の1つなので、全ての正奇数$${\bf No}$$のC値の集合は可算無限集合です。
a点と$${(0, 1/2)}$$およびd点と$${(1/2,1)}$$については上記と同様の手順は必要ありません。a点、d点は全てのCSプロット点を通る連続関数の$${(0, 1/2)}$$および$${(1/2,1)}$$に限りなく近づく端の点です。($${\cfrac{1}{2^n}}$$の集合において、$${n}$$無限大としたときの$${\cfrac{1}{2^n}}$$と$${0}$$の関係に同じです。また、どんなに大きい$${n}$$をとって、$${\cfrac{1}{2^n}}$$を$${0}$$に近づけても、それより更に$${0}$$に近い実数が存在します。)
尚、Cグループに属するC値は0より大きく、Sグループに属するC値は1より小さい、またC値$${\ne 1/3}$$です。
可算無限個の要素を持つCグループの端のb点は限りなく$${(1/3,1)}$$に
近い点が存在しますが、それに応じて、$${\epsilon_b>0}$$をとって$${b_{\epsilon}}$$点を定めることができます。
Sグループの端のc点についても同様で、$${c_{\epsilon}}$$点を定めることができます。
命題A:
3S+1変換における可算無限個のCSプロット点を通る1価連続関数$${\bf u_{cs}(x)}$$を定めることができ、
3S-1変換における可算無限個のCSプロット点を通る1価連続関数$${\bf d_{cs}(x)}$$を定めることができる。
命題Aは正であるとして、説明を進めていきます。
新手法第1章から第8章および(続)新手法第C4章(前半)
までの変数・定義語・関数
$${N}$$、$${No}$$、総ステップ数、ステップ番号、
CS振動、C変換、CSプロット、CS直線式、3C+1変換、
3S+1変換、S変換、(一般)コラッツ空間、CS空間、tツリー、
ローレンツプロット、周期軌道、周期点、不動点、究極的な周期点、クモの巣図法、CS交互変換プロット、不動点$${\left(\cfrac{1}{3},0\right)}$$、
CS写像、最終点、最終到達点、3Cー1変換、3Sー1変換、
Cグループ、Sグループ、a点、b点、c点、d点、可算無限個、
1価連続関数(写像)、
距離$${D}$$、$${c(N)}$$、
$${6t+5}$$型、$${6t+1}$$型、$${4t+3}$$型、$${8t+1}$$型、など
$${z_{s}}$$、$${f_{c}(x)}$$、$${f_{s}(x)}$$、$${Nc}$$、$${Ns}$$、$${Nv}$$、$${Nw}$$、$${m_{o}}$$、$${m_{c}}$$、$${m_{s}}$$、$${t_{c}}$$、$${t_{s}}$$、$${t}$$、$${Mo}$$、$${cs(mo)}$$、$${s(Mo)}$$、$${f}$$、$${g}$$
$${\bf \epsilon_b>0}$$、$${\bf \epsilon_c>0}$$、$${\bf b_{\epsilon}}$$点、$${\bf c_{\epsilon}}$$点、
$${\bf u_{cs}(x)}$$、$${\bf u_{c}(x) (x<1/3)}$$、$${\bf u_{s}(x) (x\ge 1/3)}$$、
$${\bf d_{cs}(x)}$$、$${\bf d_{c}(x) (x<1/3)}$$、$${\bf d_{s}(x) (x\ge 1/3)}$$
この記事が気に入ったらサポートをしてみませんか?
