
コラッツ予想解明への新解析手法の紹介2ー 問題の意味が小学生でもわかる数学の高額懸賞金歴史的未解決問題 ー

第2章 CS振動の導出とCSプロット
第2章(2回目)をご覧になる前に「第1章 新手法の紹介の前に」をご覧ください。特にCS振動については「第1章、1.9 新手法の説明の前に」で紹介されていますが、2.1に再度掲載(一部変更および追加)します。
また第1章には各章へのリンクが貼ってあります。
「(続)コラッツ予想解明への新解析手法の紹介」では第C1章からご覧ください。
第C1章には(続)新解析手法の各C・章へのリンクが貼ってあります。
2.1 CS振動とは
コラッツ予想のルール「奇数なら3倍して1を足す、偶数なら2で割る」におきまして、偶数は2で割っていくと必ず奇数に到達しますので、奇数のみを追っていき、偶数は特に断らない限り表記しないこととします。例えば 13の例では、$${13 \to 5 \to 1}$$のように奇数のみ表記します。1に到達するまでの総ステップ数は$${\to}$$の総数で13の場合は総ステップ数=2と数えます。
$${No}$$を正奇数としまして、$${No=27}$$は数は小さいのに以下のように総ステップ数は41もあります。奇数のみ追っていて、最大数は3077です。

この奇数変化を横軸にステップ番号(27は番号0、1は番号41)
を、縦軸に各番号の奇数の値を表示したのが図2-2です。
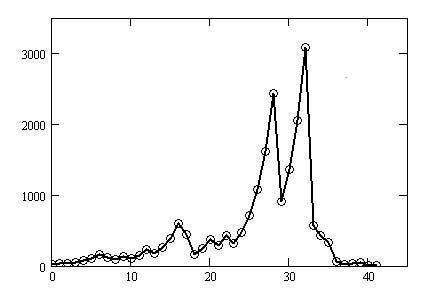
図2-2のグラフに新手法で変換を施すと図2-3となります。
CS振動 と呼ぶことにします。CはコラッツのCも兼ねています。
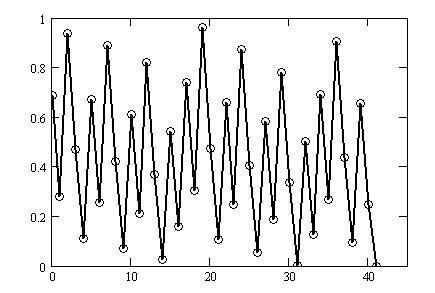
図2-3は図2-2に比べて規則性や周期性が見て取れます。この規則性はまだ序の口でして、さらに幾つか変換を施していきます。するとより一層明確な規則性が見えてきます。初期値が27以外でも総ステップ数の違いこそあれ同様の傾向が現れます。最終的には任意の正奇数$${No}$$について、この傾向を説明する一般式と命題を紹介します。第2章2.2から順を追って解説していきます。
2.2は第2章の有料記事となりますが、CS振動図(図2-3)を見てご判断していただきたくお願い申し上げます。
また第4章4.1(前章までの概要および)図4-1も及びそれ以降の章の内容も大変参考になります。
第2章2.2の内容としましては、図2-3は$${No=27}$$についてのCS振動グラフですが、一般の正奇数$${No}$$についてのCS振動グラフを導く式を紹介します。さらにこの式からCS振動に現れる点をもとにした座標点が2種に分類でき、その特性を$${No=27}$$を例にとり説明します。2種を表す直線式の一般証明はキーとなる証明で同章別セクション2.3、別記事とさせていただきました。
この2種直線式も大変重要でして、上記座標点はこのままでは”近似的に”2種式で表せますが、ある変換を施すことにより、任意の正奇数$${No}$$の初期値に対して途中ステップの正奇数も全てこの直線上の点に”完全に”乗せることができます。つまり2種直線式上に全てのステップの正奇数$${\bm{No}}$$が乗ってしまうということです(第4章図4-1参照)。この説明に背景を含め3章以降章をさくことになります。
コラッツ予想解明のヒントにしたい、さらに深いところまで知りたい場合はこの章、セクション以降もぜひご覧ください。
証明は中高数学でできるだけわかりやすくを心掛けております。記事内容や証明で「なるほど」とお感じになったら、評価の程よろしくお願いいたします。今後の解析の奮起につながります。
第2章2.2までの変数・定義語・関数
$${N}$$、$${No}$$、
総ステップ数、ステップ番号、CS振動、C変換、CSプロット、
CS直線式、
$${c(N_o)}$$、$${z_{s}}$$、$${f_{c}(x)}$$、$${f_{s}(x)}$$
2.2 CS振動の導出式とCSプロット
ここから先は
¥ 800
Amazonギフトカード5,000円分が当たる
この記事が気に入ったらチップで応援してみませんか?
