画像フィルタについてメモ
随時更新
2023/11/30 Canny Edge Detectorまで執筆
2023/12/01 エッジ保存スムージングの追加、先鋭化の追加
画像フィルタ
画像処理分野において、画像に対して何かしらの処理、雑音を除去したり、ある特徴を抽出したり、検出したりなどを行うある処理の事を画像フィルタという。
大きく、空間フィルタと周波数フィルタの2種類が存在する。
これらは、空間領域に対して処理するか、周波数領域に対して処理するかというフーリエ変換・逆フーリエ変換でどちらの領域に対して処理するかということで本質的には同じことをしているフィルタも存在する。処理しやすい方に対して基本的には行う。
空間フィルタリング
Spatial Filtering
入力画像の対応する画素値だけでなく、その周囲の画素も含めた領域内の画素値を用いて出力画像の対応する画素値を計算する方法。「線形フィルタ(LinearFilter)」と「非線形フィルタ(Nonlinear Filter)」に分けられます。線形フィルタとは、入力画像をf (i, j)、出力画像をg (i, j) とすると、以下の式で表現できるものです。
一般に線形フィルタは、入力画像を$${f(i, j)}$$としたとき、出力画像を$${g(i,j)}$$とするとき、以下のように計算される。
$$
g(i, j) = \Sigma^{W}_{n=-W} \Sigma^{W}_{m = -W} f(i+m, j+n) h(m,n)
$$
$${h(m,n)}$$はフィルタの係数を表す配列(重み係数行列)であり、フィルタの大きさは $${(2W+1)* (2W + 1)}$$である。
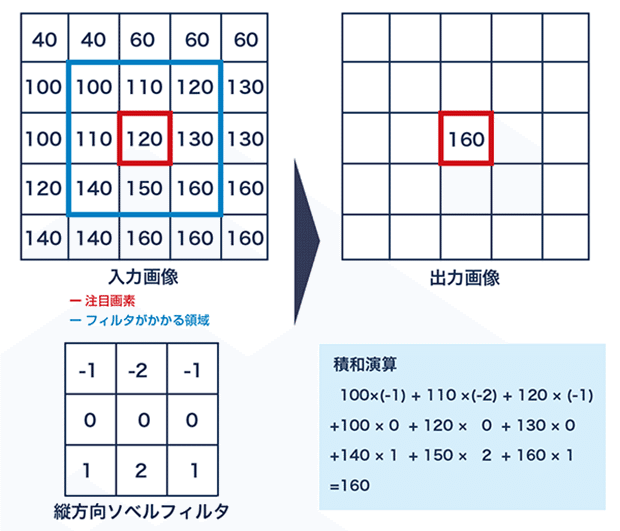
下の例ではフィルタが3x3のフィルタになっているとして、出力画像の$${(i, j)}$$番目の出力を考えているとします。それに対応する入力画像の$${(i,j)}$$の画素を中心にフィルタの原点を合わせます。この場合の入力画像の$${(i, j)}$$番目を注画素と呼びます。下の例では120となっている赤の囲まれた画素です。このとき、重なった位置同士でフィルタの係数と入力画素の値を掛け算し、それをすべて足し合わせる、積和演算を行います。それで出てきた値が出力画像の画素値とします。
ただし、場合によっては結果の値が8bitの0-255の値を想定していたとして、祖rを超えてしまうことがあると思います。その場合はその範囲に収まるように何かしらの手法で正規化を行ったり、収めたりしなくてはいけません。
どんどんと$${(i,j)}$$の位置を順にずらしながら、画像全体にわたって行います。
一般にこの演算は畳み込み演算と呼ばれるような処理になる。
このフィルタリング処理を画像全体に対して行うのではなく、Photoshopなどを想像してもらって、そのブラシの一部の領域にのみ処理するということも考えられます。
フィルタをカーネルと呼ぶ場合もある。機械学習でも畳み込み演算(Convolution)をよく行うため、このフィルタ処理みたいなものがよく起きていると思ってもさほど間違っていない。
一方として、この手順に当てはまらないようなフィルタ処理に関しては、すべて非線形フィルタとなる。
平滑化
ブラーのかかった、ボケた画像や濃淡変化低いような画像を画像処理によって与えるためには、平滑化(smoothing)と呼ばれるフィルタを考えます。画像に含まれるノイズなどの不要な濃淡変動を軽減するためにも使われたりします。
下記の様々な平均化のフィルタ手法を何度か適用させて、回数を重ねることで効果を強めることもできる。
平均化フィルタ
averaging filter
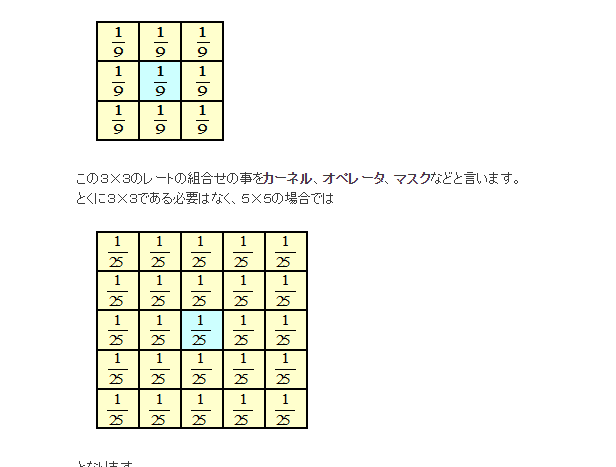
フィルタによっておおわれる領域の画素値の平均値を求めて出力画像にするような3x3フィルタよりも、5x5画素の平均化フィルタのでは平滑化の効果がより強くなっていることが分かる。
フィルタを移動させながら次々に局所的な平均値を求めるため、移動平均フィルタと呼ぶこともある。
box blurと呼んでいるソフトウェアも存在する。下記の重み付き平均と比べて、n x nのフィルタ全体からの影響でblurをかけているため、見た目的な形からboxという名前になっている。


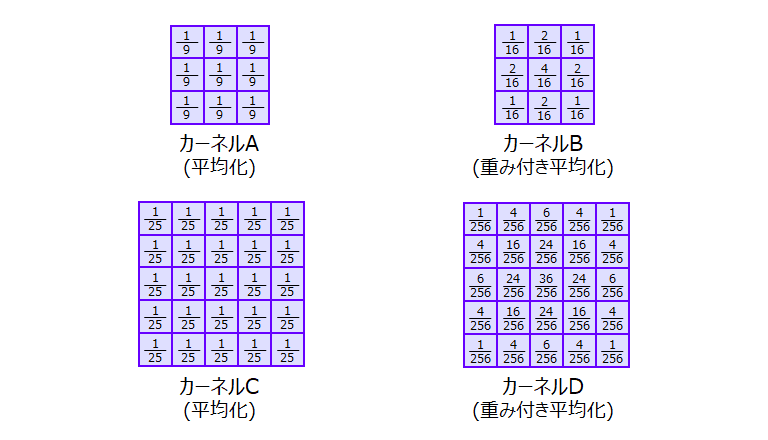
重み付き平均化
単純な平均足立ではなく、フィルタの原点に近いほど大きな重みをつけるなど、重みをつけるパターンの平均フィルタ。
フィルタの重みに関しては合計1になるようにするのが、定番。1にすること見た目の明るさをあまり変わらないようにするため。
加重平均化フィルタ
weighted averaging filter
フィルタの原点に近いほど大きな重みをつける

ガウシアンフィルター
Gaussian filter
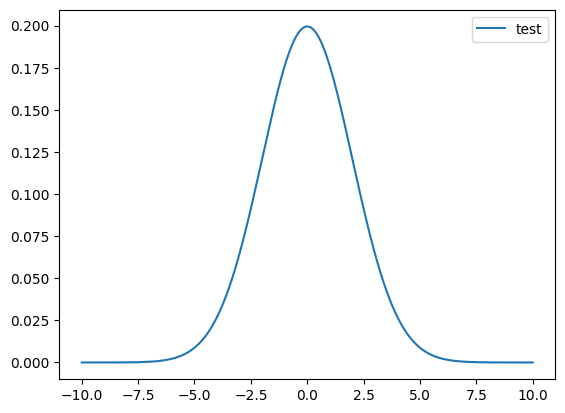
重みをガウス分布(Gaussian Distribution)に近づけたものをガウシアンフィルタと呼ぶ。ガウスぼかしのよう名前でもよく呼ばれる。
平均0, 分散$${\sigma}$$のガウス分布は以下で表される。
$$
h_g(x) = \frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{x^2}{2\sigma^2})
$$
2次元に拡張した2次元ガウス分布はいかになる。
$$
h_g(x,y) = \frac{1}{2\pi\sigma^2}\exp(-\frac{x^2+y^2}{2\sigma^2})
$$
実装としては、5x5のガウスフィルターを適用させると、1画素に対して、25画素分の計算が必要になるため、重めの作業になる。そのため、縦方向と横方向のx,yのそれぞれのガウスに分けてそれぞれ適用させることが数学的にも同等になるため、そうすると、10回ほどの処理で済むこととなる。
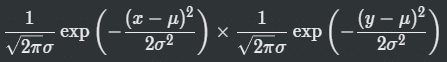
つまり、ガウス関数を用いると、小さくぼかすための係数も、大きくぼかすための係数も、パラメータ一つで簡単に算出することが可能になります。また、先ほどのグラフは二次元のグラフでしたが、ガウス関数は三次元で計算した場合でも、釣り鐘の頂点部分からどの程度の距離にあるのかによって、円形に正しく係数を算出することができます。
さらに、ガウス関数を三次元で用いる場合には x 方向と y 方向を切り離して処理することができます。実はこれが非常に重要です。
たとえば、以前のテキストで解説したときに用いた 5 x 5 のカーネルでは、一つのフラグメントを処理するために 25 パス必要でしたよね。
これは単純に 5 x 5 = 25 という処理回数が必要になるからです。しかし、ガウス関数を用いると x と y を切り離して別々に処理することができるため、5 + 5 = 10 という具合に、パスを大幅に削減できます。これが、gaussian フィルタが高速に動作するということの答えです。
ぼかす範囲が大きくなればなるほど、この恩恵は大きくなります。10 x 10 の範囲を参照するぼかし処理を実装しようと思ったら、普通にぼかし処理を行なうには一つのフラグメントあたり 100 パスもの処理が必要になりますが、gaussian フィルタならたったの 20 パスで済みます。これはとてつもなく大きな処理軽減に繋がりますね。
平均化フィルタに比べて、より滑らかで自然な結果が期待できる。
TouchDesignerで、GLSLで実装した場合の5x5のガウシアンフィルタの例
sigmaに関してはuniform変数にしている。
#define M_PI 3.1415926535897932384626433832795
uniform vec2 sigma;
out vec4 fragColor;
float gauss(float x, float y, float sigma){
float exponent = - (x * x + y * y) / (2 * sigma * sigma);
float denominator = 2 * M_PI * sigma * sigma;
return exp(exponent) / denominator;
}
void main()
{
float weight = 0.0f;
vec4 fc = vec4(0);
//textureOffset()でivec2でオフセットした位置のpixelの値をゲットできる。
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-2, -2)) * gauss(-2, -2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-1, -2)) * gauss(-1, -2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -2)) * gauss(0, -2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 1, -2)) * gauss(1, -2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 2, -2)) * gauss(2, -2, sigma.x);
weight += gauss(-2, -2, sigma.x);
weight += gauss(-1, -2, sigma.x);
weight += gauss(0, -2, sigma.x);
weight += gauss(1, -2, sigma.x);
weight += gauss(2, -2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-2, -1)) * gauss(-2, -1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-1, -1)) * gauss(-1, -1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -1)) * gauss(0, -1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 1, -1)) * gauss(1, -1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 2, -1)) * gauss(2, -1, sigma.x);
weight += gauss(-2, -1, sigma.x);
weight += gauss(-1, -1, sigma.x);
weight += gauss(0, -1, sigma.x);
weight += gauss(1, -1, sigma.x);
weight += gauss(2, -1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-2, 0)) * gauss(-2, 0, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-1, 0)) * gauss(-1, 0, sigma.x);
fc += texture(sTD2DInputs[0], vUV.st) * gauss(0, 0, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 1, 0)) * gauss(1, 0, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 2, 0)) * gauss(2, 0, sigma.x);
weight += gauss(-2, -0, sigma.x);
weight += gauss(-1, -0, sigma.x);
weight += gauss(0, 0, sigma.x);
weight += gauss(1, -0, sigma.x);
weight += gauss(2, -0, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-2, 1)) * gauss(-2, 1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-1, 1)) * gauss(-1, 1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 1)) * gauss(0, 1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 1, 1)) * gauss(1, 1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 2, 1)) * gauss(2, 1, sigma.x);
weight += gauss(-2, 1, sigma.x);
weight += gauss(-1, 1, sigma.x);
weight += gauss(0, 1, sigma.x);
weight += gauss(1, 1, sigma.x);
weight += gauss(2, 1, sigma.x);
//
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-2, 2)) * gauss(-2, 2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-1, 2)) * gauss(-1, 2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 2)) * gauss(0, 2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 1, 2)) * gauss(1, 2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 2, 2)) * gauss(2, 2, sigma.x);
weight += gauss(-2, 2, sigma.x);
weight += gauss(-1, 2, sigma.x);
weight += gauss(0, 2, sigma.x);
weight += gauss(1, 2, sigma.x);
weight += gauss(2, 2, sigma.x);
// 明るさを一定に保つために行っている。
// 確率密度関数は全体を積分して始めて1.0になるような仕組みになっているため、5x5のフィルタだとすると、どうしてもweightの合計が1未満ninattekuru.
// weightの合計が0.57ぐらいだとすると、1にするために、1/weightをかけてあげて、無理やり調整。
fc *= 1.0f/weight;
//alphaは固定に調整
fc.a = 1.0;
fragColor = TDOutputSwizzle(fc);
}
計算数の軽量化のために、x, yでの計算量を減らしながら似たような結果を得るためのfast gaussian blur
2回にglslを分けて、実装した。
x方向側
uniform vec2 sigma;
out vec4 fragColor;
#define M_PI 3.1415926535897932384626433832795
float gauss1(float x, float sigma){
float exponent = - (x * x) / (2 * sigma * sigma);
float denominator = sqrt(2 * M_PI) * sigma;
return exp(exponent) / denominator;
}
void main()
{
float weight = 0.0f;
vec4 fc = vec4(0);
//x direction
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-5, 0)) * gauss1(-5, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-4, 0)) * gauss1(-4, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-3, 0)) * gauss1(-3, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-2, 0)) * gauss1(-2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(-1, 0)) * gauss1(-1, sigma.x);
fc += texture(sTD2DInputs[0], vUV.st) * gauss1(0, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 1, 0)) * gauss1(1, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 2, 0)) * gauss1(2, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 3, 0)) * gauss1(3, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 4, 0)) * gauss1(4, sigma.x);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 5, 0)) * gauss1(5, sigma.x);
weight += gauss1(-5, sigma.x);
weight += gauss1(-4, sigma.x);
weight += gauss1(-3, sigma.x);
weight += gauss1(-2, sigma.x);
weight += gauss1(-1, sigma.x);
weight += gauss1(0, sigma.x);
weight += gauss1(1, sigma.x);
weight += gauss1(2, sigma.x);
weight += gauss1(3, sigma.x);
weight += gauss1(4, sigma.x);
weight += gauss1(5, sigma.x);
fc *= 1.0f/weight;
fc.a = 1.0;
fragColor = TDOutputSwizzle(fc);
}
y方向側
uniform vec2 sigma;
out vec4 fragColor;
#define M_PI 3.1415926535897932384626433832795
float gauss1(float x, float sigma){
float exponent = - (x * x) / (2 * sigma * sigma);
float denominator = sqrt(2 * M_PI) * sigma;
return exp(exponent) / denominator;
}
void main()
{
float weight = 0.0f;
vec4 fc = vec4(0);
// y direction
weight = 0.0f;
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -5)) * gauss1( -5, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -4)) * gauss1( -4, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -3)) * gauss1( -3, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -2)) * gauss1( -2, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, -1)) * gauss1( -1, sigma.y);
fc += texture(sTD2DInputs[0], vUV.st) * gauss1( 0, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 1)) * gauss1( 1, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 2)) * gauss1( 2, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 3)) * gauss1( 3, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 4)) * gauss1( 4, sigma.y);
fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2( 0, 5)) * gauss1( 5, sigma.y);
weight += gauss1(-5, sigma.y);
weight += gauss1(-4, sigma.y);
weight += gauss1(-3, sigma.y);
weight += gauss1(-2, sigma.y);
weight += gauss1(-1, sigma.y);
weight += gauss1(0, sigma.y);
weight += gauss1(1, sigma.y);
weight += gauss1(2, sigma.y);
weight += gauss1(3, sigma.y);
weight += gauss1(4, sigma.y);
weight += gauss1(5, sigma.y);
fc *= 1.0f/weight;
fc.a = 1.0;
fragColor = TDOutputSwizzle(fc);
}

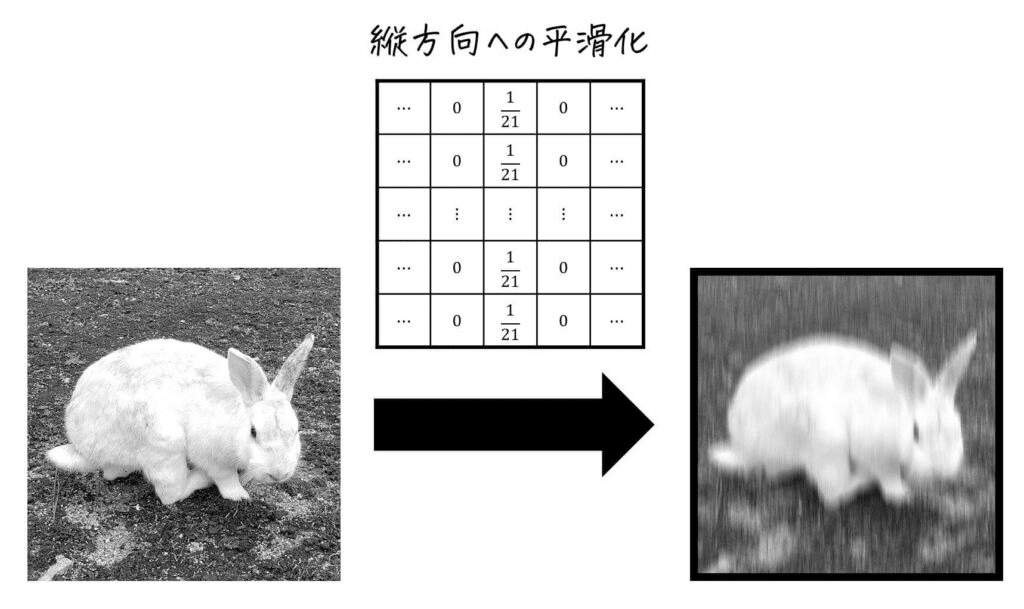
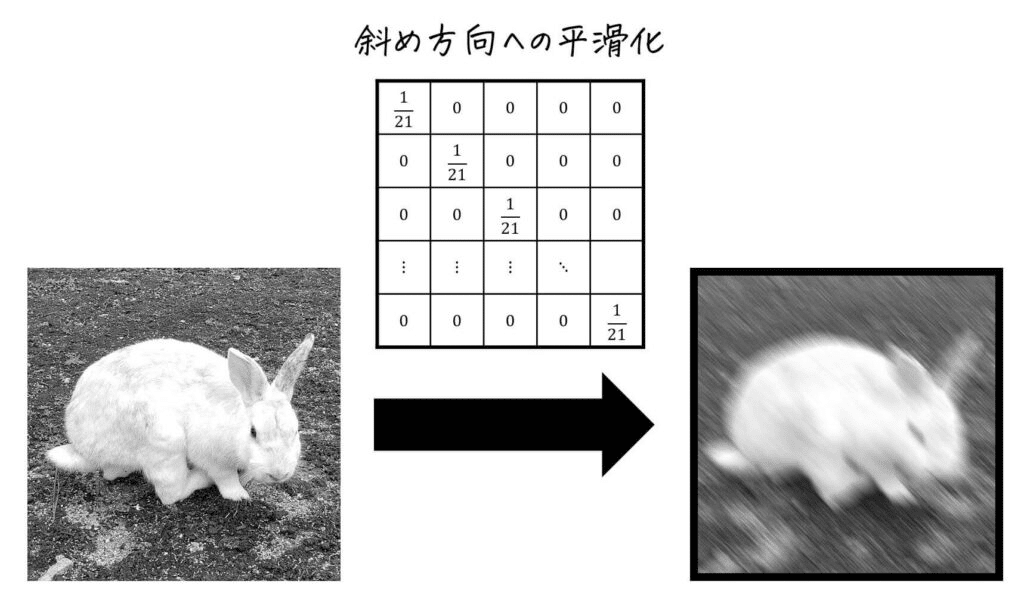
特定方向の平滑化 モーションフィルタ
特定の方向へぼかすような形の平滑化もできる。
フィルターをそのラインに沿った形にすればよい。
雑にモーションブラーのような結果が得られるため、モーションフィルターと呼ばれる場合もある。
方向ブラーと呼ばれる場合もある。



// Example Pixel Sha6
uniform vec2 u_resolution;
out vec4 fragColor;
void main()
{
vec4 fc = vec4(0.0);
for(float i = -8; i <= 8; i++){
for(float j = -8; j <= 8; j++){
if(i == -j){
fc += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y)) * 1/17;
// fc += textureOffset(sTD2DInputs[0], vUV.st, ivec2(i, j)) * 1/81;
}
else{
fc += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y)) * 0;
}
}
}
//alphaは固定に調整
fc.a = 1.0;
fragColor = TDOutputSwizzle(fc);
}
エッジ保存スムージング
Edge preserve filter
[非線形フィルタ]
平滑化により、画像に含まれるノイズなどを軽減できるが、同時に画像に元々あるエッジも滑らかにしてしまう。エッジは保ちつつ、ノイズは減らしたいという方法をここではある。
これらは非線形フィルタに当たる。
選択的局所平均化
基本方針としては、なるべく、画像中のエッジを含まない領域にて、平均化を行うというもの。
つまり、フィルタの窓の形を、都合の良いような形で考えるというもの。
例えば、以下のような5x5のフィルタを考えたとして、図の中王の注目画素を含めて、局所領域を9通り考えてみたとする。その中の画素値の分散が最小になる領域を選び、その領域の平均値を出力するという手法。こうすることで、エッジを避けた領域で平滑化された結果が得られる。

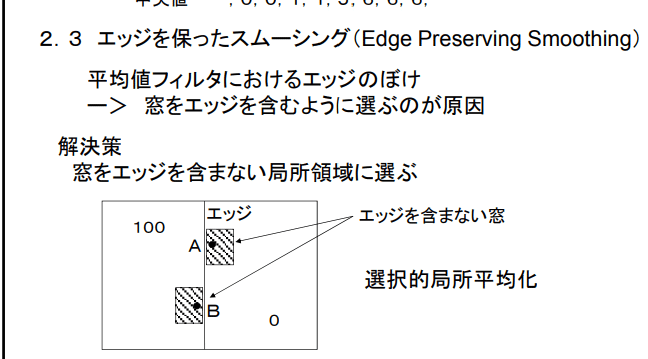
移動平均法と同じく局所領域中の平均濃度を出力値とする方法である。 移動平均法との違いは、局所領域中にエッジを含むかどうか調べエッジを含まない局所領域で平均値を求めることである。これによりエッジをぼかすことなく雑音除去を行える。 ・例として、9個の局所領域(5角形・6角形が4つずつ、正方形が1つ)内の濃度の分散をそれぞれ計 算し、分散が最小になる領域の平均濃度を出力値とする方法がある。 ・計算コストの点では、メディアンフィルタに劣る。
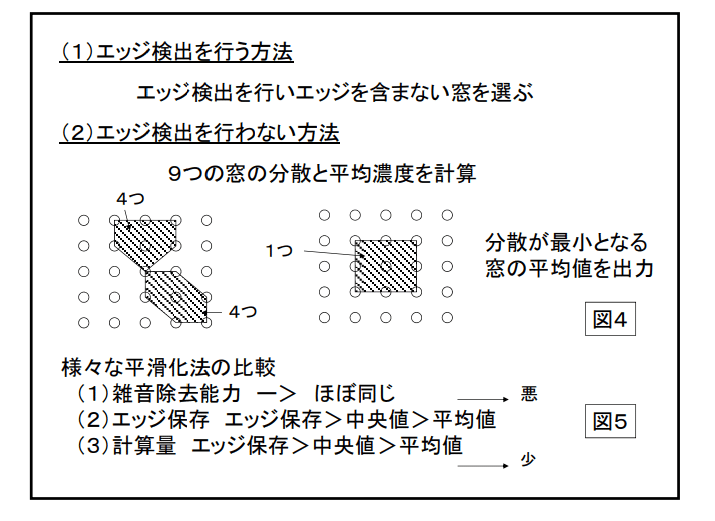
この手法をエッジ保存スムージングと呼ぶケースもある。
k最近隣平均化フィルタ
k-nearest neighbor averaging filter
注目画素の画素値に対して、注目画素の近傍領域中で近い値を持つ画素を一定個数選び出し、その選ばれた画素で平均値を出力とする方法。
つまり、画素値がにている近くの画素はEdgeにならないだろうという考え。
近傍領域の大きさ$${N*N}$$画素、選び出す個数をkとし、$${k \leq \frac{N^2}{2}}$$とすることで、注目画素の画素の値に近い近傍領域中の画素数の半分以下の個数の画素にて平均化するため、画像のエッジがほぞんされやすくなる。
バイラテラルフィルタ
bilateral filter
ガウシアンフィルタは平均化するときにノイズの除去を期待できるが、輪郭のEdgeの部分にも、ブラーがかかってしまうという特徴がある。
この欠点部分を補おうとしているのがこのバイテラルフィルター
edgeの部分を気にしたいため、輝度差があるところが、輪郭という判定を用いて、ガウシアンフィルタをアップデートさせる。
つまり、輝度差の差が大きいところは、フィルタの重みを小さくしようとするモデル。
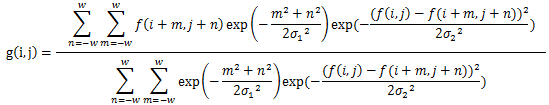
$${W}$$がフィルタのサイズに関わる部分。$${(2W + 1) * (2W + 1)}$$のフィルタサイズを想定。
$${\sigma_1}$$がガウシアンフィルタ側の制御の偏差, $${\sigma_2}$$が輝度差側の制御の偏差
$${\sigma_1}$$の関わる、部分だけを抽出すると以下のような式が取り出せる。
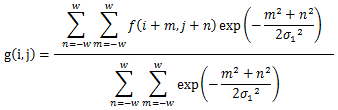
個々の部分だけみると、ガウシアンフィルタと同じもの。
分母に来ている部分はガウシアンフィルタの実装の1/weightしているものと一緒で、重みの合計を1にするための正規化項となっている。
分子部分はそのまんまガウシアンフィルタの部分。
残りの部分を理解するために具体的なエッジの部分を考えてみる
例として、5x5のガウシアンフィルタを当てている場合、中心輝度(注目画素)に近い周辺画素に対しては、1, 輝度差がデカいところには0になるようにしてみる。
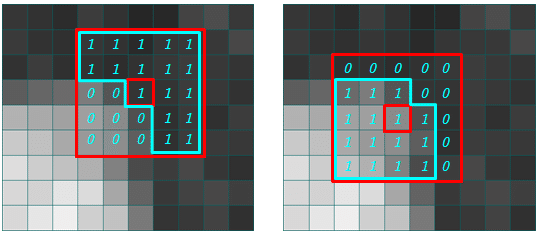
これをガウシアンフィルタの実際の重みに加えると、下記のような形になる。
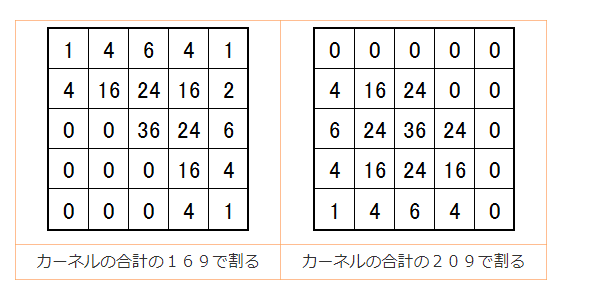
このフィルタを作るために、輝度差が大きいかどうかを判定させるために、正規分布を使う。
つまり、$${f(i,j)}$$で輝度値が返ってくるとして、$${f(i +m, j+n)}$$が周辺画素の輝度値となるため、周辺画素値が中心として、注目画素$${f(i,j)}$$が正規分布においてどのくらいの値を示すかというのを返してくれるのが、下の式の部分。
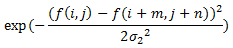
これを分母にもかけてあげることで、正規化項が働いて、結果の重みの合計が1になる。

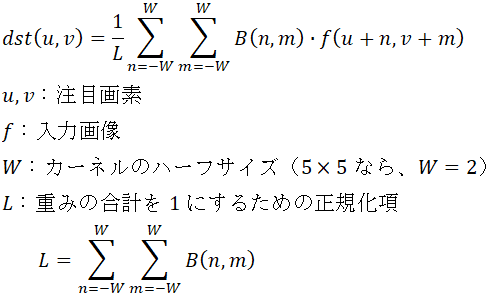
$${\sigma_2}$$の大きさがどのくらいの輝度値までを許容するかという部分を制御しているため、$${\sigma_2}$$を大きくしすぎると、単なるガウシアンフィルタの処理に近づく。
逆に、$${\sigma_2}$$を小さくし過ぎると、全体のフィルタの強さが小さくなってしまうため、ノイズ除去効果も地位sか唸ってしまう。
そこで、実際にはエッジを保持しつつノイズをできるだけ除去したい場合は、1回のバイラテラルフィルタでσ1、σ2の値を調整しようとするよりも、バイラテラルフィルタを何回か繰り返した方が効果的です。

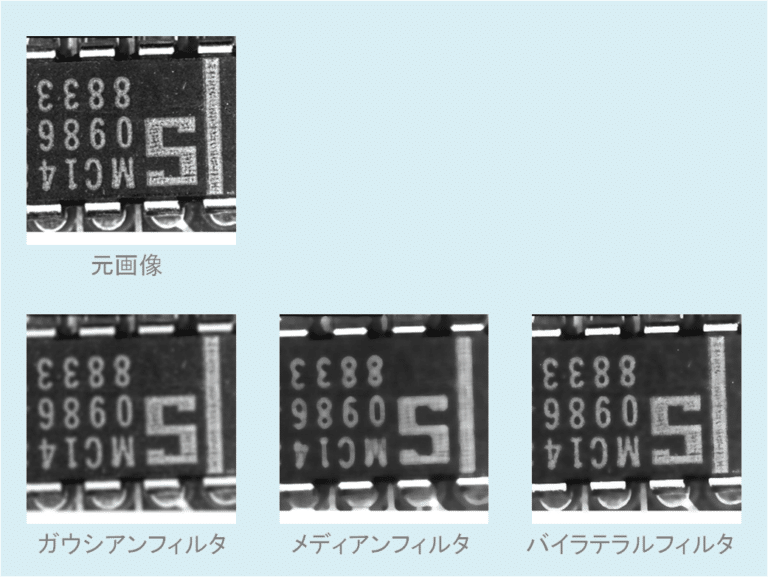
ガウス関数を見ると、カーネル中心からの距離しか考慮されてませんよね?
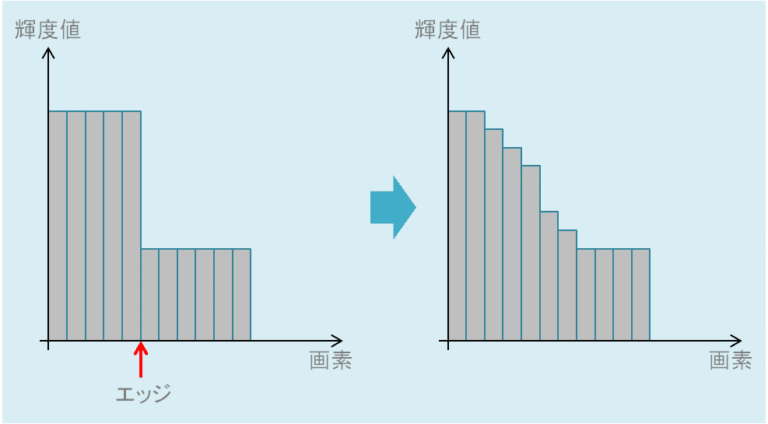
輝度値の差はまったく考慮されていないので、エッジがあるところもないところも同じようにボケてしまいます。
エッジの場所にフィルタを適用する場合、カーネル中心に近いほど大きな重みになるので、そこにエッジがあっても平均化されボケてしまいます。
このように、ガウシアンフィルタではエッジのボケが発生します。
TouchDesignerのGLSLで実装した例。
uniform vec2 u_resolution;
uniform vec2 sigma;
out vec4 fragColor;
vec4 bilateral_1(vec2 sigma, vec2 offset){
vec4 f = texture(sTD2DInputs[0], vUV.st);
vec4 f_ij = texture(sTD2DInputs[0], vUV.st + vec2(offset.x/u_resolution.x, offset.y/u_resolution.y));
float e1 = exp(-(offset.x*offset.x + offset.y*offset.y)/(2 * sigma.x * sigma.x));
vec4 e2 = exp(-((f - f_ij) * (f - f_ij)) / (2 * sigma.y * sigma.y));
vec4 frac1 = f_ij * e1 * e2;
return frac1;
}
vec4 bilateral_2(vec2 sigma, vec2 offset){
vec4 f = texture(sTD2DInputs[0], vUV.st);
vec4 f_ij = texture(sTD2DInputs[0], vUV.st + vec2(offset.x/u_resolution.x, offset.y/u_resolution.y));
float e1 = exp(-(offset.x*offset.x + offset.y*offset.y)/(2 * sigma.x * sigma.x));
vec4 e2 = exp(-((f - f_ij) * (f - f_ij)) / (2 * sigma.y * sigma.y));
vec4 frac2 = e1 * e2;
return frac2;
}
void main()
{
vec4 fc = vec4(0.0f);
vec4 _fc = vec4(0.0f);
int filterSize = 8;
for(float i = -filterSize; i <= filterSize; i++){
for(float j = -filterSize; j <= filterSize; j++){
fc += bilateral_1(sigma, vec2(i,j));
_fc += bilateral_2(sigma, vec2(i,j));
}
}
fc /= _fc;
//alphaは固定に調整/project1/glsl4
fc.a = 1.0;
fragColor = TDOutputSwizzle(fc);
}

トリラテラルフィルタ
Trilateral filter
バイラテラルフィルタを改良したもの。
バイラテラルフィルタでは、空間的距離と画素値としての距離を使用していたが、さらにそこに時間的距離を追加して、動画・映像に対しての画像フィルタになっている。
基本方針はバイラテラルフィルタと一緒で、weightが異なっているイメージ。
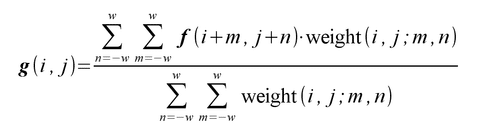
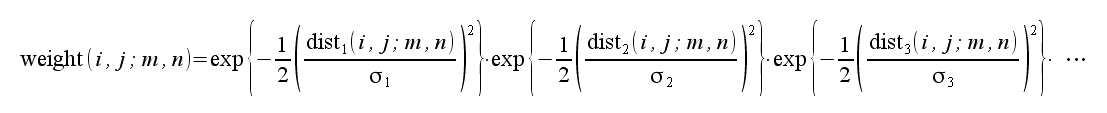
この距離関数に関しては、以下を使う。
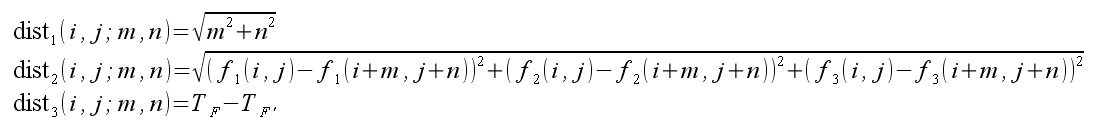
dist1は空間的距離、dist2は色的距離、dist3は時間的距離を示す。
TFは注目している画素を含むシーンの時間、TF'は近傍画素を含むシーンの時間です。
ノンローカルミーンフィルタ
non-local mean filter
バイテラルフィルタではある注目画素に対して、その周辺の画素を用いて平均化する際に、注目画素と周辺画素の画素値の差に応じた重みを用いた
それに足して、注目画素の周りの小領域の画素値パターンと、周辺画素のまわりの小領域の画素値パターンとの間の類似度に応じた重みを用いて、平均化を行う手法。
$$
w(i, j, m, n) = \exp(-\frac{\Sigma^{W'}_{t = -W'} \Sigma^{W'}_{s=-W'} (f(i + s, j+t) - f(i +m+s, j+n+t))^2}{2 (\sigma_3)^{2}})
$$
小領域の大きさは$${(2W' +1) * (2W' +1)}$$の正方形領域で、$${\sigma_3}$$は画素値パターンの類似度に応じた重みを表すガウス分布の標準偏差。
$${w(i,j,m,n)}$$が重みを表していて、
バイテラルフィルタ同様に出力画素を$${g(i,j)}$$とする。
$$
g(i,j) = \frac{\Sigma^{W}_{n = -W} \Sigma^{W}_{m=-W} w(i, j, m, n) f(i+m, j+n)}{\Sigma^{W}_{n = -W} \Sigma^{W}_{m=-W} w(i, j, m, n)}
$$
バイテラルフィルタとは異なり、画素ごとの値の近さではなく、パターンの類似度を重みとして使いたいため、重み付き平均を計算する周辺画素の範囲を大きくしてもあまり画素の劣化が生じない。
そのため、その範囲を画像全体とすることも可能なため、「ノンローカル」の名前がついている。ただ、一般には限定した適当な範囲にした方が良い結果が得られる。
$${w(i,j,m,n)}$$の意味としては、$${f(i+s, j+t)}$$が現在の仮の注目画素で、そこから$${(+s, +t)}$$だけオフセットさせた位置の画素値とのガウス分布をとって、画素値が近いかどうかをガウス分布の重みに沿わせる。それを$${\Sigma}$$で周辺領域回分繰り返して総和を出す。それがその周辺領域での類似度の重みにするという仕組み。
バイラテラルフィルタのように、注目画素からの距離に応じた重みをさらに加えてもよい。
すると$${w(i,j,m,n)}$$は下記のようになる。
$$
w(i, j, m, n) = \exp(-\frac{m^2 + n^2}{2 (\sigma_1)^2}) \exp(-\frac{\Sigma^{W'}_{t = -W'} \Sigma^{W'}_{s=-W'} (f(i + s, j+t) - f(i +m+s, j+n+t))^2}{2 (\sigma_3)^{2}})
$$
uniform vec2 u_resolution;
uniform vec2 sigma;
uniform ivec2 u_filterSize;
out vec4 fragColor;
vec4 nonLocalMean(vec2 sigma, vec2 offset){
int _filterSize = u_filterSize.y;
vec4 numerator = vec4(0.0f);
for(float s = -_filterSize; s <= _filterSize; s++){
for(float t = -_filterSize; t <= _filterSize; t++){
vec4 f_st = texture(sTD2DInputs[0], vUV.st + vec2(s/u_resolution.x, t/u_resolution.y));
vec4 f_msnt = texture(sTD2DInputs[0], vUV.st + vec2((offset.x + s)/u_resolution.x, (offset.y+t)/u_resolution.y));
vec4 p = f_st - f_msnt;
numerator += p*p;
}
}
float exponentGauss = exp(-(offset.x * offset.x + offset.y * offset.y)/(2 * sigma.x * sigma.x));
float denominator = 2 * sigma.y * sigma.y;
return exponentGauss * exp(- numerator / denominator);
}
void main()
{
vec4 fc = vec4(0.0f);
vec4 _fc = vec4(0.0f);
int filterSize = u_filterSize.x;
for(float m = -filterSize; m <= filterSize; m++){
for(float n = -filterSize; n <= filterSize; n++){
fc += texture(sTD2DInputs[0], vUV.st + vec2(m/u_resolution.x, n/u_resolution.y)) * nonLocalMean(sigma, vec2(m,n));
_fc += nonLocalMean(sigma, vec2(m,n));
}
}
fc /= _fc;
//alphaは固定に調整
fc.a = 1.0;
fragColor = TDOutputSwizzle(fc);
}
for文を増やさなくていけない実装になってしまったため、バイラテラルに比べて、各段に処理が重い。
paramterはの調整も状況によってはバイラテラルの方が綺麗に思える場面もあった。


Guidedフィルタ
Guided filter
エッジを残したまま画像を平滑化するためのフィルタです.同系統の効果のあるbilateral filterに比べ,高速に処理を行うことができます
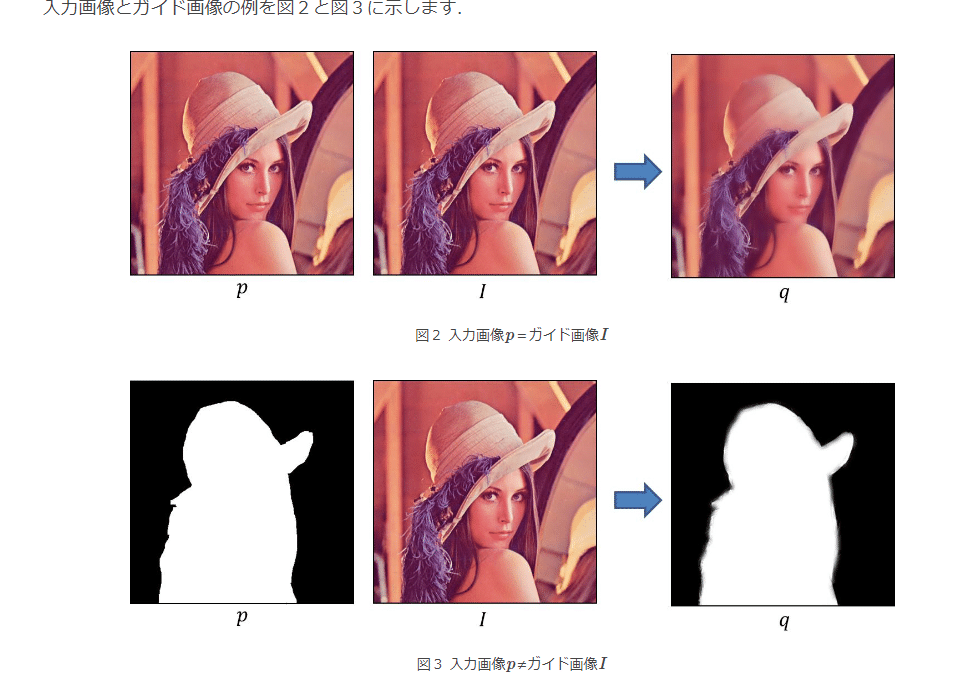
図3の例では,2値のマスク画像を入力画像
p�
として設定します.こうすることで,境界部分の数値を調整した出力画像を作りだすこともできます.
マスク画像は背景差分や手動で設定する方法がありますが,例えば羽毛の部分などのよに単純な2値化がむつかしい箇所があります.そのような場合,まずは概略的にマスク画像を設定して,次にGuided Filterを使って調整する手順が有効です.
bilateral filterでも同じようなことができますが,こちらは処理時間が掛かります.実験結果の比較は文献[1][2]にいくつか説明されていますので参考にしてください.
Domain Transform filter
バイラテラル・フィルタのようなフィルタをエッジ保存型フィルタ(Edge-preserving filter)などと呼び、このエッジ保存型フィルタをより高速に、より高精度にするため様々な研究が現在もされています。
今回紹介する「Domain Transform Filtering」(これは僕が勝手に言ってる名前です)は、フィルタ関数の定義域(domain)をあらかじめ変換(transform)し、エッジ保存型フィルタを線形のフィルタ処理により実現するというものです。
さらにこのアルゴリズムは、フィルタを画像の各行、各列に独立に適用できるので、並列化が容易です。GPUを用いて並列計算すれば、リアルタイムで動かすことも可能でしょう。
今回、私が書いたコードは、論文の中で紹介されている3つのフィルタのうちRecursive filterというもので、繰り返しフィルタを適用することで最終的な処理結果を得るというものです。より詳しい情報がほしい方は、論文をご覧ください。
Joint Bilateral Filter

メディアンフィルタ
median filter
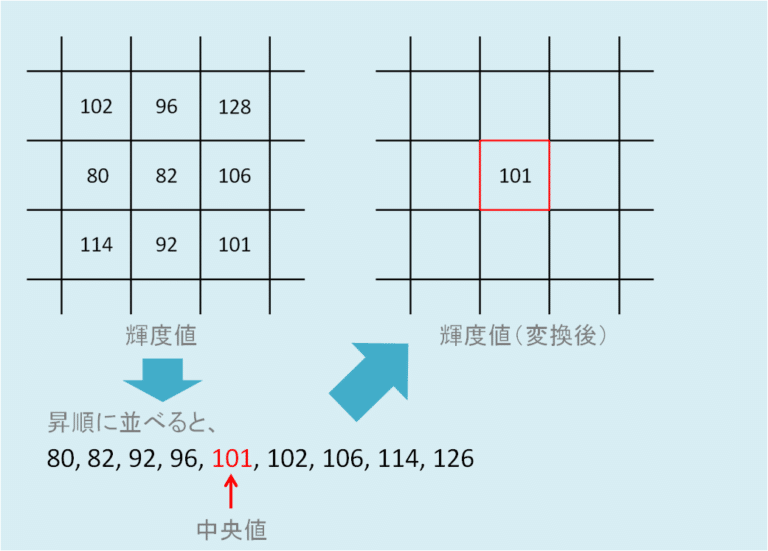
ここまでのものは基本的に画素値の平均を求めるものであったのにたいして、平均値の代わりに中央値(median)を出力として使用するフィルタをメディアンフィルタと呼ぶ。3x3のメディアンフィルタの場合、3x3=9画素の中から中央値を出力とする。特徴として、スパイク上のノイズ(ぷつぷつとした、ノイズ)の除去に効果がある。

「メディアンフィルタ」があります。平均化フィルタはある領域内の平均値を出力するのに対し、メディアンフィルタはある領域内の中央値(メディアン)* を出力するものです。
*中央値(メディアン):領域の画素値を明るい(または暗い)順に並べ替えたとき、ちょうど真ん中に位置する値
平均化フィルタを適応すると全体的に画像がぼやけてしまい、エッジが鈍ってしまうのに対し、メディアンフィルタは画像のエッジへの影響を比較的押さえながらノイズを除去することができます。特に、画像中のランダムなノイズ(スパイクノイズなど)を除去する際に効果を発揮するものです。
両面フィルター、ガイド付きフィルター、異方性拡散フィルター、桑原フィルター
エッジの抽出
edge extraction
画像の中で明るさが急に変化する部分 = エッジ部分の抽出鵜を行うためのフィルタ。
画像中から特徴や図形を検出するための前処理などにも使われる。
微分フィルタ
連続関数$${f(x)}$$の微分は、微分可能であれば、$${h \rightarrow +0}$$)(右側から微分), $${h \rightarrow -0}$$(左側から微分)の極限値は等しくなる。対して、ディジタル画像の場合、注目が外その隣接が外の差分で置き換えられるが、その隣接画素を右側に取るか、左側に取るかによって、一般には差分の値が異なる。
そのため、微分フィルタにはいくつかの種類が考えられる。
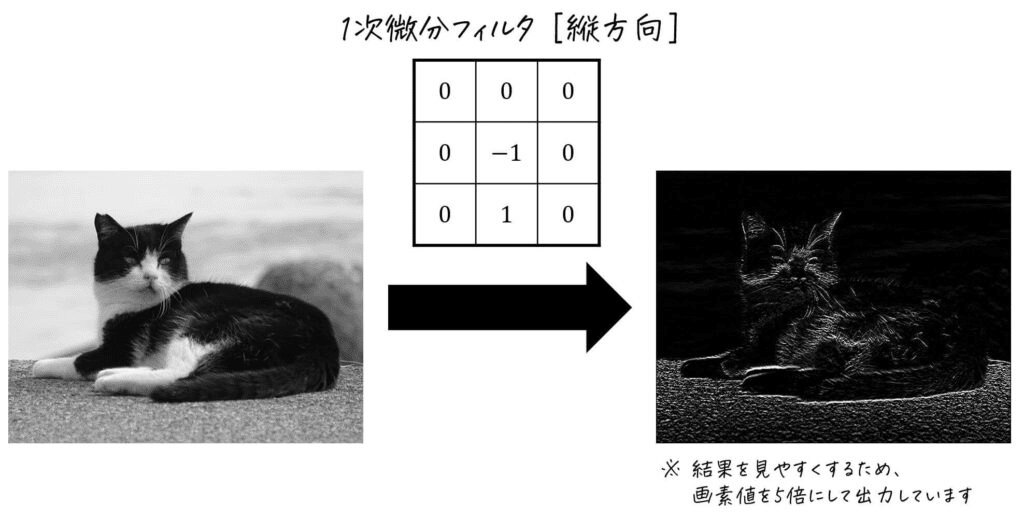
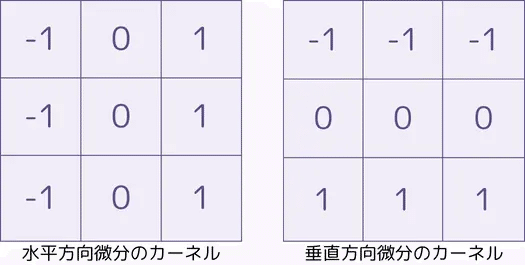
下記の画像の例でいう一番左上では、注目画素とその左隣の画素との差を出力するフィルタ。その右隣りのフィルタは、右隣の画素との差を出力、さらに右隣のフィルターは左右両方の差分値の平均を取って注目画素の微分値とす考え方。
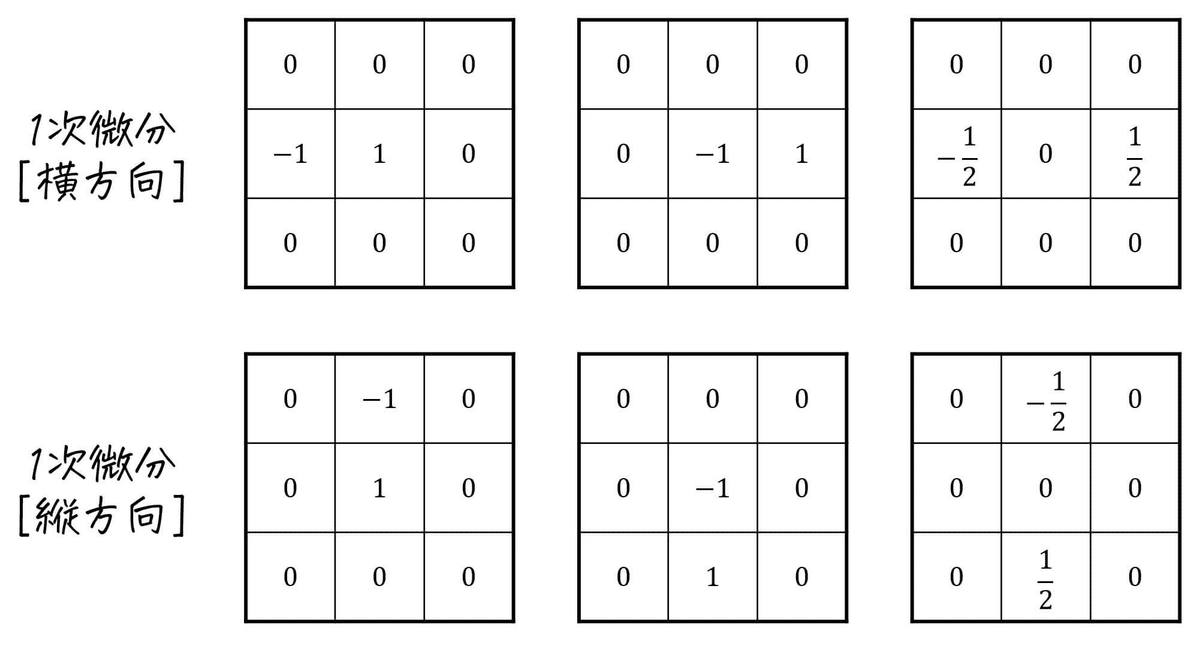
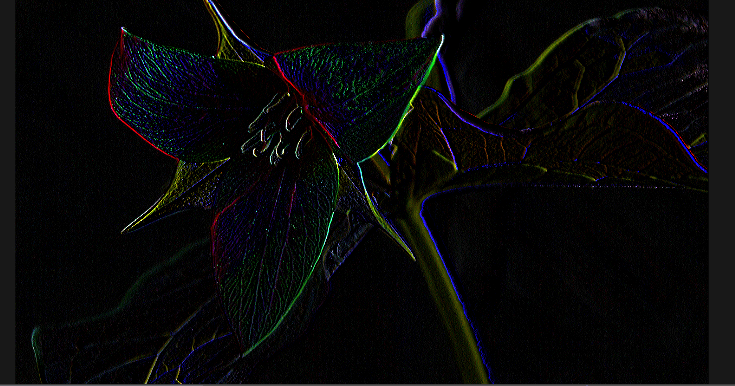
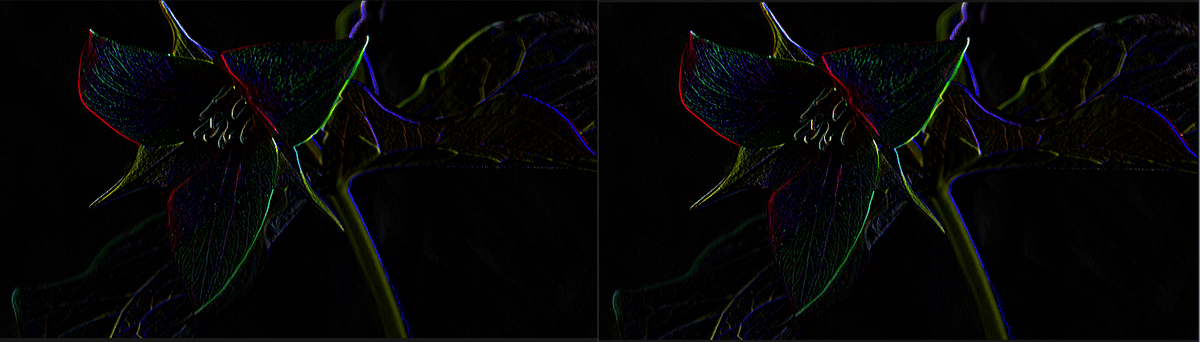
これらのフィルタでは横方向の差分をも止めるようなものため、画像の縦方向のエッジが強く出ていることが確認できる。

fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)) * 1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 0/u_resolution.y)) * -1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)) * 0;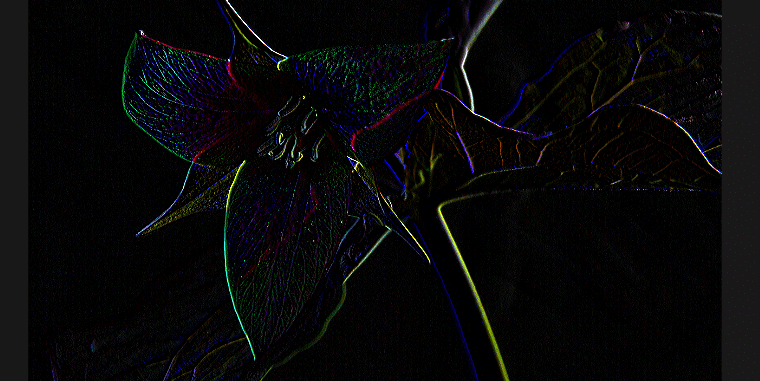
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 0/u_resolution.y)) * -1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)) * 1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)) * 0;逆に縦方向の微分(差分)を求めるようなフィルタの場合は、横方向のエッジが強く出る傾向にある。
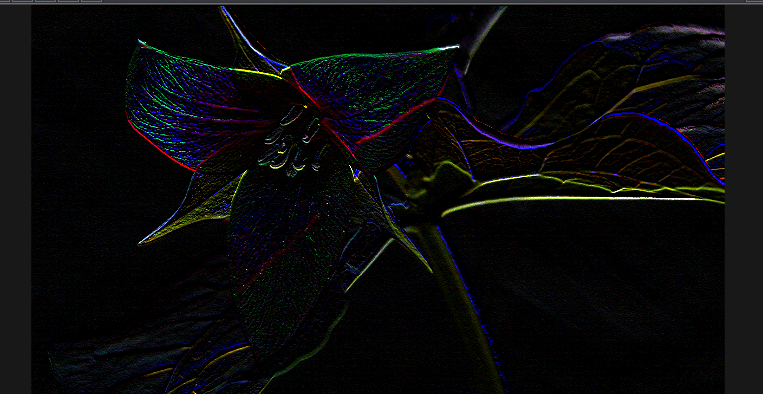
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)) * 1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 0/u_resolution.y)) * -1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)) * 0;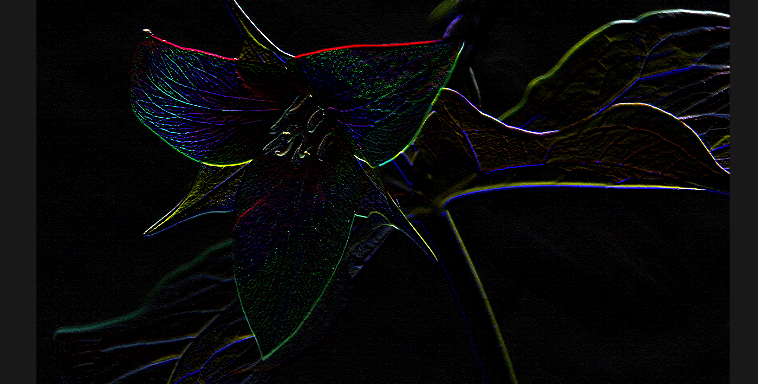
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 0/u_resolution.y)) * -1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, -1/u_resolution.y)) * 1;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)) * 0;
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)) * 0;
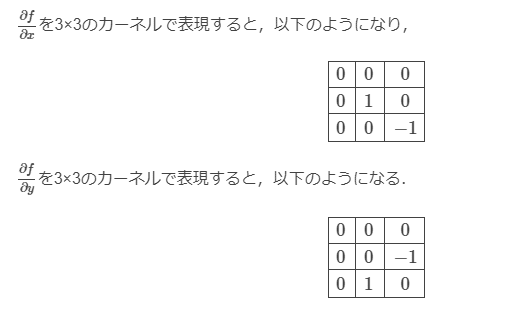
fc += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)) * 0;各画素の横方向の差分を$${\Delta_x f(i,j)}$$、縦方向の差分を$${\Delta_y f(i,j)}$$としたとき、
$${(\Delta_x f(i,j), \Delta_y f(i,j))}$$は画素値の勾配を表す。
また勾配の大きさと方向は
$$
\sqrt{(\Delta_x f(i,j)^2, \Delta_y f(i,j)^2)}
$$
$$
\tan^{-1}{\frac{ \Delta_y f(i,j)}{(\Delta_x f(i,j)}}
$$
ロバーツフィルタ
Roberts filter
斜め方向に微分フィルタを施すフィルタ。


プリューウィットフィルタ
Prewitt filter
微分フィルタでは画像の濃淡が急激に変化するエッジの部分を抽出できるが、同時に画像中のノイズも強調させてしまう。
ノイズもエッジと判定できてしまうため。
ノイズを抑えながらエッジを抽出するため以下のようなことを考える。
入力画像 > 横方向微分フィルタ > 縦方向平滑化 > 出力画像
つまり、横方向のエッジを抽出する場合、それと直交する縦方向に関しての平滑化を行う。
そうすることで、縦方向のエッジは残しつつノイズを低減させるという試み。
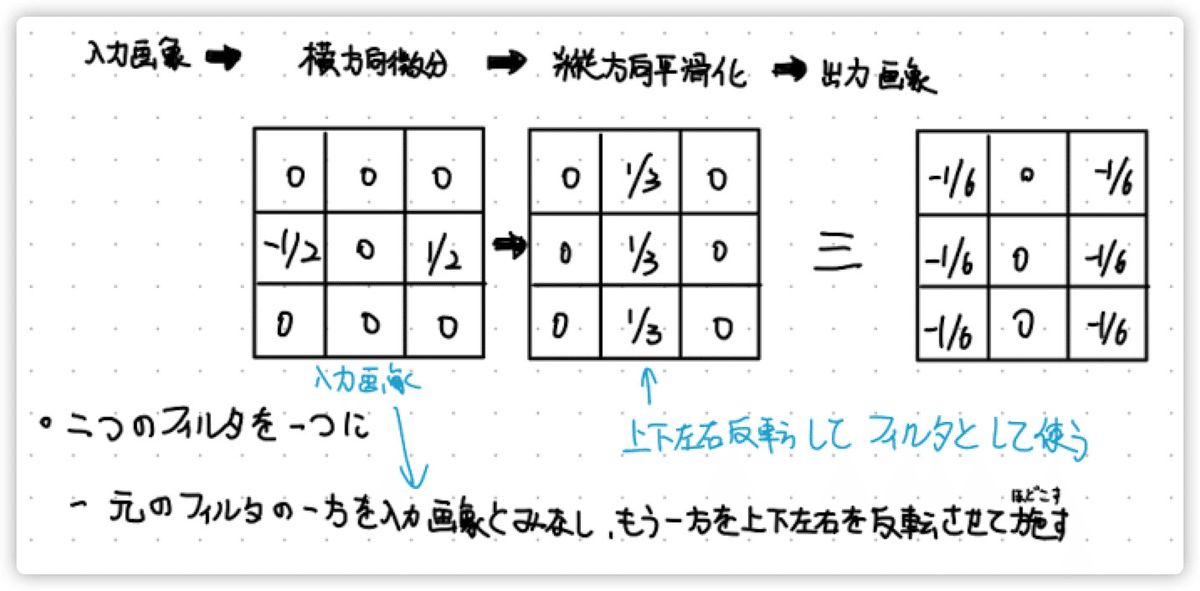
上記のように、右のようなフィルタが等価として考えられる。
微分フィルタの方を入力画像だと考えて、$${frac{1}{3}}$$の方のフィルタを適用させると右のようなフィルタが出来上がる。
上図の$${\frac{1}{6}}$$の掛け算を除いて、整数値だけで表される状況をプリューウィットフィルタと呼ばれている。つまり、プリューウィットフィルターの出力は通常微分値の6倍に相当する値になる。
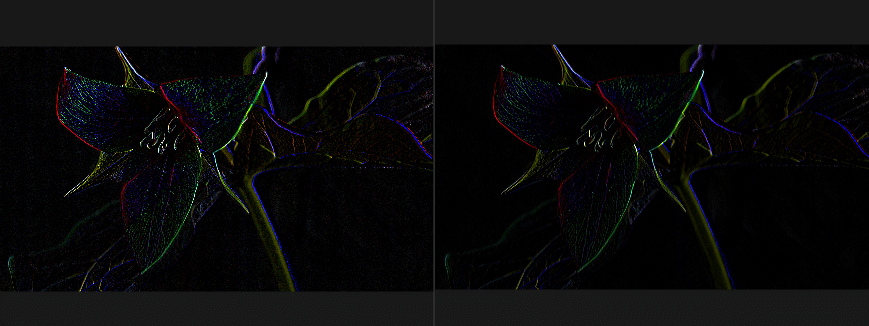
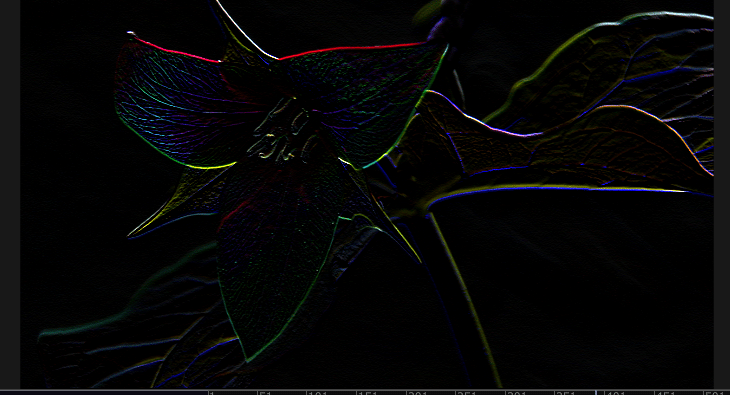
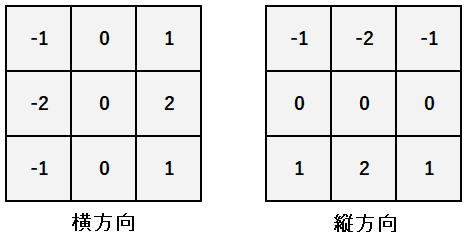
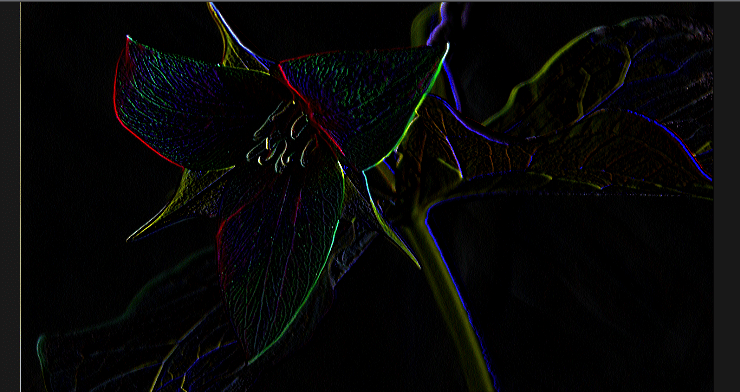
ソーベルフィルタ
sobel filter
さらに、先ほどのプリューウィットの縦方向の平滑化のときに、重み付き平均化を使う場合を考えてみる。
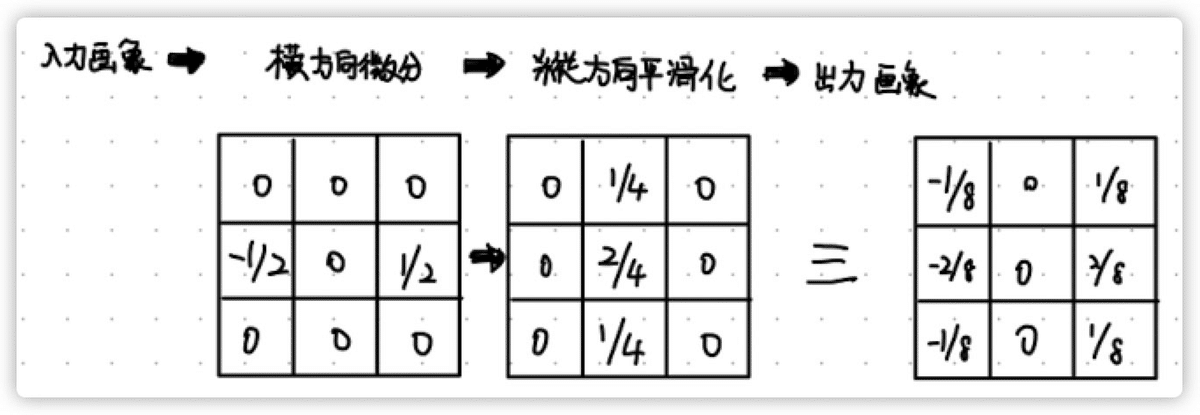
同様に、右のフィルタが等価フィルタとなる。1/8の掛け算を除いた整数値のフィルタがソーベルフィルタと呼ばれる。
よって、ソーベルフィルタの出力は通常の微分値の8倍に相当する値となる。
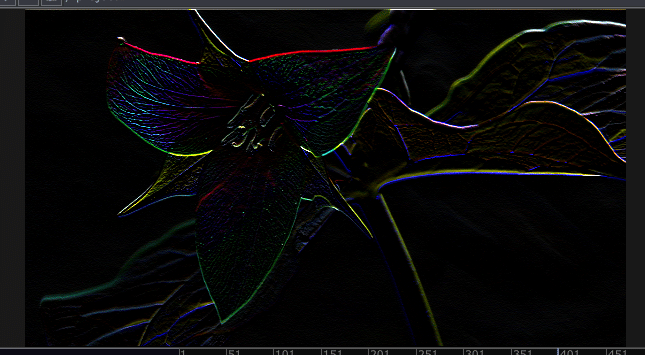
ラプラシアンフィルタ
Laplacian filter
微分フィルタはいうなれば、1次微分に相当するものだったが、
ここでは2次微分に対応する処理を行ってみる。
単には微分を2回繰り返すことであるため、ディジタル画像においては、差分を二回繰り返してみたらよい。
1次微分フィルタは厳密に考えると、それぞれ注目画素の右と左に半画素ずれた位置の差分値を求めていると解釈できる。
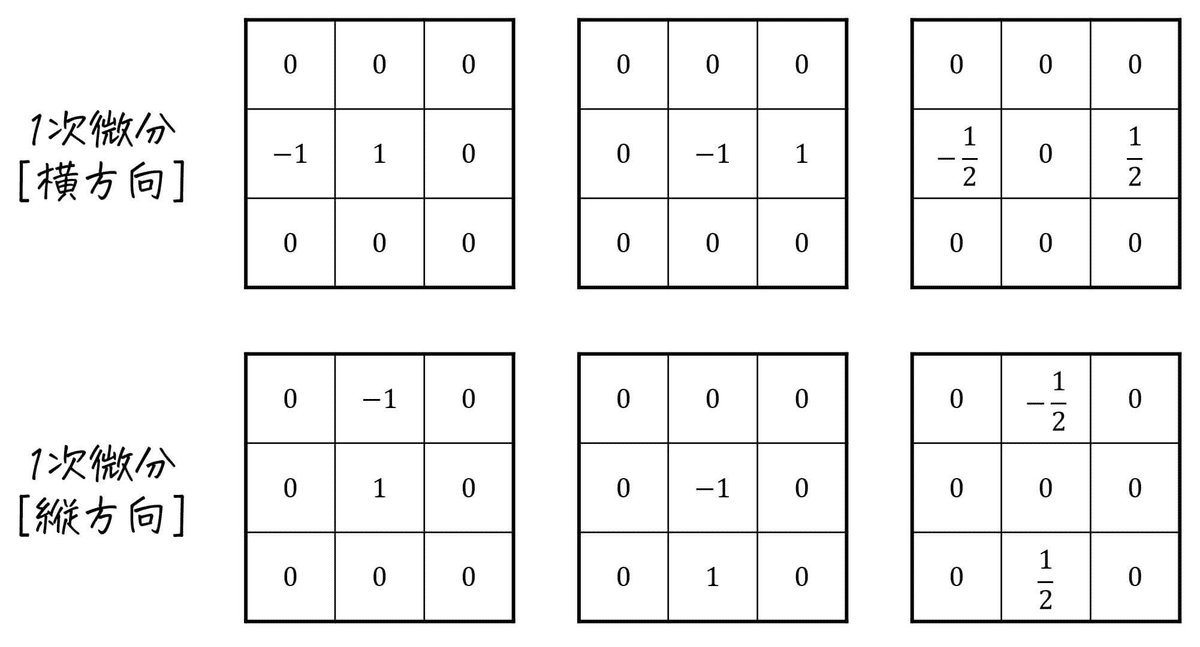
そこでそれぞれのフィルタの出力の差を求めれば、ちょうど注目画素の位置の二回微部分を求めることとなる。
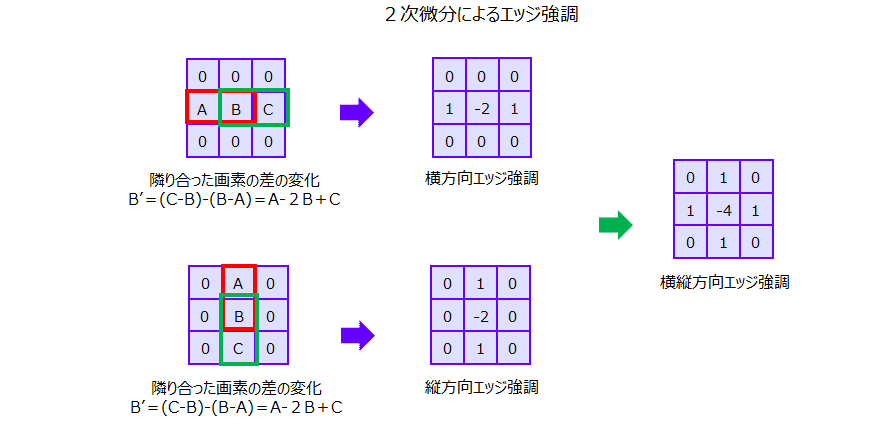
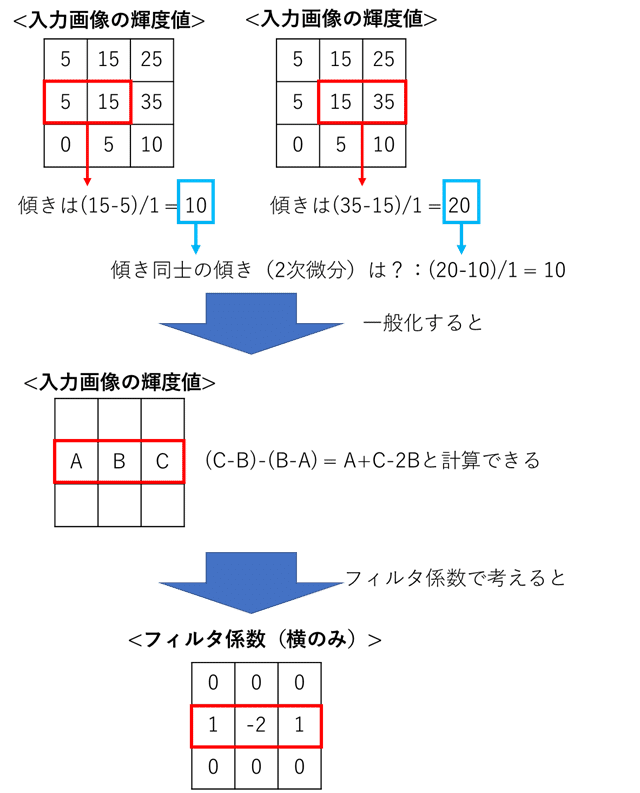
これを縦横どちらもの2階微分の結果を足し合わせて求めることでラプラシアンの値が求められて、縦横のエッジが得られる。
一般に関数$${f(x,y)}$$のラプラシアンは以下で定義される。
$$
\frac{\partial^2}{\partial x^2} f(x,y) + \frac{\partial^2}{\partial y^2} f(x,y)
$$
上記のようなラプラシアンフィルタは4近傍ラプラシアンフィルタと呼ばれ、縦横方向のエッジの抽出が行える。8近傍ラプラシアンフィルタと呼ばれるものはそこにされらに、斜め方向も追加したもの。
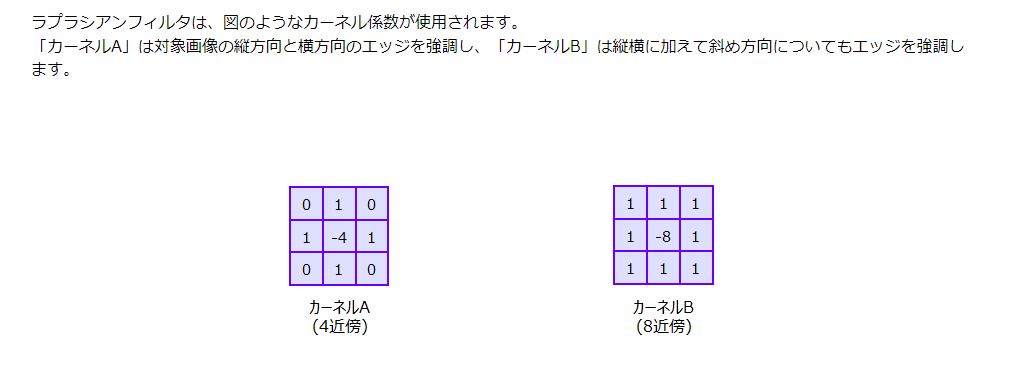
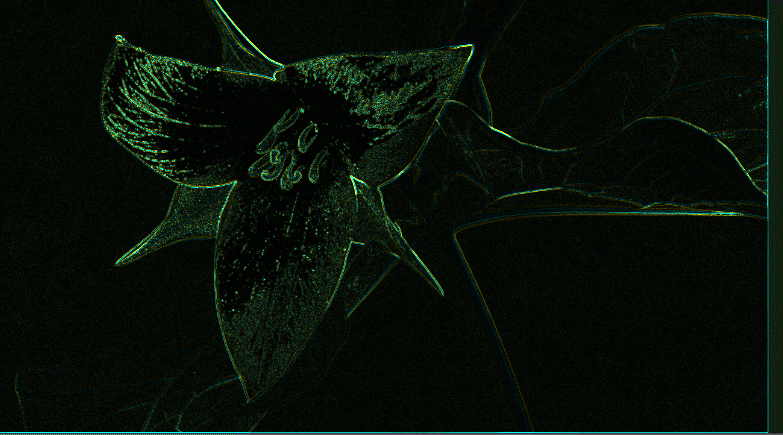
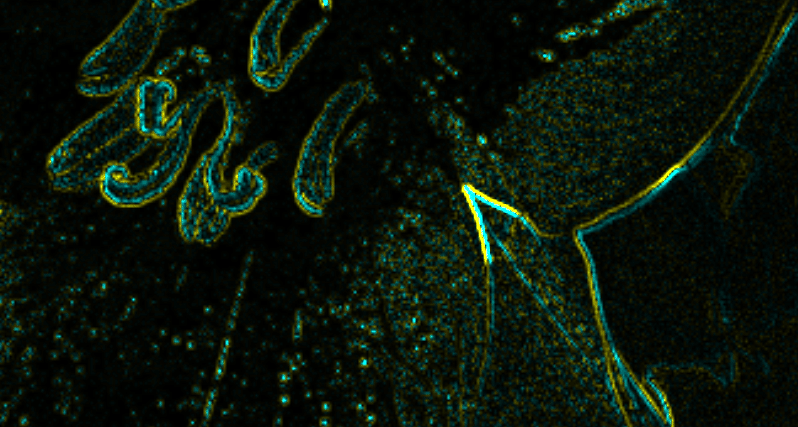
ラプラシアンフィルタでは、方向に依存しないエッジが得られるため、プラスの値と、マイナスの値が得られる。
gチャンネルのみを活かしたとして、gチャンネルが+だったらyellow, -だったらcyanに色づけるとしたら以下のような画像が出来上がる。

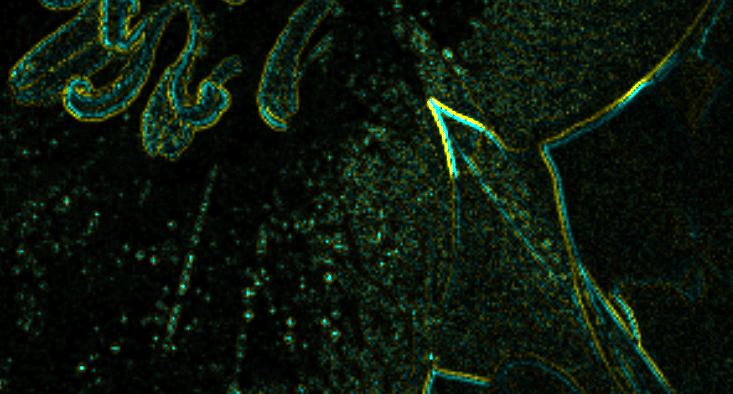
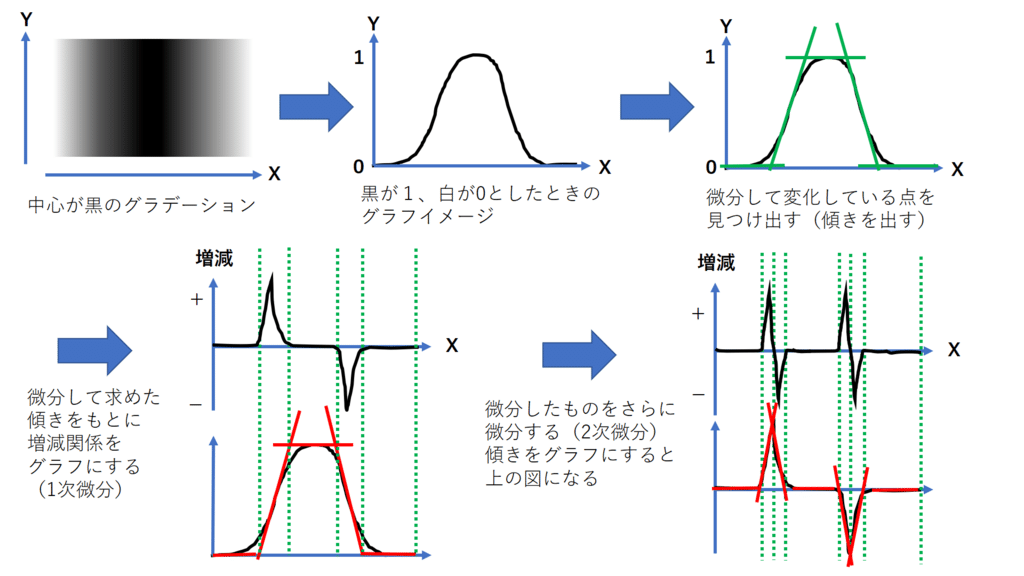
基本的に、エッジの位置をはさんで+/-の値が対になって表れる傾向がある。理由は、二階微分のグラフを考えてみると、エッジの位置に+/-が対になって表れることが分かる。つまり、エッジの正確な位置を求めたければ、値が+から-, -から+へ変化する間のちょうど0になる地点(ゼ4ロ交差(zero crossing))を求めて、それをエッジ位置とすれば求まる。
ただし、ラプラシアンは本質的には微分をくりかえしているため、ノイズを強調してしまう。
LoGフィルタ
Laplacian of Gaussian filter
ラプラシアンは本質的には微分をくりかえしているため、ノイズを強調してしまう。
そのため、まずガウシアンフィルタを適用して、平滑化を行ったのち、ラプラシアンフィルタを適用する方法が取られるケースが多い。
これらの2つの処理は1つにまとめて表すケースが多いため、2次元ガウス分布のラプラシアンを計算すると以下のようになる。
$$
h_g(x,y) = \frac{x^2 + y ^ 2 - 2 \sigma^2}{2\pi\sigma^6}\exp(-\frac{x^2+y^2}{2\sigma^2})
$$
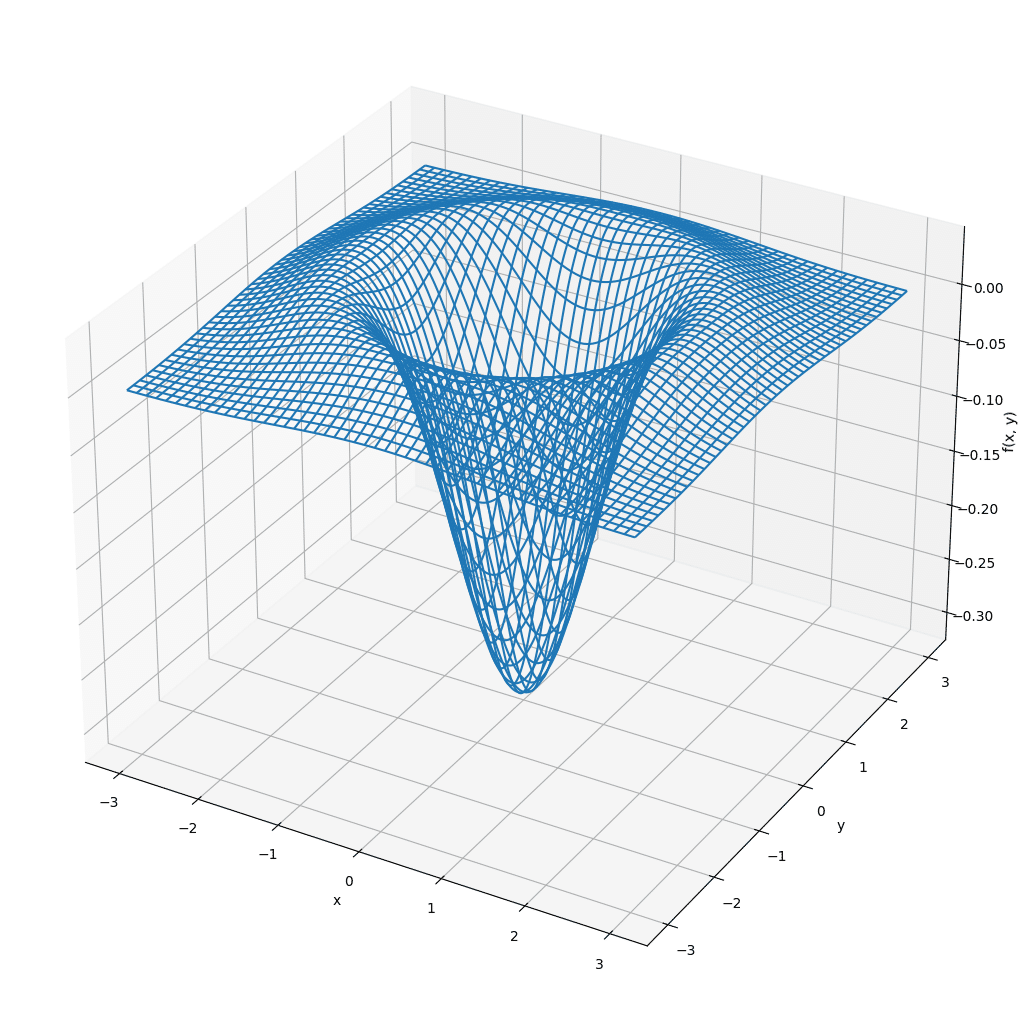
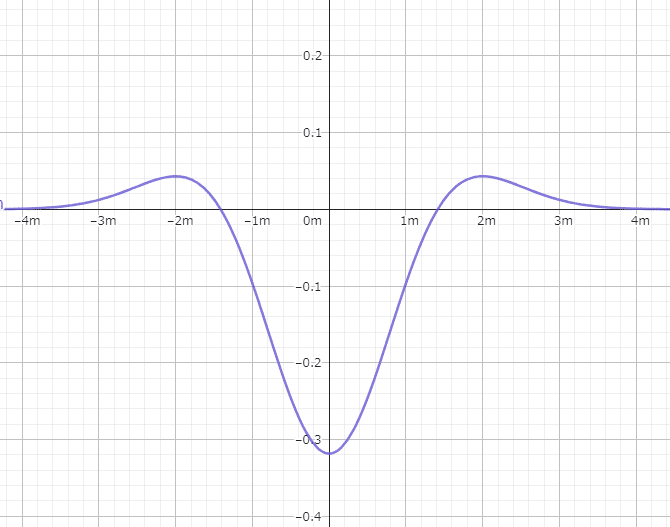
= x軸に沿った断面のグラフ
$${x=0, y=0}$$の地点の最小値に当たる部分が$${-\frac{1}{\pi \sigma^4}}$$を示し、上記のグラフで言う横軸の切片部分が、$${\pm \sqrt{2}\sigma}$$となっている。
この$${h(x,y)}$$を係数とするフィルタをあらかじめ用意して処理するケースがある。このようなフィルタをLoG(Laplacian of Gaussian)フィルタと呼ぶ。
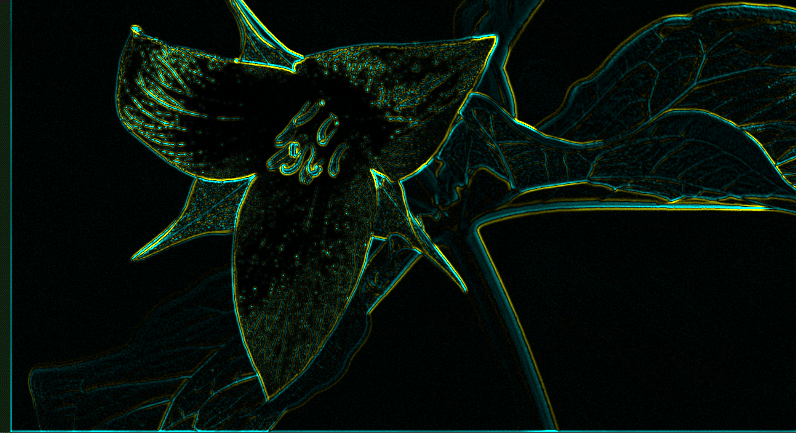
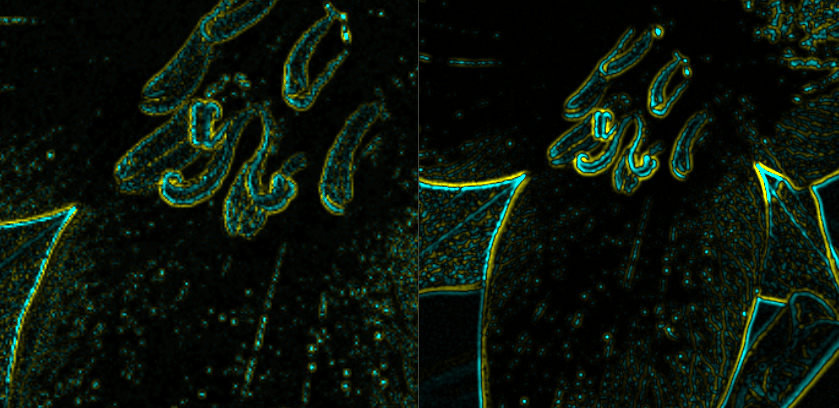
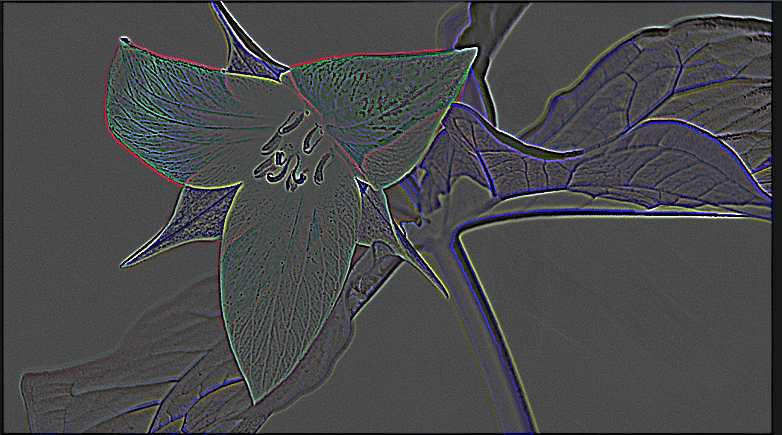
$${\sigma = 1.2}$$

$${\sigma}$$の値を適当に調整することにより、画像から抽出する対象の構造の細かさを選択することができる。
また、ゼロ交差の結果は入力画像のエッジが存在していない子部分も抽出されるが、勾配の大きさが小さいゼロ交差を除くという処理を追加すれば、それらは除くことができる。
uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
uniform float sigma;
out vec4 fragColor;
#define M_PI 3.1415926535897932384626433832795
float LoG_filter(vec2 offset){
float numerator = offset.x * offset.x + offset.y * offset.y - 2 * sigma * sigma;
float exponent = exp(- (offset.x * offset.x + offset.y * offset.y) / (2 * sigma * sigma));
float denominator = 2 * M_PI * pow(sigma, 6);
return numerator/denominator * exponent;
}
void main()
{
vec4 fc = vec4(0.0f);
float _fc = 0.0f;
int filterSize = 4;
for(int i = -filterSize; i <= filterSize; i++){
for(int j = - filterSize; j <= filterSize; j++){
fc += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y/)) * LoG_filter(vec2(i,j));
//_fc += LoG_filter(vec2(i,j));
}
}
// fc /= _fc;
fc *= adj.x;
//alphaは固定に調整
fc = vec4(fc.g);
fc.a = 1.0;
//
// if(fc.g >= 0){
// fc = vec4(fc.g, fc.g, 0.0f, 1.0f);
// }
// else{
// fc = vec4(0.0f, -fc.g, -fc.g, 1.0f);
// }
// 0をグレーに
// fc += adj.y;
//zero crossing
if(fc.g >= -adj.z && fc.g <= adj.z){
fc = vec4(vec3(1.0f), 1.0f);
}
else{
fc = vec4(vec3(0.0f), 1.0f);
}
fragColor = TDOutputSwizzle(fc);
}
DoG (Difference of Gaussian)
(Difference of two Gaussian)
LoGの重たい処理を$${\sigma}$$の異なる2つのガウシアンの差分によって近似した軽量化フィルタ
$$
DoG(x, y) = G(x, y, \sigma_1) - G(x, y, \sigma_2)
$$
ラプラシアンの逆凸のような形を作れる。
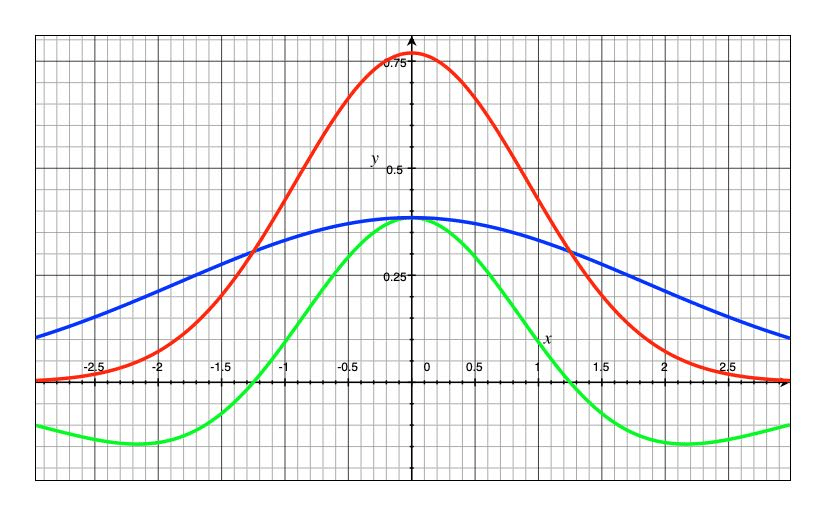
赤と青が分散の違う2つのガウシアン関数,緑がその差をとったグラフです.
ガウシアンフィルタはフィルタの総和が1になるように調整されているので,差分を取ると総和は0となります.
周辺画素の値と対象画素の値の差が小さい(エッジがない)と0に近づき,大きい(エッジがある)と適用後の値も大きくなります.
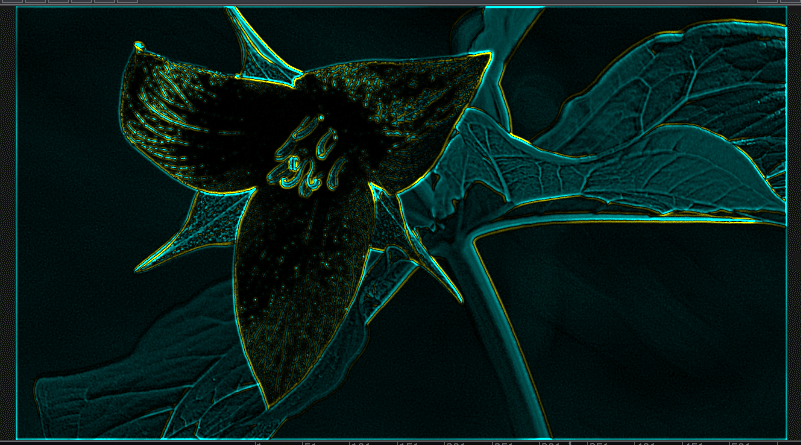
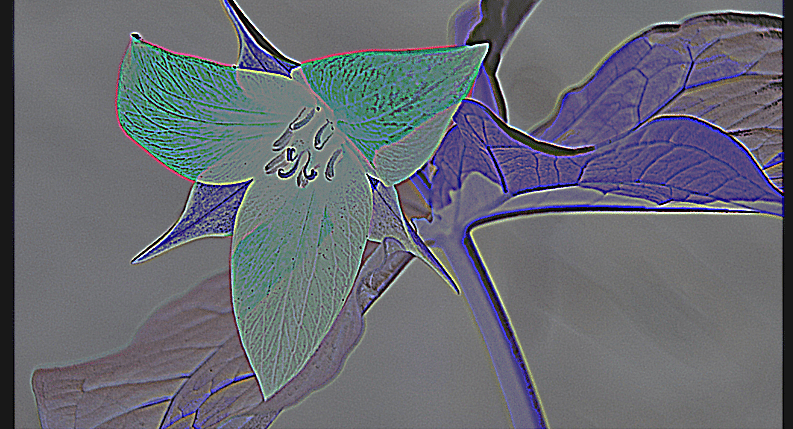

ゼロ交差の調整が独立してもっと詰めた方がよさそう。
uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
uniform vec2 sigma;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float gauss(float x, float y, float sigma){
float exponent = - (x * x + y * y) / (2 * sigma * sigma);
float denominator = 2 * M_PI * sigma * sigma;
return exp(exponent) / denominator;
}
void main()
{
vec4 fc = vec4(0.0f);
vec4 _fc = vec4(0.0f);
vec4 __fc = vec4(0.0f);
int filterSize = 4;
for(int i = -filterSize; i <= filterSize; i++){
for(int j = - filterSize; j <= filterSize; j++){
float DoG = gauss(i, j, sigma.x) - gauss(i,j, sigma.y);
fc += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y)) *DoG;
// _fc += LoG_filter(vec2(i,j));
}
}
// fc /= _fc;
fc *= adj.x;
_fc = fc;
__fc = fc;
//alphaは固定に調整
fc = vec4(fc.g);
fc.a = 1.0;
//
if(fc.g >= 0){
fc = vec4(fc.g, fc.g, 0.0f, 1.0f);
}
else{
fc = vec4(0.0f, -fc.g, -fc.g, 1.0f);
}
fragColor1 = TDOutputSwizzle(fc);
// 0をグレーに
_fc += adj.y;
_fc.a = 1.0f;
fragColor2 = TDOutputSwizzle(_fc);
//zero crossing
if(fc.g >= -adj.z && fc.g <= adj.z){
fc = vec4(vec3(1.0f), 1.0f);
}
else{
fc = vec4(vec3(0.0f), 1.0f);
}
fragColor3 = TDOutputSwizzle(fc);
}
キャニーエッジ検出器
Canny Edge Detector
Cannyエッジ検出器 (Canny Edge Detector) とは,コンピュータビジョンで用いられる古典的な画像エッジ特徴の検出アルゴリズムである [Canny 1986].微分フィルタを用いるだけの単純なエッジ検出と異なり,一筋に連なっった1画素幅のエッジ群を抽出できる.
CannyEdge検出器の利点は,抽出されたエッジは物体境界を含んでいることが多く,その後の高次な認式処理に用いやすいエッジ特徴になっているところにある.それまでは,SobelフィルタやPrewittフィルタで抽出していた生なエッジと比べると,Cannyエッジ検出器は綺麗に連なっていて1画素幅のエッジを抽出できる.
その後に,機械学習ベースのバウンダリー検出手法に取ってかわられるまで(例:probability boundary detector [Martin et al., 2004]] など),エッジ特徴抽出のファーストチョイスとしてCannyエッジ検出器は重宝された.
ステージ1「エッジ方向ごとの細線化」:
勾配の強度(図1-b)と勾配の方向をもとに,法線方向でのNMS(非極大値抑制)(局所範囲での最大値)をおこなう
それにより,幅が広い状態であったエッジを,1画素幅へ細線化(thinning)した「エッジ候補」群を計算する.
ステージ2「ヒステリシス閾値処理」:
ユーザーが設定した2個の閾値を用いて,ステージ1の出力の「エッジ候補」を,「弱エッジ(エッジとしての信頼度低い)」と「強エッジ(エッジとしての信頼度高い)」と「それ以外」に3分類する(図1-c).
そして「弱エッジ」のうち,周りに強エッジがあるものだけ,連結成分処理により「強エッジ」に連結して吸収させる(図1-d).これにより,最終的なエッジを得る.

1画素幅のedgeを検出できる。
大きく5partに分かれて処理される。
まず前処理として、ガウシアンフィルタでノイズを平滑化して、ノイズを減らす。元画像を$${s}$$としたとき、ガウシアンフィルタで平滑かした$${G}$$を計算する。
平滑化したものから、sobelフィルタを用いて、x方向の微分画像$${G_x}$$とy方向の微分画像$${G_y}$$を計算する。
次の準備として、勾配の大きさ(magnitude of gradient)の画像$${M}$$と勾配の方向(orientation of gradient)の画像$${O}$$を$${G_x, G_y}$$から算出。
$${M(i,j) = \sqrt{G_x(i, j)^2 + G_y(i, j)^2}}$$
勾配$${O(x,y)}$$は角度が返ってくるため、エッジに対しての法線方向になる。ここまでは、ラフなエッジをエッジを算出しただけなので、エッジの幅が大きい「稜線(ridge)」状態になっているものが多い
幅の太いエッジの中心をとおる点を繋いだ細いエッジを抽出したい。ここでは、このラフなエッジを縮ませて、1画素幅に細線化させる。
勾配方向上のNMS(Non- maximum suppression, 非極大抑制)という手法で行う。
勾配方向(エッジの法線方向)の狭めの範囲内で、勾配が$${M(i,j)}$$最大値になる座標を探し、その座標以外の全てのエッジは破棄する。
つまり、注目画素とエッジの勾配方向に隣り合う2つの画素値を比較して、画素値が最大でない場合、画素値を0に置き換える。
この、勾配方向にある画素へのアクセスを簡単にするために、4方向[0°, 45°, 90°, 135°]に限定して離散化して考えると処理的には楽。
より正確に、連続値の$${O(i, j)}$$のまま行いたい場合は、連続値のまま内挿・補間したサブピクセルを作り出してサブピクセル位置で補完したMagnitudeの値で極大値探索を行う。細線化されたエッジは各エッジがバラバラの位置にバラバラの強度として出力されている。それらの各エッジのうち、強度が高いものを信頼できるものとして、最終結果として出力する。強度の低い信頼度の低いエッジも強度の高いエッジに接続させることで長く連なったエッジを作りたい。
そこで、勾配の強度値を2つの閾値$${\lambda_{low}, \lambda_{high}}$$をヒステリシス(調節範囲の境界値)として用いて、輝度値を3分割するヒステリシス閾値値処理(Hysteresis Thresholding)を行う。
$${I(x,y) < \lambda_{low}}$$の場合、信頼性の低いエッジ
$${\lambda_{low} \leq I(x,y) \leq \lambda_{high} }$$の場合、信頼性の高いエッジが隣にあれば信頼性の高いエッジとする。なければ信頼性の低いエッジとする。
$${\lambda_{high} < I(x,y)}$$の場合、信頼性の高いエッジ
信頼性の低いエッジは除去する。同時にこれにて、途切れてしまっている輪郭をつなげることができ、誤検出したエッジを削除することができる。



uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
uniform vec2 sigma;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float gauss(float x, float y, float sigma){
float exponent = - (x * x + y * y) / (2 * sigma * sigma);
float denominator = 2 * M_PI * sigma * sigma;
return exp(exponent) / denominator;
}
void main()
{
vec4 fc = vec4(0.0f);
vec4 weight = vec4(0.0f);
vec4 __fc = vec4(0.0f);
int filterSize = 4;
//gauss
for(int i = -filterSize; i <= filterSize; i++){
for(int j = - filterSize; j <= filterSize; j++){
fc += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y)) *gauss(i, j, sigma.x);
weight += gauss(i, j, sigma.x);
}
}
fc /= weight;
// fc.a = 1.0f;
fragColor1 = TDOutputSwizzle(fc);
}
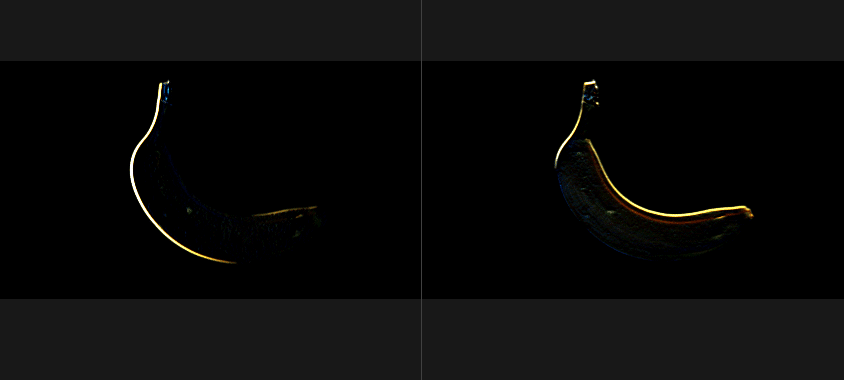
uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
void main()
{
vec4 Gx = vec4(0.0f);
// vec4 weight = vec4(0.0f);
vec4 Gy = vec4(0.0f);
// int filterSize = 4;
//sobel Gx
Gx += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)) * 0;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)) * 1/2;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)) * 0;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)) * 0;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 0/u_resolution.y)) * 0;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, -1/u_resolution.y)) * 0;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)) * 0;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)) * -1/2;
Gx += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)) * 0;
Gx *= adj.x;
Gx.a = 1.0f;
fragColor1 = TDOutputSwizzle(Gx);
//sobel Gy
Gy += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)) * 0;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)) * 0;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)) * 0;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)) * -1/2;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 0/u_resolution.y)) * 0;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, -1/u_resolution.y)) * 1/2;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)) * 0;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)) * 0;
Gy += texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)) * 0;
Gy *= adj.y;
Gy.a = 1.0f;
fragColor2 = TDOutputSwizzle(Gy);
}

uniform vec2 u_resolution;
// uniform vec2 sigma;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float atan2(float y, float x){
const float PI = 3.141592653589793;
return x == 0.0 ? sign(y)*PI/2 : atan(y, x);
}
vec4 atan2(vec4 y, vec4 x){
const float PI = 3.141592653589793;
float r = x.x == 0.0 ? sign(y.x)*PI/2 : atan(y.x, x.x);
float g = x.y == 0.0 ? sign(y.y)*PI/2 : atan(y.y, x.y);
float b = x.z == 0.0 ? sign(y.z)*PI/2 : atan(y.z, x.z);
float a = x.w == 0.0 ? sign(y.w)*PI/2 : atan(y.w, x.w);
return vec4(r,g,b,a);
}
void main()
{
vec4 M = vec4(0.0f);
// vec4 weight = vec4(0.0f);
vec4 O = vec4(0.0f);
vec4 Gx = texture(sTD2DInputs[0], vUV.st);
vec4 Gy = texture(sTD2DInputs[1], vUV.st);
// int filterSize = 4;
//sobel Gx
// M = sqrt(pow(Gx, vec4(2.0f)) + pow(Gy, vec4(2.0f)));
M = vec4(sqrt(Gx.r * Gx.r + Gy.r * Gy.r), sqrt(Gx.g * Gx.g + Gy.g * Gy.g), sqrt(Gx.b * Gx.b + Gy.b * Gy.b), sqrt(Gx.a * Gx.a + Gy.a * Gy.a));
O = atan2(Gy, Gx) * (180/ M_PI);//度数法に変換
// atanの仕様
// https://thebookofshaders.com/glossary/?search=atan
// Gx *= adj.x;
//
// Gx.a = 1.0f;
fragColor1 = TDOutputSwizzle(M);
fragColor2 = TDOutputSwizzle(O);
}
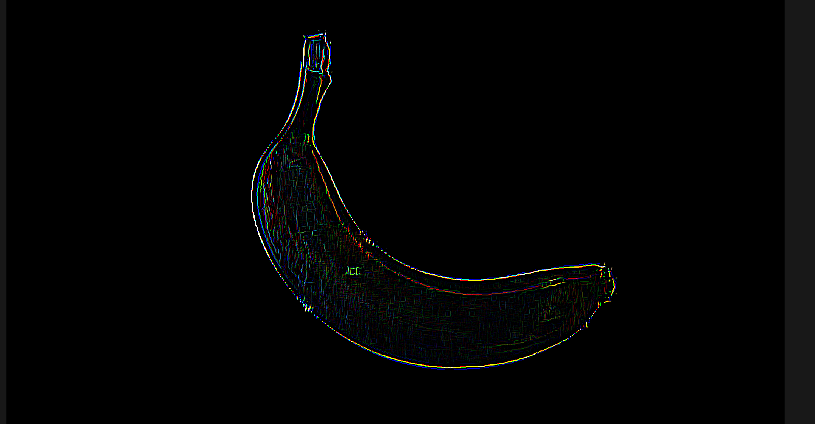
幅が、1pxになっている

uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
// uniform vec2 sigma;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float atan2(float y, float x){
const float PI = 3.141592653589793;
return x == 0.0 ? sign(y)*PI/2 : atan(y, x);
}
vec4 atan2(vec4 y, vec4 x){
const float PI = 3.141592653589793;
float r = x.x == 0.0 ? sign(y.x)*PI/2 : atan(y.x, x.x);
float g = x.y == 0.0 ? sign(y.y)*PI/2 : atan(y.y, x.y);
float b = x.z == 0.0 ? sign(y.z)*PI/2 : atan(y.z, x.z);
float a = x.w == 0.0 ? sign(y.w)*PI/2 : atan(y.w, x.w);
return vec4(r,g,b,a);
}
//
//https://algorithm.joho.info/programming/python/opencv-canny-edge-detecte-py/
float non_max_sup_1(float orientation){
float discreate_orientation = 0.0f;
// 勾配方向を4方向(垂直・水平・斜め右上・斜め左上)に近似
if(
(orientation >= -22.5 && orientation < 22.5) ||
(orientation >= 157.5 && orientation <= 180) ||
(orientation >= -180 && orientation < -157.5)
){
discreate_orientation = 0.0f;
}
else if(
(orientation >= 22.5 && orientation < 67.5) ||
(orientation >= -157.5 && orientation < -112.5)
){
discreate_orientation = 45.0f;
}
else if(
(orientation >= 67.5 && orientation < 112.5) ||
(orientation >= -112.5 && orientation < -67.5)
){
discreate_orientation = 90.0f;
}
else if(
(orientation >= 112.5 && orientation < 157.5) ||
(orientation >= -67.5 && orientation <= -22.5)
){
discreate_orientation = 135.0f;
}
return discreate_orientation;
}
void main()
{
// vec4 weight = vec4(0.0f);
vec4 M = texture(sTD2DInputs[0], vUV.st);
vec4 M_10 = texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0));
vec4 M_m10 = texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0));
vec4 M_11 = texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y));
vec4 M_m1m1 = texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y));
vec4 M_01 = texture(sTD2DInputs[0], vUV.st + vec2(0, 1/u_resolution.y));
vec4 M_0m1 = texture(sTD2DInputs[0], vUV.st + vec2(0, -1/u_resolution.y));
vec4 M_1m1 = texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y));
vec4 M_m11 = texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y));
vec4 O = texture(sTD2DInputs[1], vUV.st);
vec4 NMS =texture(sTD2DInputs[0], vUV.st);
// rch
if(non_max_sup_1(O.r) == 0.0f){
if ((M.r < M_10.r) || (M.r < M_m10.r)){
NMS.r = 0.0f;
}
}
else if(non_max_sup_1(O.r) == 45.0f){
if ((M.r < M_11.r) || (M.r < M_m1m1.r)){
NMS.r = 0.0f;
}
}
else if(non_max_sup_1(O.r) == 90.0f){
if((M.r < M_01.r) || (M.r < M_0m1.r)){
NMS.r = 0.0f;
}
}
else if(non_max_sup_1(O.r) == 135.0f){
if ((M.r < M_1m1.r) || (M.r < M_m11.r)){
NMS.r = 0.0f;
}
}
//g ch
if(non_max_sup_1(O.g) == 0.0f){
if((M.g < M_10.g) || (M.g < M_m10.g)){
NMS.g = 0.0f;
}
}
else if(non_max_sup_1(O.g) == 45.0f){
if ((M.g < M_11.g) || (M.g < M_m1m1.g)){
NMS.g = 0.0f;
}
}
else if(non_max_sup_1(O.g) == 90.0f){
if ((M.g < M_01.g) || (M.g < M_0m1.g)){
NMS.g = 0.0f;
}
}
else if(non_max_sup_1(O.g) == 135.0f){
if ((M.g < M_1m1.g) || (M.g < M_m11.g)){
NMS.g = 0.0f;
}
}
//b ch
if(non_max_sup_1(O.b) == 0.0f){
if ((M.b < M_10.b) || (M.b < M_m10.b)){
NMS.b = 0.0f;
}
}
else if(non_max_sup_1(O.b) == 45.0f){
if ((M.b < M_11.b) || (M.b < M_m1m1.b)){
NMS.b = 0.0f;
}
}
else if(non_max_sup_1(O.b) == 90.0f){
if ((M.b < M_01.b) || (M.b < M_0m1.b)){
NMS.b = 0.0f;
}
}
else if(non_max_sup_1(O.b) == 135.0f){
if ((M.b < M_1m1.b) || (M.b < M_m11.b)){
NMS.b = 0.0f;
}
}
//a ch
if(non_max_sup_1(O.a) == 0.0f){
if ((M.a < M_10.a) || (M.a < M_m10.a)){
NMS.a = 0.0f;
}
}
else if(non_max_sup_1(O.a) == 45.0f){
if ((M.a < M_11.a) || (M.a < M_m1m1.a)){
NMS.a = 0.0f;
}
}
else if(non_max_sup_1(O.a) == 90.0f){
if ((M.a < M_01.a) || (M.a < M_0m1.a)){
NMS.a = 0.0f;
}
}
else if(non_max_sup_1(O.a) == 135.0f){
if ((M.a < M_1m1.a) || (M.a < M_m11.a)){
NMS.a = 0.0f;
}
}
NMS *= adj.x;
//
// Gx.a = 1.0f;
fragColor1 = TDOutputSwizzle(NMS);
// fragColor2 = TDOutputSwizzle(O);
}
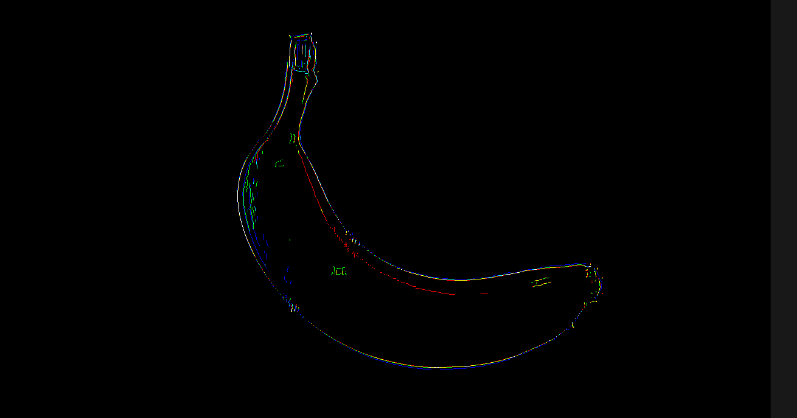
概ね連続している部分のみになった。
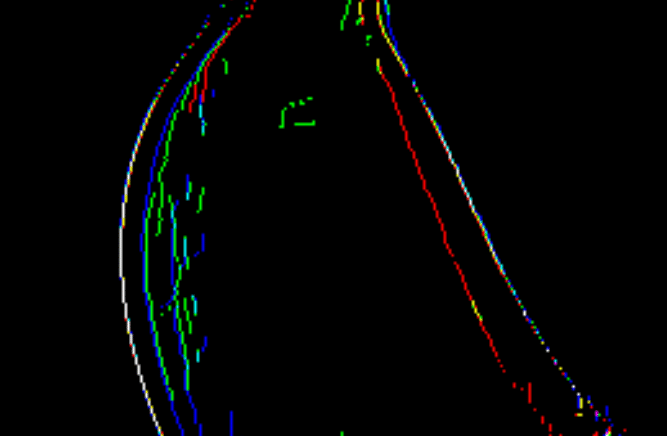
uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
uniform vec2 lambda;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float atan2(float y, float x){
const float PI = 3.141592653589793;
return x == 0.0 ? sign(y)*PI/2 : atan(y, x);
}
vec4 atan2(vec4 y, vec4 x){
const float PI = 3.141592653589793;
float r = x.x == 0.0 ? sign(y.x)*PI/2 : atan(y.x, x.x);
float g = x.y == 0.0 ? sign(y.y)*PI/2 : atan(y.y, x.y);
float b = x.z == 0.0 ? sign(y.z)*PI/2 : atan(y.z, x.z);
float a = x.w == 0.0 ? sign(y.w)*PI/2 : atan(y.w, x.w);
return vec4(r,g,b,a);
}
vec4 hysteresis_threshold(vec4 src, float lambda_low, float lambda_high){
vec4 dest;
//r ch
//最大閾値より大きければ信頼性の高い輪郭
if(src.r > lambda_high){
dest.r = 1.0f;
}
//最小閾値より小さければ信頼性の低い輪郭(除去)
else if(src.r < lambda_low){
dest.r = 0.0f;
}
//最小閾値~最大閾値の間なら、近傍に信頼性の高い輪郭が1つでもあれば輪郭と判定、無ければ除去
else{
bool b = false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-0/u_resolution.x, -1/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)).r >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)).r >= lambda_high) ? true : false;
if(b){
dest.r = 1.0f;
}
else{
dest.r = 0.0f;
}
}
//g ch
//最大閾値より大きければ信頼性の高い輪郭
if(src.g > lambda_high){
dest.g = 1.0f;
}
//最小閾値より小さければ信頼性の低い輪郭(除去)
else if(src.g < lambda_low){
dest.g = 0.0f;
}
//最小閾値~最大閾値の間なら、近傍に信頼性の高い輪郭が1つでもあれば輪郭と判定、無ければ除去
else{
bool b = false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-0/u_resolution.x, -1/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)).g >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)).g >= lambda_high) ? true : false;
if(b){
dest.g = 1.0f;
}
else{
dest.g = 0.0f;
}
}
//b ch
//最大閾値より大きければ信頼性の高い輪郭
if(src.b > lambda_high){
dest.b = 1.0f;
}
//最小閾値より小さければ信頼性の低い輪郭(除去)
else if(src.b < lambda_low){
dest.b = 0.0f;
}
//最小閾値~最大閾値の間なら、近傍に信頼性の高い輪郭が1つでもあれば輪郭と判定、無ければ除去
else{
bool b = false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-0/u_resolution.x, -1/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)).b >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)).b >= lambda_high) ? true : false;
if(b){
dest.b = 1.0f;
}
else{
dest.b = 0.0f;
}
}
//a ch
//最大閾値より大きければ信頼性の高い輪郭
if(src.a > lambda_high){
dest.a = 1.0f;
}
//最小閾値より小さければ信頼性の低い輪郭(除去)
else if(src.a < lambda_low){
dest.a = 0.0f;
}
//最小閾値~最大閾値の間なら、近傍に信頼性の高い輪郭が1つでもあれば輪郭と判定、無ければ除去
else{
bool b = false;
// b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, -1/u_resolution.y)).a >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-0/u_resolution.x, -1/u_resolution.y)).a >= lambda_high) ? true : false;
// b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, -1/u_resolution.y)).a >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 0/u_resolution.y)).a >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 0/u_resolution.y)).a >= lambda_high) ? true : false;
// b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(-1/u_resolution.x, 1/u_resolution.y)).a >= lambda_high) ? true : false;
b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(0/u_resolution.x, 1/u_resolution.y)).a >= lambda_high) ? true : false;
// b = (b == true)|| (texture(sTD2DInputs[0], vUV.st + vec2(1/u_resolution.x, 1/u_resolution.y)).a >= lambda_high) ? true : false;
if(b){
dest.a = 1.0f;
}
else{
dest.a = 0.0f;
}
}
return dest;
}
void main()
{
// vec4 weight = vec4(0.0f);
vec4 I = texture(sTD2DInputs[0], vUV.st);
vec4 canny = hysteresis_threshold(I, lambda.x, lambda.y);
canny *= adj.x;
//
canny.a = 1.0f;
fragColor1 = TDOutputSwizzle(canny);
// fragColor2 = TDOutputSwizzle(O);
}


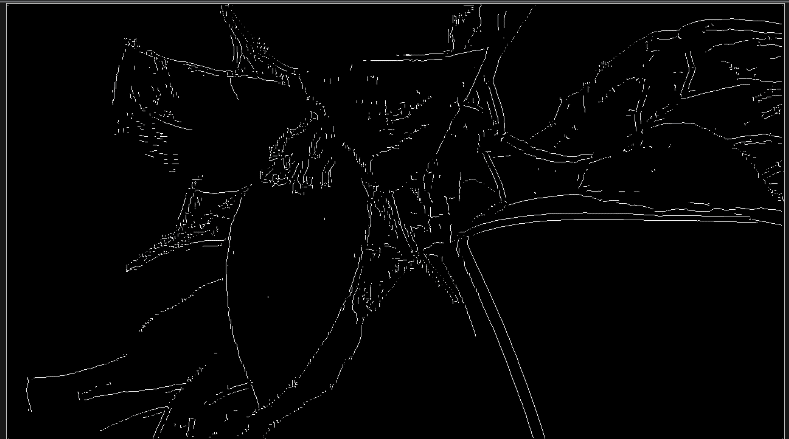
先鋭化
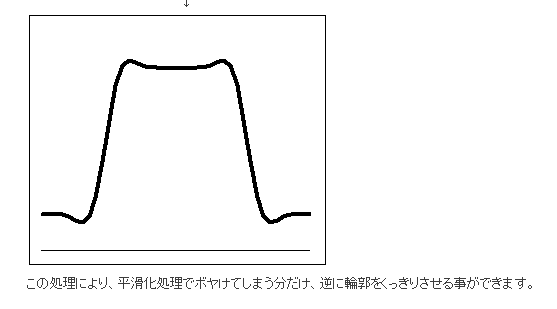
元の画像の濃淡を残したままエッジを強調sるうことで、いわゆるシャープネスを上げるような処理について先鋭化(sharpening)という。
アンシャープマスキング
unsharp masking
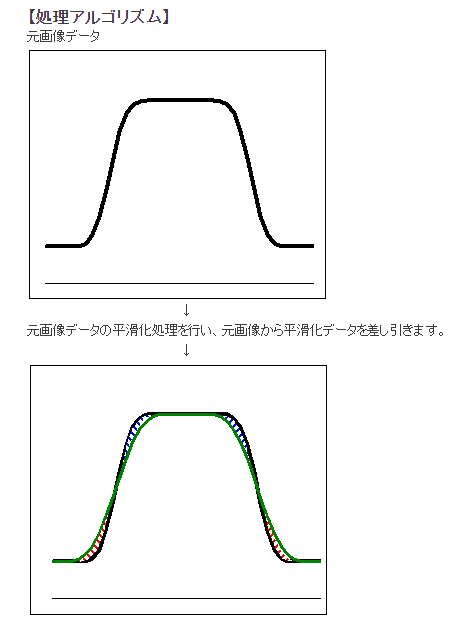
入力画像に対して、平滑化処理を施し、その結果を元の画像から引くことにより、元の画像からエッジの部分が取り出されたような画像が得られる。
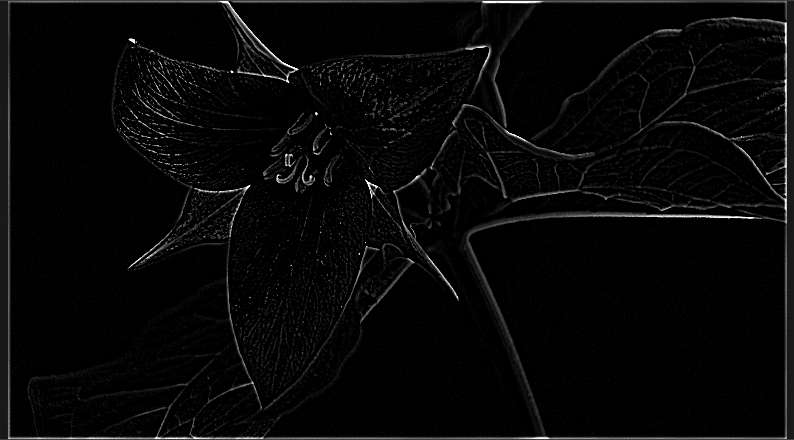
この時点では、減算したものには+/-の成分がある。
uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
uniform vec2 sigma;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float gauss(float x, float y, float sigma){
float exponent = - (x * x + y * y) / (2 * sigma * sigma);
float denominator = 2 * M_PI * sigma * sigma;
return exp(exponent) / denominator;
}
vec4 grayscale709(vec4 src){
vec3 gray709 = vec3(0.2126, 0.7152, 0.0722);
float lum = dot(src.rgb, gray709);
return vec4(lum, lum, lum, src.a);
}
void main()
{
vec4 G = vec4(0.0f);
vec4 weight = vec4(0.0f);
vec4 original = texture(sTD2DInputs[0], vUV.st);
vec4 fc = vec4(0.0f);
int filterSize = 4;
//gauss
for(int i = -filterSize; i <= filterSize; i++){
for(int j = - filterSize; j <= filterSize; j++){
G += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y)) *gauss(i, j, sigma.x);
weight += gauss(i, j, sigma.x);
}
}
G /= weight;
fc = grayscale709(original) - grayscale709(G);
if(fc.r > 0.0f){
fc = vec4(fc.r, fc.g, 0.0f, fc.a);
}
else if(fc.r < 0.0f){
fc = vec4(0.0f, -fc.g, -fc.b, fc.a);
}
fc *= adj.x;
fc.a = 1.0f;
fragColor1 = TDOutputSwizzle(fc);
}

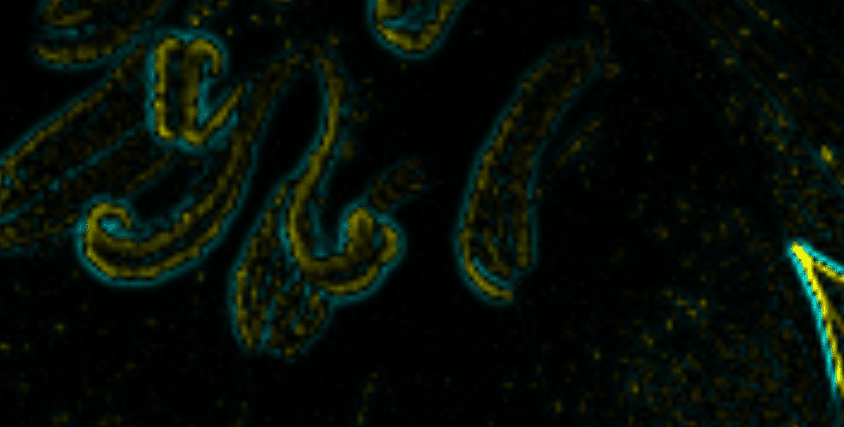
そうして、このエッジ画像を元の画像と足し合わせることにより、画像のエッジが強調された(先鋭化された)画像が得られる。
このエッジ画像に定数倍の調整変数をつけると、どのくらいエッジを強調するかをコントロールできる。



uniform vec2 u_resolution;
// uniform vec2 sigma;
uniform vec3 adj;
uniform vec2 sigma;
// out vec4 fragColor;
layout(location = 0) out vec4 fragColor1;
layout(location = 1) out vec4 fragColor2;
layout(location = 2) out vec4 fragColor3;
#define M_PI 3.1415926535897932384626433832795
float gauss(float x, float y, float sigma){
float exponent = - (x * x + y * y) / (2 * sigma * sigma);
float denominator = 2 * M_PI * sigma * sigma;
return exp(exponent) / denominator;
}
vec4 grayscale709(vec4 src){
vec3 gray709 = vec3(0.2126, 0.7152, 0.0722);
float lum = dot(src.rgb, gray709);
return vec4(lum, lum, lum, src.a);
}
void main()
{
vec4 G = vec4(0.0f);
vec4 weight = vec4(0.0f);
vec4 original = texture(sTD2DInputs[0], vUV.st);
vec4 fc = vec4(0.0f);
int filterSize = 4;
//gauss
for(int i = -filterSize; i <= filterSize; i++){
for(int j = - filterSize; j <= filterSize; j++){
G += texture(sTD2DInputs[0], vUV.st + vec2(i/u_resolution.x, j/u_resolution.y)) *gauss(i, j, sigma.x);
weight += gauss(i, j, sigma.x);
}
}
G /= weight;
fc = grayscale709(original) - grayscale709(G);
fc *= adj.x;
fc = original + fc;
// if(fc.r > 0.0f){
// fc = vec4(fc.r, fc.g, 0.0f, fc.a);
// }
// else if(fc.r < 0.0f){
//
// fc = vec4(0.0f, -fc.g, -fc.b, fc.a);
// }
fc *= adj.y;
fc.a = 1.0f;
fragColor1 = TDOutputSwizzle(fc);
fragColor2 = TDOutputSwizzle(original);
}
フィルタとしてあらわすと、以下のようなフィルタが等価になる。このようなフィルタを先鋭化フィルタ(sharpening filter)と呼ばれている。
$${k=9}$$のときは綺麗な整数倍になる。kの値を大きくしていくことで先鋭化の強さが強まる。
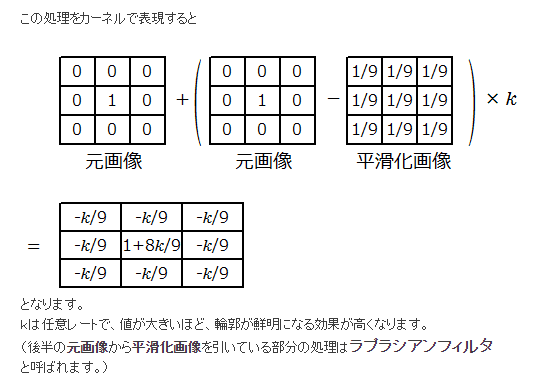
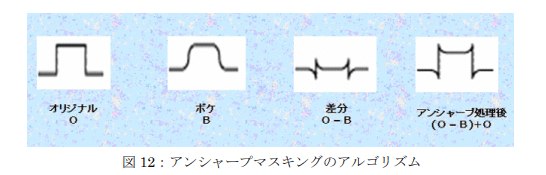
元々はフィルム写真の暗室技術で、ぼかした画像をマスクとして使用したことに由来される。
その他の非線形フィルタ
周波数フィルタリング
以上のように考えた時、画像は周波数の組み合わせで構成されているといえるでしょう。信号処理などの分野では、信号にどのような周波数が含まれるのか解析する目的で、フーリエ変換が用いられます。
画像処理においても同様にフーリエ変換を用いた解析を行うことで、画像を周波数領域の関数で表現することができます。すなわち、どのような周波数の波が画像に含まれているのかを解析することができるのです。
画像を2 次元空間の関数f(x, y) として表すとき、フーリエ変換F(u, v) は以下のように定義されます。
画像における周波数成分というのは基本的には空間周波数というものを考えている。
空間周波数
音声信号のような時間的に変化する信号は、1 秒間あたりに変化する波の数を「周波数」と表します。画像では、位置によって(空間的に)明るさ(信号)が変化しています。このような空間的に変化する信号の周波数を「空間周波数」といいます。
補間フィルタ
画像を拡大・縮小・回転など、何かしらの目的の際に、元の画像には存在しなかったピクセルを補間しないといけない場合のフィルタについて。
主によく使われるのは画像のリサイズの際の補間に使われるケースが多い。
Lutファイルの補間にも使用される。
最近傍補間・ニアレストネイバー
Nearest neighbor interpolationhttps://en.wikipedia.org/wiki/Nearest-neighbor_interpolation
エッジ保存スムージングの項にて、k最近隣平均化フィルタ(k-nearest neighbor averaging filter)があったが、概念としては似たようなもので、その平均化の作業を行っていないようなイメージ。
一番シンプルな手法。
リサイズの際のNearest Neighborを考えてみる。
元画像の画素値を$${f(x,y)}$$とし、拡大率を$${s}$$、出力画素値を$${g(x,y)}$$とすると、下記のようになる。
$$
g(x,y) = f(\frac{x}{s}, \frac{y}{s})
$$
拡大・縮小後の座標値(x,y)はsで除算すると、非整数値となるため、四捨五入などをし、最近傍となる座標を出力画素値とする。
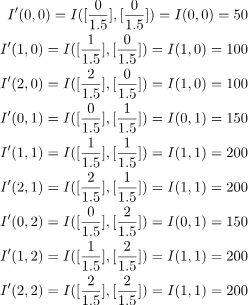
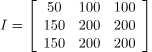
回転処理を考えてみる。
角度$${\theta(rad)}$$で、回転後の座標を$${(x', y')}$$とすると、回転行列より、以下のように表せれる。
$$
x' = x\cos\theta - y\sin\theta\\
y' = x\sin\theta + y\cos\theta
$$
リサイズ同様に非整数座標ではダメなため、回転後の座標値$${(x',y')}$$を四捨五入して最近傍の座標を取得し、それを出力画素値とする。
、
双一次補間・バイリニア法
Bilinear interpolation
周囲の4つの画素を用いた補間方法。
Nearest Neighborよりは処理が重いが、画質はおおむね向上する。
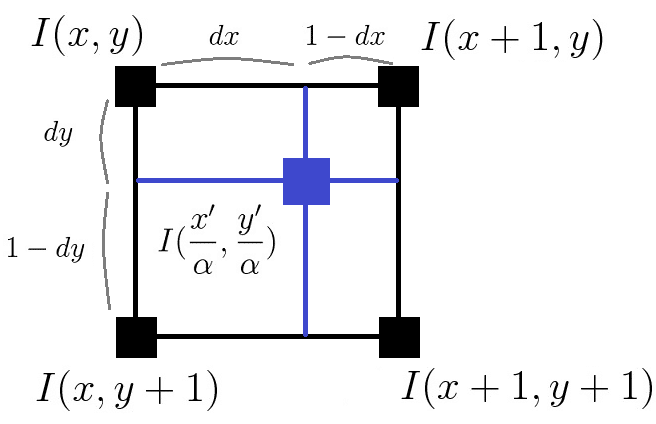
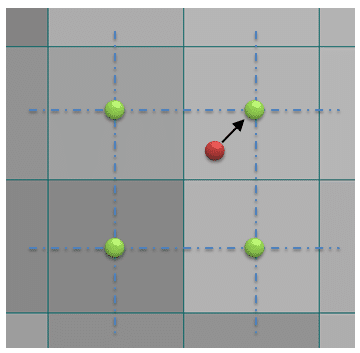
例えば、リサイズ・回転処理などを考えてみる。リサイズ・回転処理の結果上記の画像の青い地点に位置したとする。
$${I(x,y), I(x+1, y), I(x, y+1), I(x+1, y+1)}$$は元画像における座標位置とする。
$${I(x,y)}$$を基準にそこまでの距離を$${dx, dy}$$とする。
元画像の周辺4画素からの距離が近ければ近いほど、大きく重みづけするような処理を行って画素値を決定させる。
それぞれ周辺4がそとの距離を求める。距離によって重みづけを(0-1)で行う。
最終的に周辺四画素からの加重平均を取ったものを出力画素値とする。
$$
I'(x', y') = (1-dx)(1-dy)I(x,y) + dx(1-dy)I(x+1, y) +(1-dx)dyI(x, y+1) + dxdyI(x+1, y+1)
$$
双三次補間・バイキュービック法
Bicubic interpolation
Lanczos
ランチョス
Reference
画像フィルタ(空間フィルタリング)による画像処理検査 | ヴィスコ・テクノロジーズ株式会社
画像フィルタ(周波数フィルタリング)による画像処理検査 | ヴィスコ・テクノロジーズ株式会社
空間フィルタ処理 – blog|メディア情報研究室|村上真研究室|東洋大学総合情報学部
画像のフィルタリング処理 PDF
画像リサイズ処理のうんちく - Qiita
画像リサイズのうんちく (補間フィルタ) - Qiita
