
新NISAの日本株式市場へのインパクトをシミュレーションしてみた
はじめに
新NISAが2024年1月から始まり、年間投資枠360万円(つみたて投資枠120万円+成長投資枠240万円)までの投資信託や株やETF等への投資に対し、売却益や分配金や配当金に対する税20.315%(所得税+住民税+復興特別所得税)が非課税になります。
実際、2024年年初から日経平均株価が上昇しているなど、株式市場は活況のスタートとなりました。
また、全世界株式(オール・カントリー、通称オルカン)の月間積立予約が2000億円規模になったとのニュースもありました。
東証プライム市場の時価総額は現在およそ890兆円なので、年間にして0.27%のインパクトがある投資規模とも言えます。
これだけインデックスファンドに大量の資金が投入すると、株価にどのような影響を与えるのでしょうか?
そこで、今回は、積立型インデックスファンドによる株式市場への影響についてシミュレーションをしてみました。
モデルの前提
NISAの積み立て投資は長期保有が前提と考えられるため、一度保持したら長期間売却されないものとします。
また、株価は買い需要と売り供給のバランスによって決まるものとします。
また、発行株数の総数は一定とし、流動性のある株と固定保有された株のうち、流動性のある株のみが売りに出されるものとします。売り供給は流動株のうち毎月あるランダムな割合で売りに出されるものとします。
買い需要は発行株数のうち毎月あるランダムな割合で買い求められる分と、インデックスファンドによる積立需要分の合計とします。インデックスファンドによる積立需要は、発行株数に対して一定の割合のケース(ケース1)と、毎月一定の金額分のケース(ケース2)を想定します。
評価損益は、その時点での保有株の時価とそれまでに購入に要した投資額との差で求めます。金利は考慮していません。
また、ファンドの配当金分の損益や配当金の再投資する場合などは、ここでは考慮していません。
数式モデル
数式モデルを立てるにあたって以下の記号を導入します。
まず、株数について、流動株数、固定株数、発行株数、株価を導入します。

次に売買需給について、売り供給株数、買い需要株数と関連する係数を導入します。
売り供給株数と市場買い需要は流動株分のみで売買されるものとします。
一方で、積立買い需要は流動株数ではなく発行株数に応じて決まるものとします。

売り供給係数は0から最大値の間での一様乱数を仮定します。
市場買い需要係数は0から最大値の間での一様乱数を仮定します。
積立買い需要係数はケース1(株数一定)とケース2(金額一定)の2パターンを想定します。

このとき、市場の変化をシミュレーションする差分方程式を定義します。

積立買い需要分は固定株数としてカウントされます。固定株数が増える分は流動株数が減少します。
価格pは、需給バランスに対してある弾力性係数aに応じて変動するものとします。
また、パラメータの初期値を以下のように設定します。
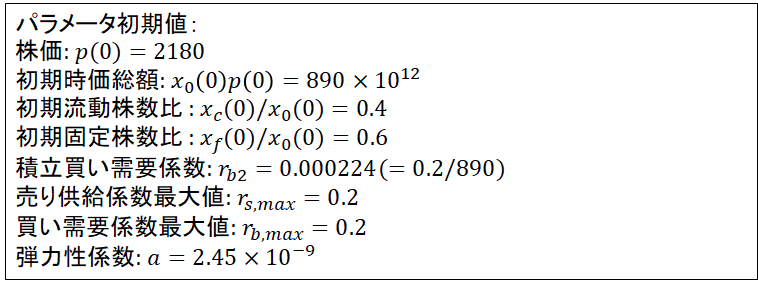
初期株価(1株当たり時価)は現在の東証プライム株価を参考に2180円とします。
初期時価総額は現在の東証プライム時価総額を参考に893兆円とします。
積立買い需要係数は毎月2000億円の積立があるものと仮定します。
流動株比率を仮に40%とします。これは東証プライムの上場基準が流動株の比率が35%以上であることを要請しているためです。
以下のページを参考にしました。
ケース1とケース2の意味
ケース1は株数一定です。これは、市場ポートフォリオが時価総額に応じた加重平均で求められることに対応しています。
例えば、A社株とB社株の保有株数をそれぞれxA, xBとし、株価をpA, pBとすると、保有割合はxA : xBですが、時価総額比はpA xA : pB xBです。
もし、株価が変わらないとして、株数だけそれぞれ一定割合rだけ増加すると、保有割合はxA (1 + r) : xB (1 + r)ですが、時価総額比はpA xA (1+r) : pB xB (1 + r) = pA xA : pB xBで変わりません。
つまり、時価総額に応じた加重平均であるという性質が保たれる訳です。
しかし、株価の変動が生じた場合は金額も変動します。
ケース2は金額一定です。これは、毎月の積立金額が一定であることに対応しています。
しかし、株価が高い株は少なく積み立てられ、株価が安い株は多く積み立てられることになるため、市場ポートフォリオに連動するためには、リバランスが必要になってきます。
計算例
それでは、いくつかの計算例を示していきたいと思います。計算期間は10年(120ヵ月)です。
グラフは3段ありますが、1段目は流動株と発行株の比率、2段目は株価でcase0は積立がない場合、case1はケース1の積立がある場合、case2はケース2の積立がある場合、3段目は評価損益です。横軸の単位は月です。
計算例1(右肩上がり)
株価が順調に右肩上がりしていくという例です。

流動株比率は2~3%低下していきます。
株価に与える影響は殆ど見られません。
評価損益は10年間で4兆円のプラスです。
計算例2(不調)
株式市場の不調が続くという例です。

流動株比率は2~3%低下していきます。
株価に与える影響は数%上振れする程度です。
評価損益は10年間で2兆円のマイナスです。
計算例3(バブル崩壊)
途中まで調子が良い状態が続いて突然バブルが崩壊する例です。

流動株比率は2~3%低下していきます。
株価に与える影響は数%上振れする程度です。
評価損益は10年間で1兆円のマイナスです。
計算例4(興味深い)
株価は傾向として右肩上がりですが、興味深い例です。

流動株比率は2~3%低下していきます。
株価に与える影響は軽微です。
評価損益は10年間で0.8兆円のプラスです。
興味深いのは、全体としては株価は上昇傾向であるにも関わらず、72月目付近で評価損益がゼロ付近になっている点です。
これは、当初の右肩上がり付近で積みました結果、60~72月の下落の影響を大きく受けているためです。
単純な積立だと、後半になるにつれ損益は時価の株価に強く影響を受けます。
おわりに
新NISAの株式市場に与える影響をシミュレーションしてみました。
結果として、流動株に比率を2~3%程度低下させる影響が見られました。
ただし、株価に与える影響は軽微のようです。
また、単純な積立では、株価が下振れした場合に、保有株数が増加するにつれ損益が大きな影響を受けます。なので、機械的に積み立てるだけでなく、出口戦略をしっかり考えていく必要がありそうですね。
また、日本の個人投資家はむしろ日本株を売って外国株を買っているという情報も出てきていますが、そのあたりについても今後別記事で検討してみたいと思います。
